Response Theory in Ecosystems
Relatore: Prof. Amos Maritan
Correlatore: Prof. Sandro Azaele
Studente:
Umberto Maria Tomasini
Natura: insieme di ecosistemi
organismi viventi + ambiente
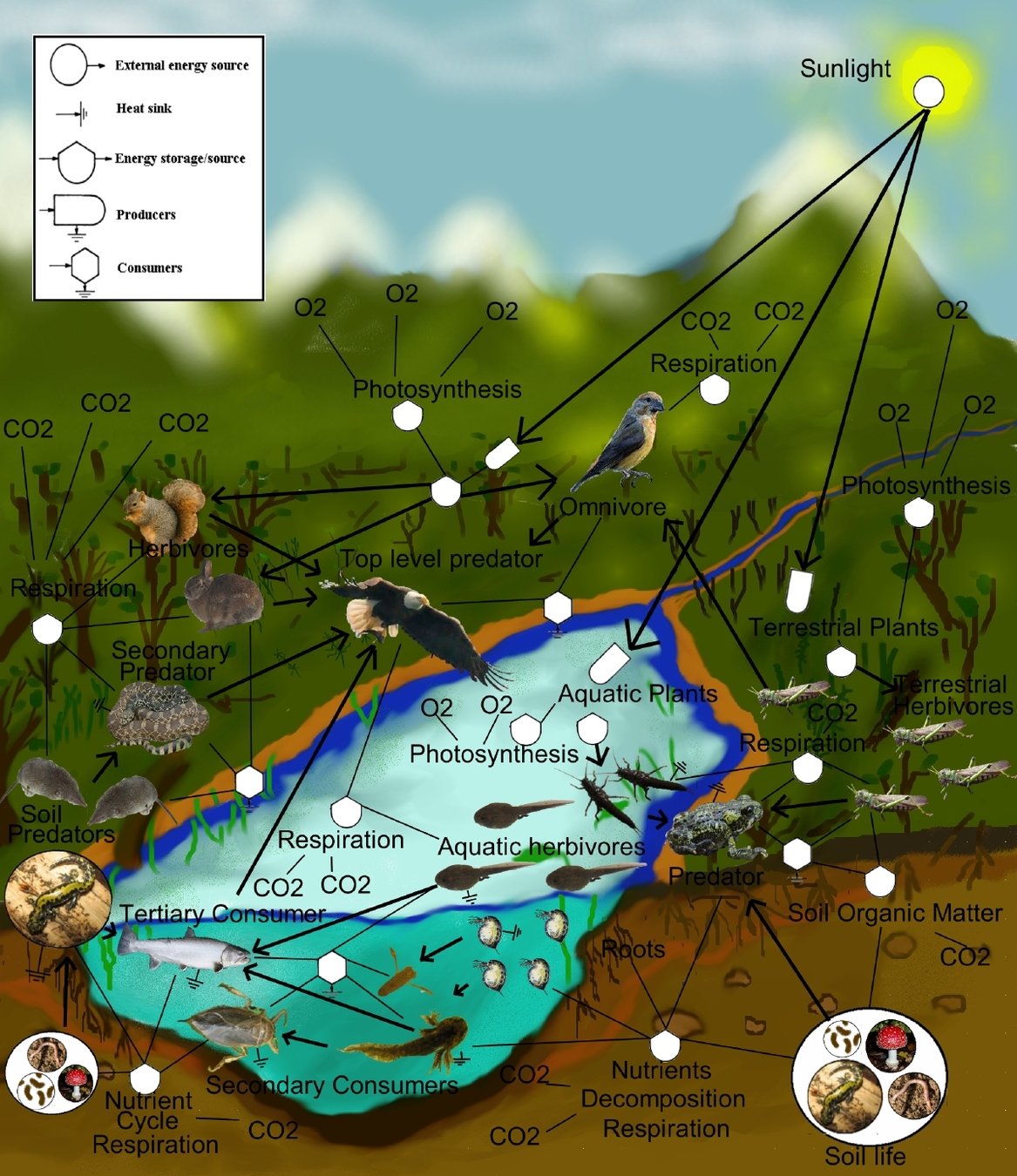
Interazioni fra specie
-
Corta scala temporale
- Predazione (+,-)
-
Lunga scala temporale:
- Mutualismo: (+,+)
- Commensalismo: (0,+)
- Parassitismo: (+,-)
- Competizione (-,-)
Gli ecosistemi sono sistemi complessi!
- Diversi fenomeni interni a diverse scale spazio-temporali
- Interazione con ambiente esterno
Equilibrio di un ecosistema
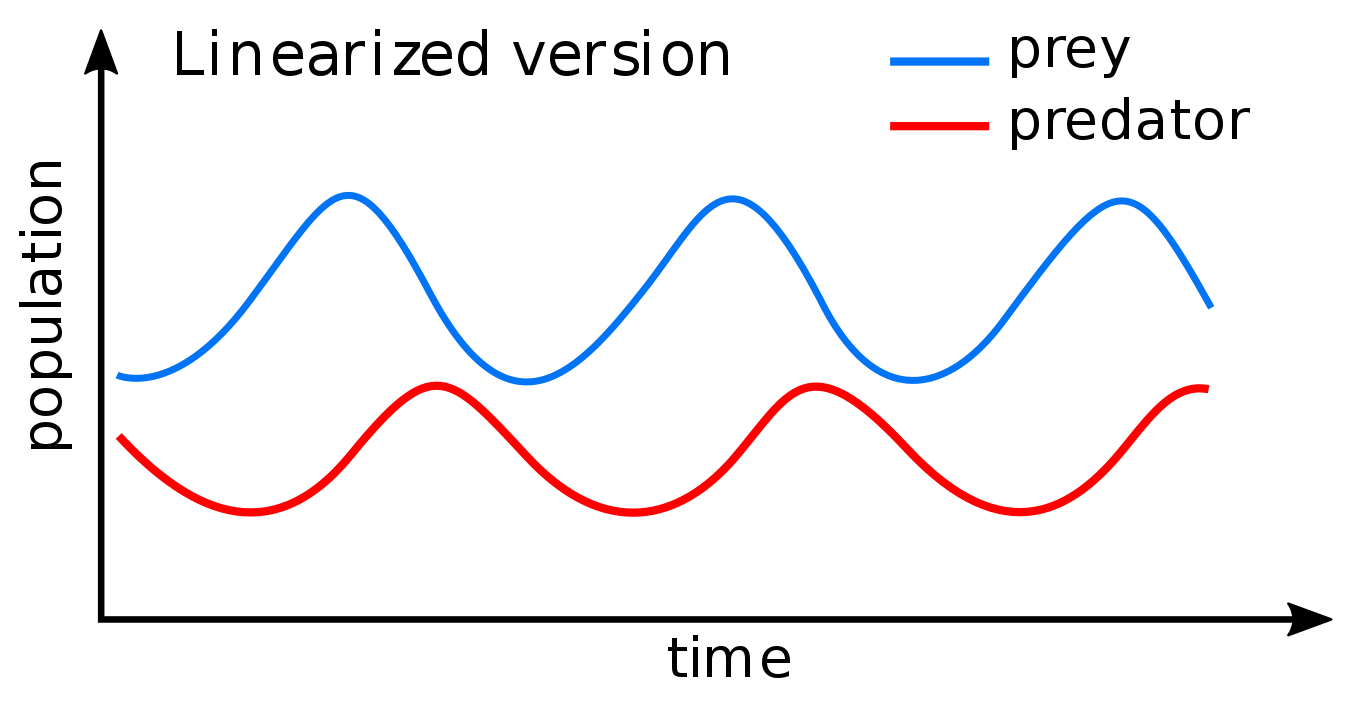
Esempio:
- Preda - Predatore, descritto dal modello di Lotka-Volterra
Equilibrio: questo ciclo continua all'infinito.
Perturbare un ecosistema
Esempi naturali/artificiali:
- Pesca/caccia intensiva
- Volume di pioggia ridotto
- Deforestazione
Due scenari:
- Perturbazione piccola: equilibrio
- Perturbazione grande: estinzione
Capacità dell'ecosistema di tornare all'equilibrio: Resilienza
É possibile predire la risposta dell'ecosistema a una perturbazione?
- Teoria di Fisica Statistica
- Obiettivo: predire il cambio di alcune quantità di interesse dopo aver perturbato il sistema.
- Molte formulazioni ed applicazioni (Ottica, Materiali, Clima).
Teoria della Risposta 1/3
Teoria della Risposta 2/3
\dot{x}(t)= F(x(t))
\dot{x}(t)= F(x(t))\textcolor{blue}{+G(x)e(t)}
\langle A(t)\rangle \approx \langle A(0)\rangle +\textcolor{blue}{\langle \Delta A(t)\rangle}+...
Perturbazione
Risposta
\langle \Delta A(t)\rangle = \textcolor{blue}{R_{A,G}(t)}\ast e(t)
Teoria della Risposta 3/3
- \(\textcolor{blue}{R_{A,G}(t)}\) fornisce la risposta del sistema, data la perturbazione del sistema
- Una volta ottenuta \(\textcolor{blue}{R_{A,G}(t)}\): predizione del sistema a diverse \(e(t)\)
Un modello per ecosistemi
\(\dot{x}= b-\frac{x(t)}{\tau}+D\sqrt{(x+\frac{1}{\mu}x^2)}\xi(t)\)
Immigrazione di nuove specie
Ecosistemi:
in equilibrio fra estinzione e "iper-robustezza"
Un modello per ecosistemi
\(\dot{x}= b-\frac{x(t)}{\tau}+D\sqrt{(x+\frac{1}{\mu}x^2)}\xi(t)\)
Morte di individui
Ecosistemi:
in equilibrio fra estinzione e "iper-robustezza"
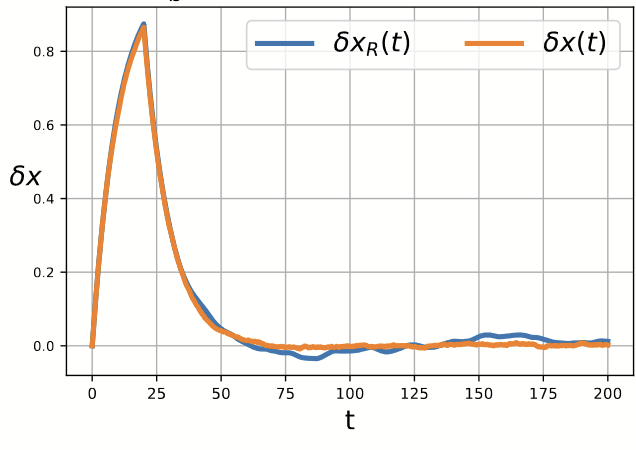
Se cambia l'immigrazione?
Predizione
\(b\rightarrow b+\textcolor{blue}{G e(t)}\)
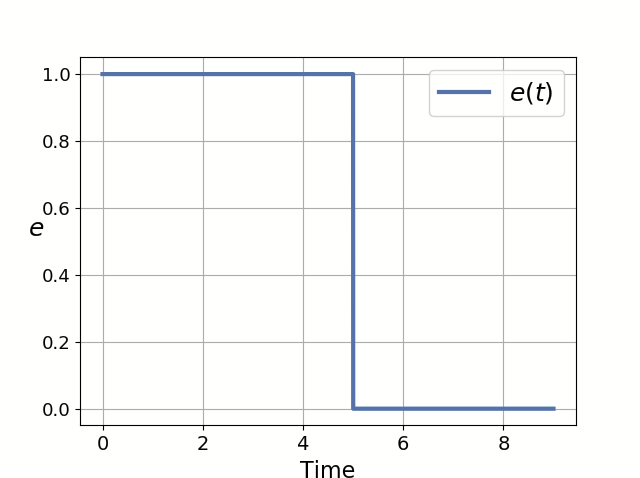
\(2\tau\)
\(G=0.1\)
\(b=1\)
\(\tau=10\)
\(D=0.01\)
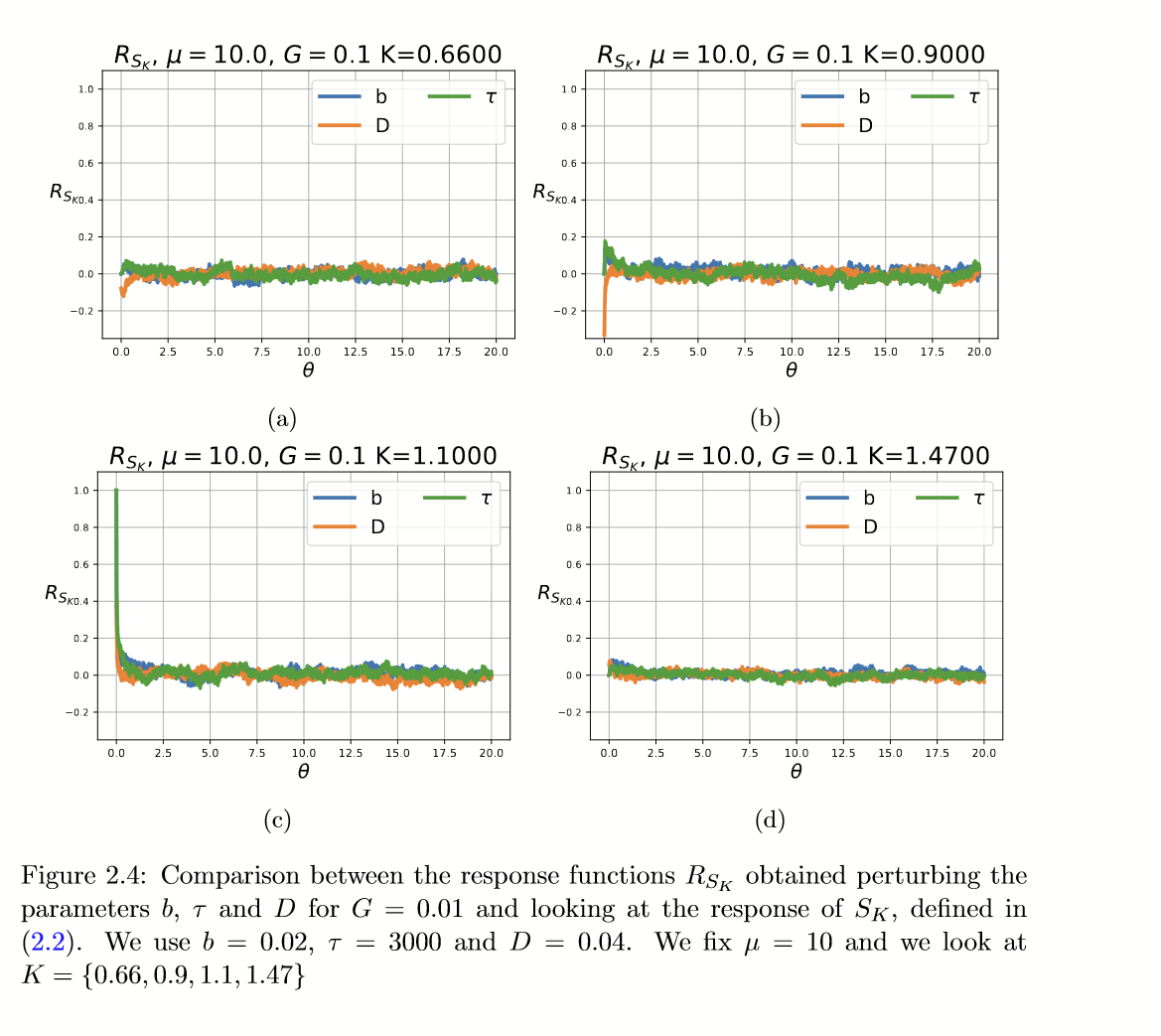
Sensibilità rispetto ai parametri ecologici
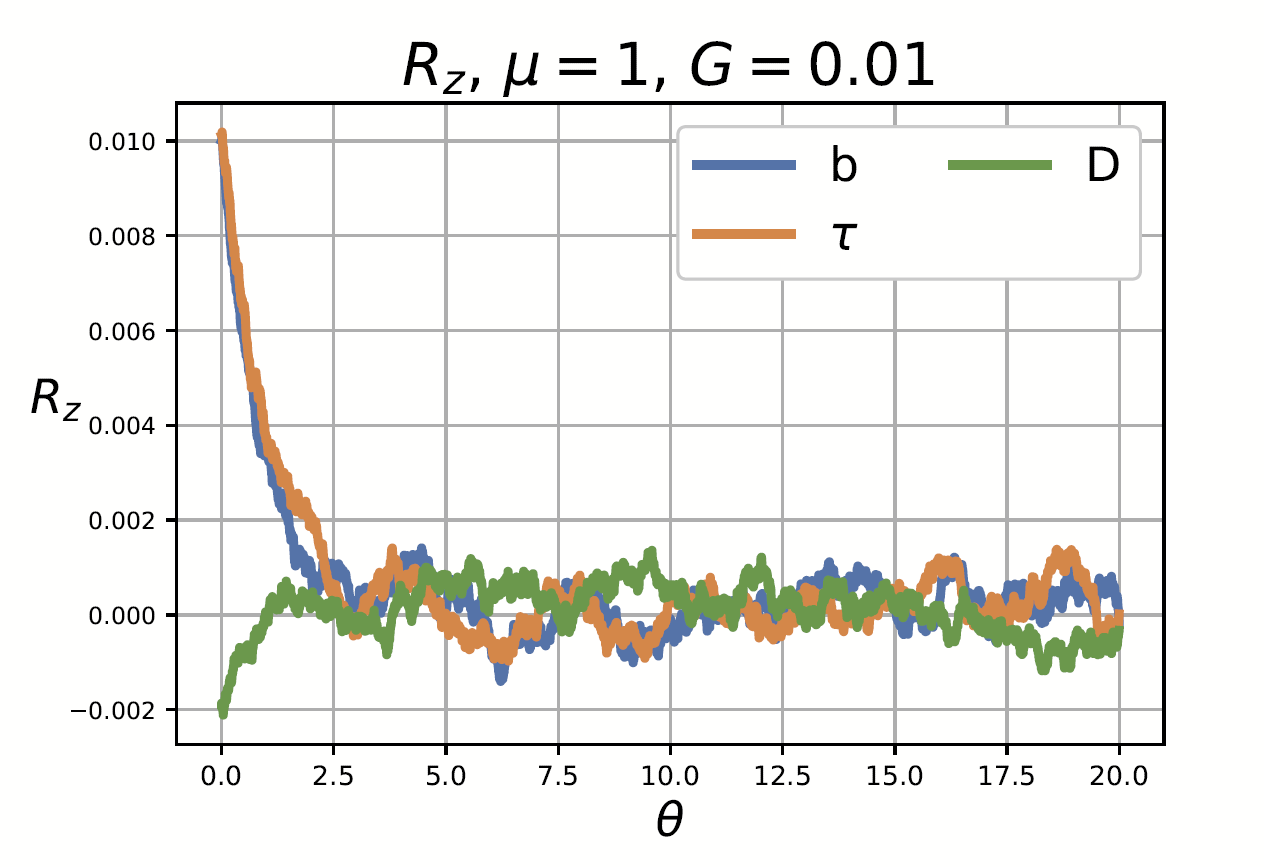
\(G=0.01\)
\(b=1\)
\(\tau=10\)
\(D=0.01\)
Conclusioni:
- Teoria della Risposta per studiare la resilienza degli ecosistemi
- Teoria testata su modelli semplici
Prospettive: Dati reali
-
Paracou dataset:
- Più perturbazioni controllate della foresta (>30 anni)
- La teoria della risposta può predire come cambia la biodiversità?
Grazie per la Vostra attenzione.
BACKUP
R_{A,G}(t)=-\Theta(t) \int d^N x A(x) e^{t L_{FP}^0}\sum_j \partial_j(G_j(x)p_0(x))
Predizioni teoriche 1/2
R_{x,b}=-\Theta(t)\frac{2G_b}{D^2}\left[\frac{1}{\tau} \left\langle\frac{x(t)}{x(0)} \right\rangle-b\left\langle\frac{1}{x(0)} \right\rangle
\right]
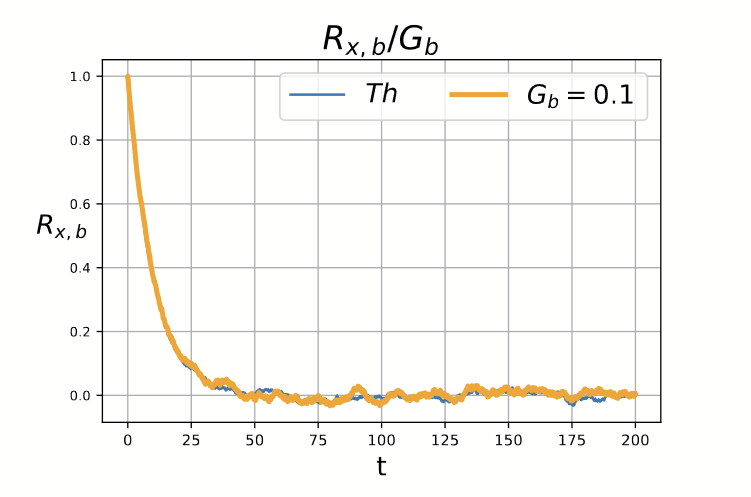
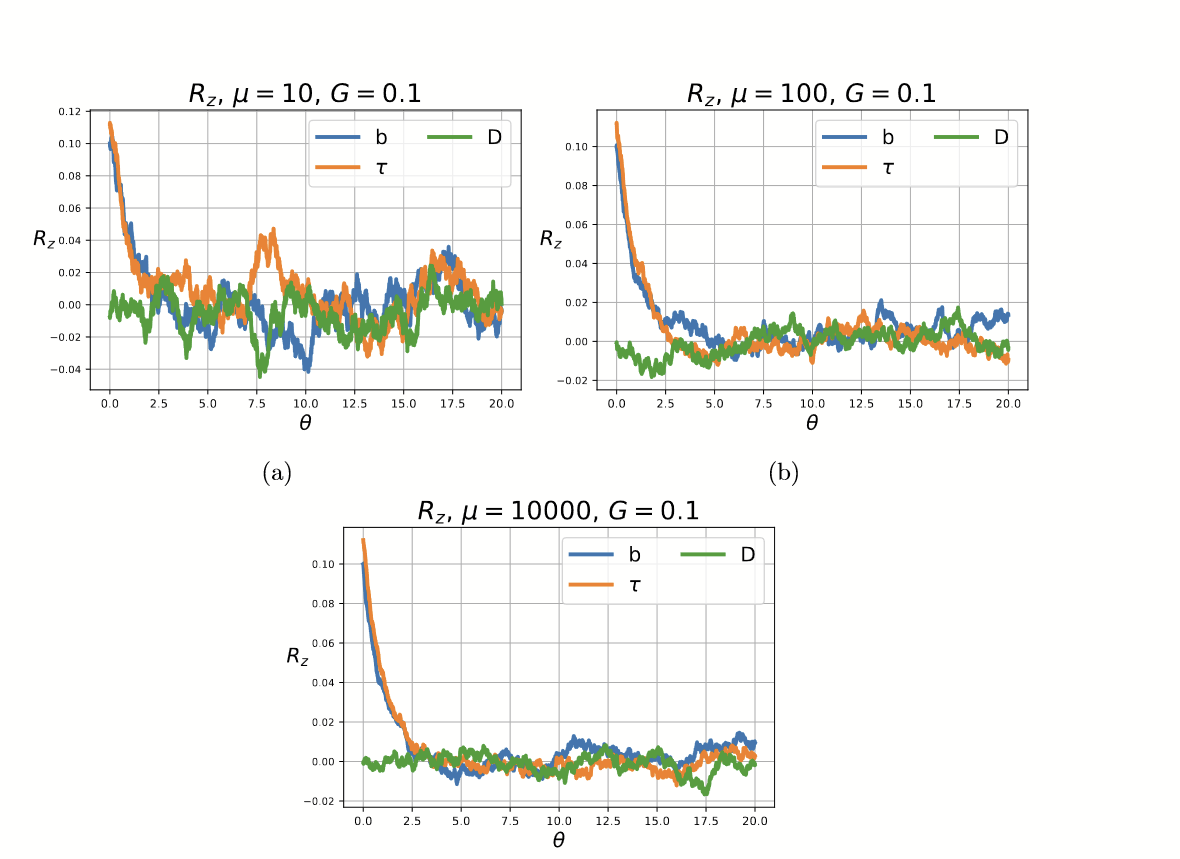
Predizioni teoriche 2/2
\begin{aligned}
R_{x,b}&=\langle \delta x(t) \rangle\\
&=\sum^M_{i=1}\delta x^{(i)}(t)
\end{aligned}
Come ottenere numericamente le funzioni di risposta
S_K = \int_{K}^{\infty}P_{st}(x)dx
Response Theory in Ecosystems
By umberto_tomasini
