Education

Bachelor in Physics (UniPD)
- Thesis on Quantum Mechanics
Master in Physics of Matter (UniPD)
- Thesis on Statistical Physics and Climate models
Supported by Excellence School scholarship

Work Experience

PhD in AI (EPFL):
- Quantify and interpret generalization in Deep Learning
- Research on Protein Design with Diffusion Models
- 5 papers (4 as first author) presented in 12 venues as ICLR and 2 ICML spotlights
Applied Scientist Intern (AWS AI Labs, California)
- Improve Large Language Models for complex reasoning
- One U.S. patent and 1 paper in preparation (first author).

[U.S patent]

Language Models as Theory Solvers

Online Shopping with AI assistant

Working Backwords

Wrong! More than $30, polyester.

Much general problem...

Planning
Calendaring
Storytelling
...

Every time you need an answer with many constraints

Goal: enable LLMs to generate correct answers,
even with many constraints

Formal solvers solve statements with many constraints.

For example finding $x$, $y$, $z$ to solve:

$x*z=y\land(z<0\lor y=0)$

Used in applications as automated theorem proving and software testing.

Many constraints: formal solvers

Query: "I want a pet. Hyena or cat?"

Needs lot of additional information:

$\Rightarrow$needs an extensive ontology.

But also the point of the question is fuzzy, answering needs commonsense.

LLMs already have commonsense grounded in them.

Formal solvers for language is not scalable

Is a hyena legal to keep in the US?
Is a hyena considered a pet?
Is a hyena dangerous?

Method idea: merge LLMs with formal solvers

LLMs: world knowledge for informal reasoning
Formal solvers: logical consistency

1. Formal solver chooses which constraints satisfy, e.g .:
[entree] and [side] are vegetarian. [entree] is heavy. [side] is light.

2. LLM:

[entree] is "Falafel".
[side] is "Salad".

First simplify, then solve

Find vegetarian entree and side.
If the entree is heavy then the side is light.

Query:

Constraint-explicit:

[entree] and [side] are vegetarian.

IF [entree] is heavy THEN [side] is light.

$\rightarrow $ Constraint Satisfiability Problem in NL

Can we reliably use LLMs for Constraint Satisfiability Problems?

For evaluation:

Proposed a new benchmark
Finding a set of $n$ objects which satisfy $m$ constraints in the prompt
Constraints both hard and commonsense

The LLM replies by yielding $n$ items from a list of items $\mathcal{V}$.

Open-weight: is the LLM loss aligned with accuracy?

Prompt: $T_{1, ... ,m} = T(c_1, ... , c_m)$, $c_i(x_1,...,x_n)$

Human: [x_1] and [x_2] are vegetarian. [x_1] is high in calories.

LLM: $\underset{x_1,x_2\in\mathcal{V}}{\min}-\log p(x_1,x_2|T_{1,...,m})$

Answer: [x_1] is "rice".[x_2] is "salad".

Instead of:
Answer: [x_1] is "Falafel". [x_2] is "salad".

Failure can come from relying on spurious correlations between input and pre-training corpus (Token Bias).

Removing Token Bias

$\rightarrow$can be caused by relying on position / value of tokens in the prompt or in the answer

$\rightarrow$ instead of truly answering the question

Solution: to mitigate Token Bias, we reweight the logits $-\log p(x_1,x_2|T_{1,...,m})$

Metric: accuracy of smallest-loss solution $(x_1,x_2)$ over satisfying the $m$ prompt constraints (%)

Results:

Poor base performance $\sim 50\%$.

We can improve by 10-20% (relative terms).

Close-weight models

Stronger models (e.g. Claude)
No loss: just prompt the model!

Constraints (already annotated, can be scaled with LLM):

The sum of the prices for 7 people of [transportation_1][breakfast_1], [lunch_1], [dinner_1], [accommodation_1], ... , [accommodation_3] does not exceed 30,200.

[accommodation_1], [accommodation_2], [accommodation_3] must be suited for 7 people.

TravelPlanner: benchmark for real-world planning

with Language Agents

Query example (challenging):

Could you create a travel plan for 7 people from Ithaca to Charlotte spanning 3 days, from March 8th to March 14th, 2022, with a budget of $30,200?

$\Rightarrow$ LLM replies with travel plan

Metrics: pass rate over satisfying all constraints (%)

Results

Method	Pass rate (%)	Num calls (avg)
Direct prompting	2.8	1
CoT	2.8	1
React	7.8	7
Ours	`7.2`	`2.5`

Method: explicit constraints + self-refinement scheme

$\Rightarrow$ We can improve Claude of more than 200%!

From 3% to 7%, less LLM calls than React

We propose a method to use LLMs as theory solvers for constrained language tasks, in tandem with formal solvers:

A first approximation is zero-shot prompting (black-box models). In TravelPlanner, we go from 2.8% to 7.2%.
For open-source models, we can manipulate the loss to improve consistency with constraints. Removing token bias, we improve 10-20% in relative terms on a toy dataset.

Conclusions

Constrained to problems that can be formalized as constraints over variables. Leaving out e.g. factual queries:
- Is dog an animal?
Relying on the auto-formalization: fine-tuned model.
Future work should implement the full SMT loop, possibly end to end
Using the satisfaction of constraints as reward for RL.

Limitations and Future steps

$x+y =3$

IF $x > 2$:
$y = 0$

1. SAT solver chooses which statements satisfy, e.g . :

$x+y = 3$ AND $x> 2$ AND $y= 0$

2. Theory solver:

$x=3$, $y = 0$

SMT solvers first simplify, then solve

"Find a first and second course without pork meat. The first course should be from Asian cuisine, and the second from Italian cuisine. If the first course is light in calories, the second should be heavy, and vice versa. If the first course is steamed, the second must also be steamed"

Failure:
"Vegetable dumplings (steamed)"
"Eggplant Parmigiana (baked)"

Costumer benefit

Answers more consistent with questions, increasing trust

[Claude 3 Sonnet]

"[first_course] and [second_course] are dishes without pork meat. If the calories of [first_course] are light, then the calories of [second_course] should be heavy, and vice versa if the calories of [first_course] are heavy, the calories of [second_course]
should be light. [first_course] must be part of the Asian cuisine. [second_course] must be part of the Italian cuisine. If [first_course] is steamed, then [second_course] must also be steamed."

Costumer benefit

Answers more consistent with questions, increasing trust

Correct:
"Vegetable dumplings (steamed)"

"Steamed Cheese and Spinach Ravioli"

[Claude 3 Sonnet]

Three problems:
1. Use a critic aligned with truth of language $\Rightarrow$ LLM
2. How to combine the constraints
3. How to sample.

How to implement the theory solver of language?

"[entree] and [side] are vegetarian"

...

"[side] is heavy"

$ \left\{ \begin{aligned} L[c_1(x_1, \ldots, x_n)] \\ \,\\ L[c_m(x_1, \ldots, x_n)] \end{aligned} \right.$

...

The sum of the prices for 7 people of [transportation_1][breakfast_1], [lunch_1], [dinner_1], [accommodation_1], ... , [accommodation_3] does not exceed 30,200.

[accommodation_1], [accommodation_2], [accommodation_3] must be suited for 7 people.

Travel Plan:

Day 1:
[Current City_1]: from Ithaca to Charlotte
[Transportation_1]: Flight Number: F3633413...
[Breakfast_1]: Nagaland's Kitchen, Charlotte

....

LLM Replies (+ Self-refining procedure)

Results

Metrics: pass rate over satisfying commonsense and hard constraints with correct format (%)

Baselines: CoT, React

Results: from 3% to 7%, same as React with less LLM calls

PhD in AI: explaining the success of ML

Machine learning is highly effective across various tasks
Scaling laws: More training data leads to better performance

Curse of dimensionality occurs when learning structureless data in high dimension $d$:

Slow decay: $\beta=1/d$
Number of training data to learn is exponential in $d$.

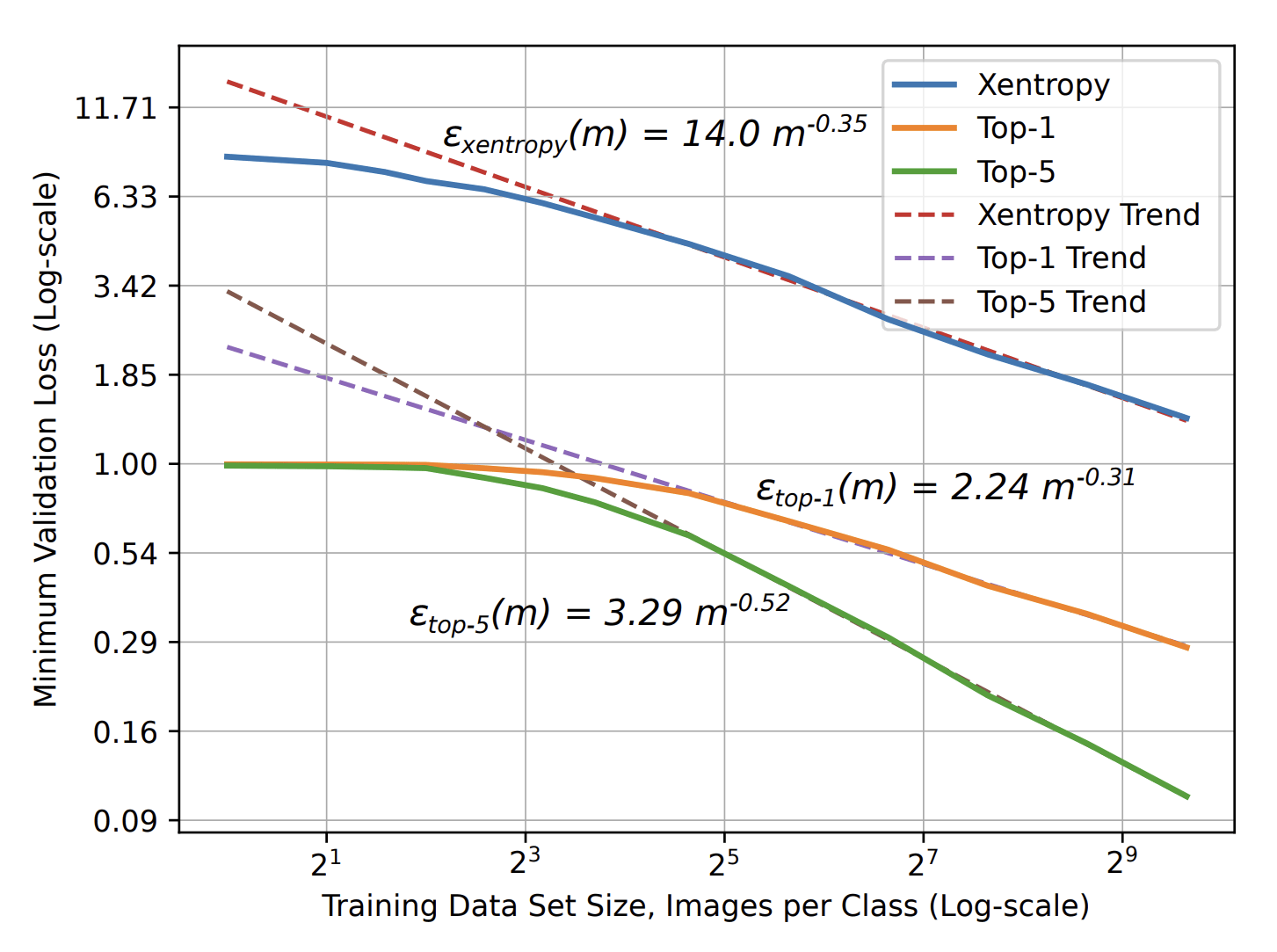
Image Classification: $\beta=\,0.3\,-\,0.5$
Speech Recognition: $\beta\approx\,0.3$
Language Modeling: $\beta\approx\,0.1$

$\varepsilon\sim P^{-\beta}$

$\Rightarrow$ Data must be structured and

Machine Learning should capture such structure.

Key questions motivating this thesis:

What constitutes a learnable structure?
How does Machine Learning exploit it?
How many training points are required?

Data must be Structured

Reducing complexity with depth

Deep networks build increasingly abstract representations with depth (also in brain)

How many training points are needed?
Why are these representations effective?

Intuition: reduces complexity of the task, ultimately beating curse of dimensionality.

Which irrelevant information is lost ?

Two ways for losing information

by learning invariances

Discrete

Continuous

[Zeiler and Fergus 14, Yosinski 15, Olah 17, Doimo 20,

Van Essen 83, Grill-Spector 04]

[Shwartz-Ziv and Tishby 17, Ansuini 19, Recanatesi 19, ]

[Bruna and Mallat 13, Mallat 16, Petrini 21]

Hierarchical structure

Hierarchical representations simplify the task
Do deep hierarchical representations exploit the hierarchical structure of data?

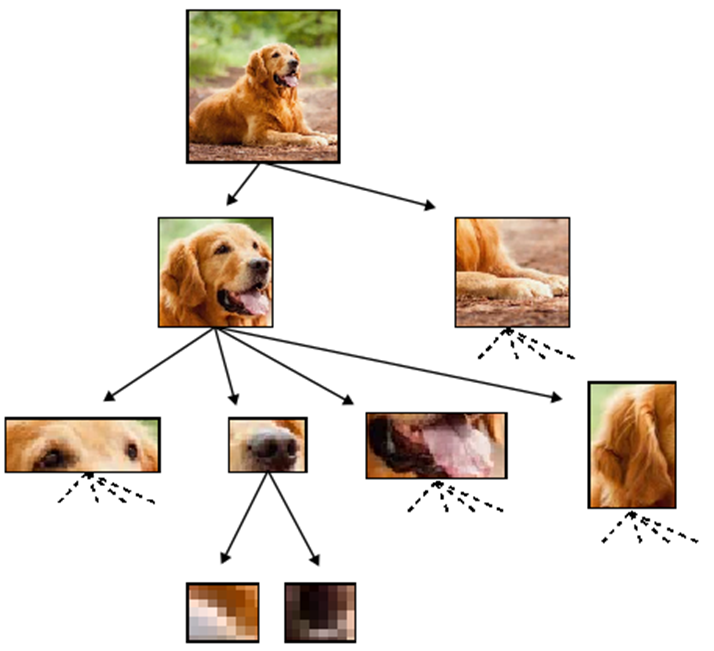
How many training points?

Quantitative predictions in a model of data

sofa

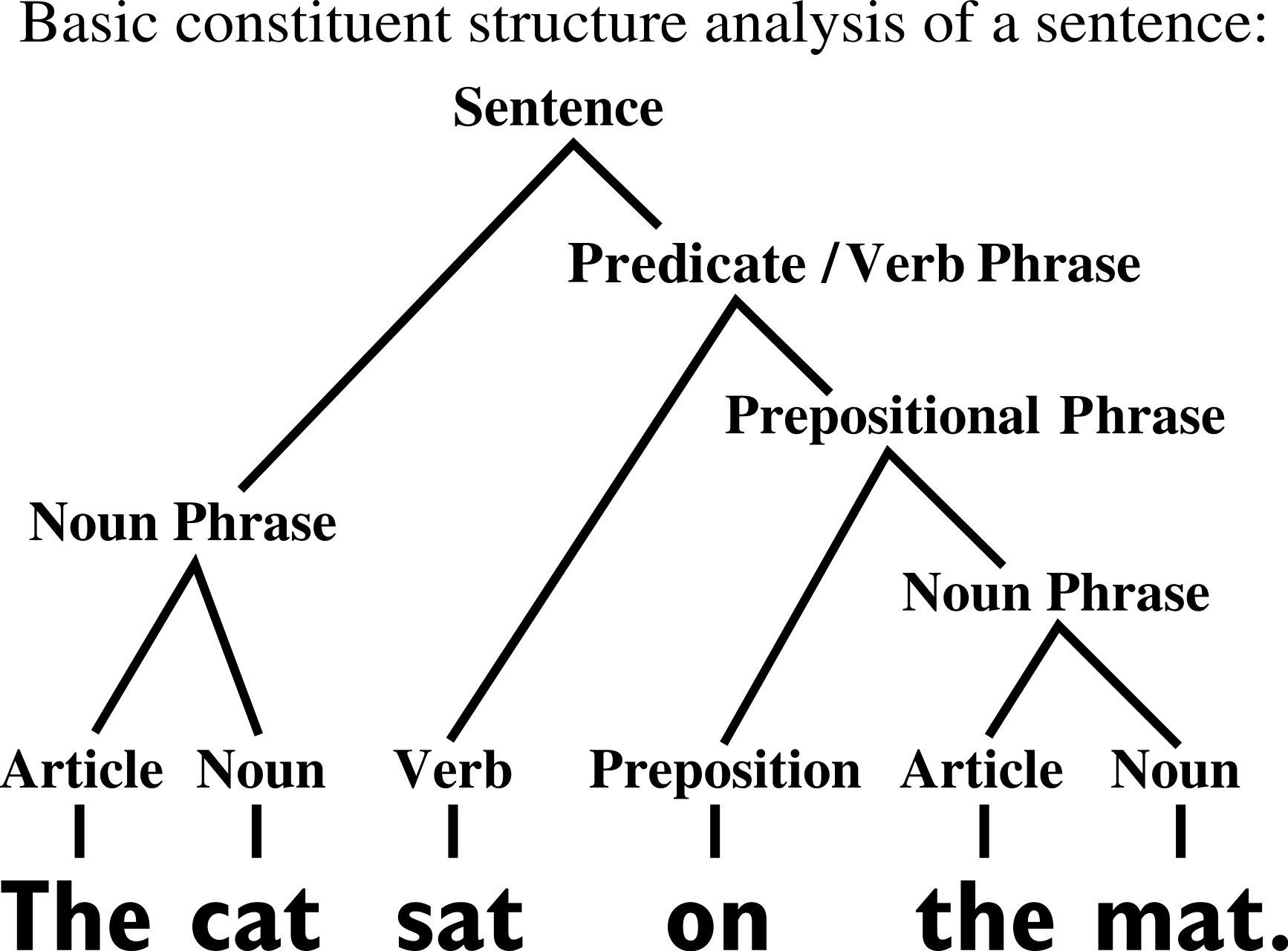
[Chomsky 1965]

[Grenander 1996]

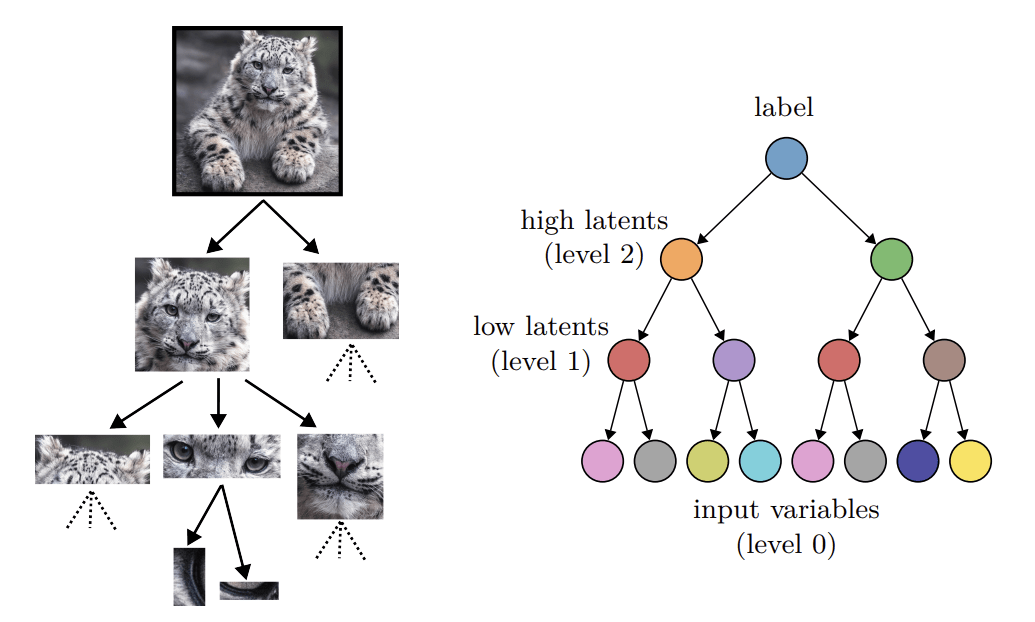
Random Hierarchy Model

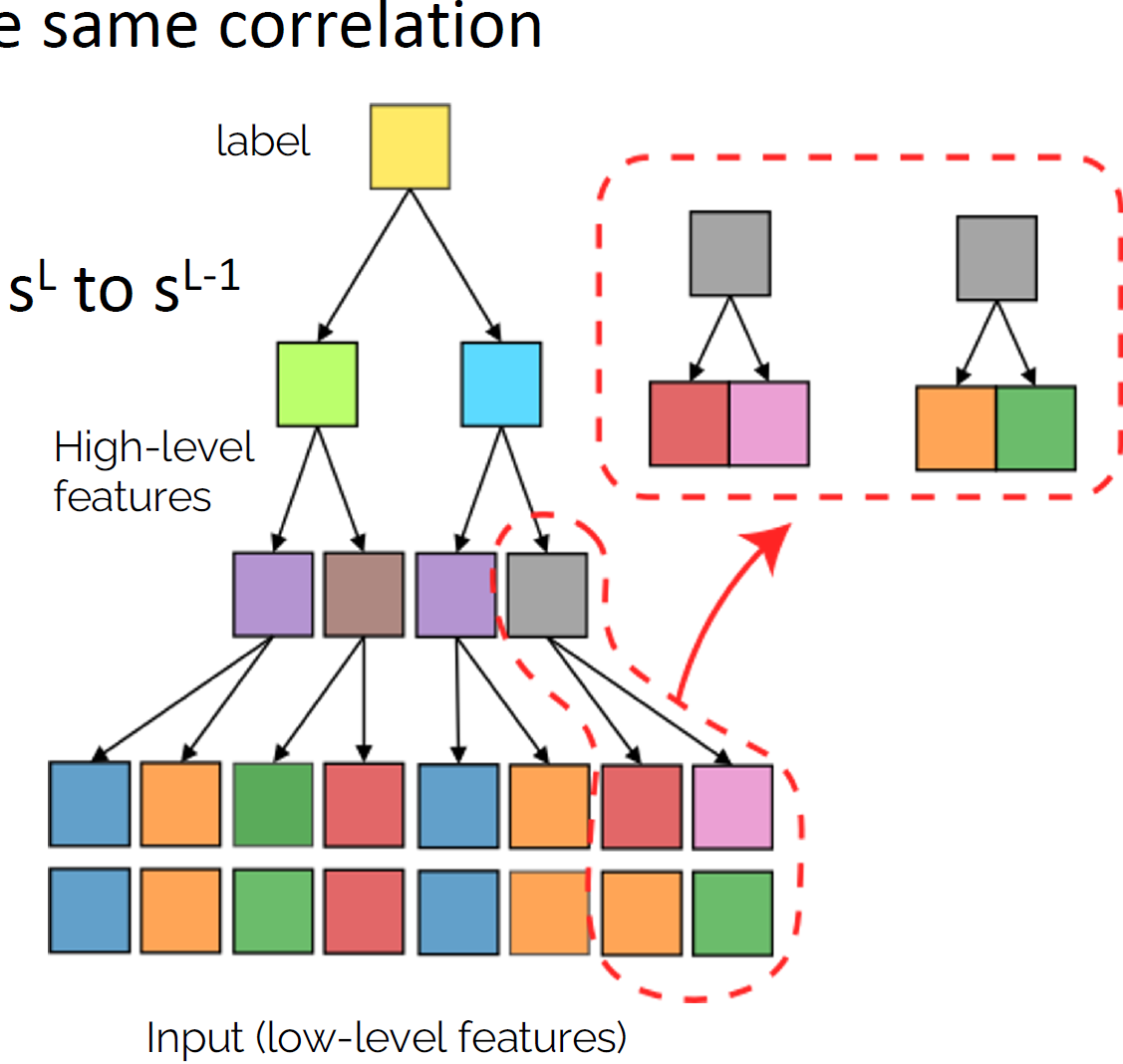
Classification task with $n_c$ classes
Generative model: label generates a patch of features
Patches chosen randomly from $m$ different random choices, called synonyms
Generation iterated $L$ times with a fixed tree topology.
Number of data: exponential in $d$, memorization not practical.

Deep networks learn with a number of data polynomial in the $d$

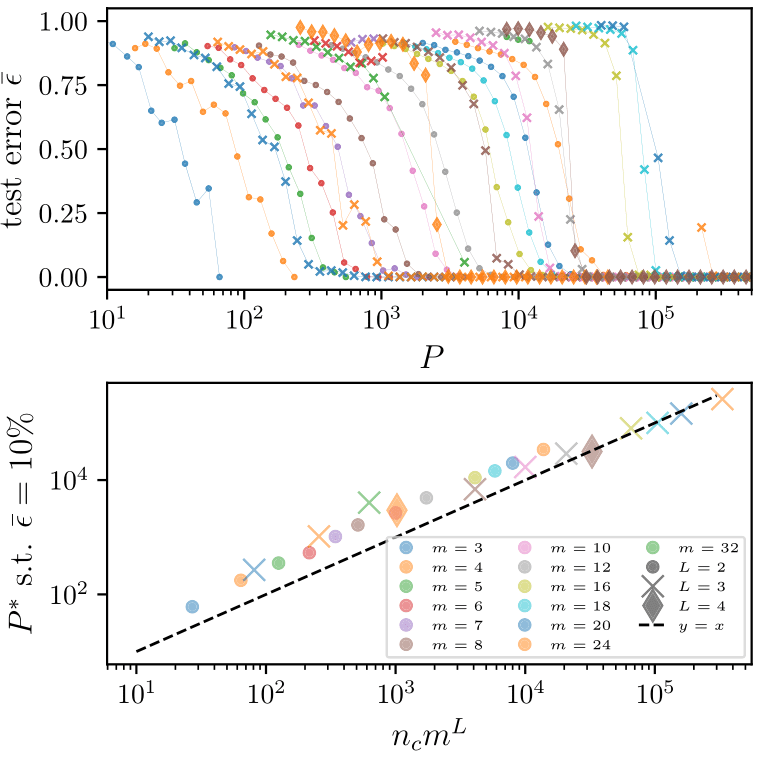
$P^*\sim n_c m^L$

How deep networks learn the hierarchy?

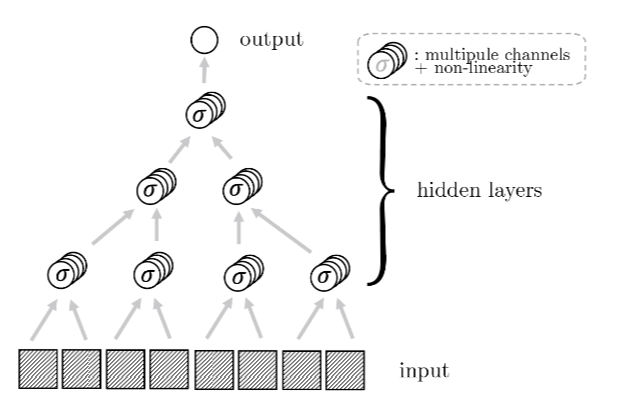
Intuition: build a hierarchical representation mirroring the hierarchical structure.
This representation is invariant to exchange of synonyms.

Takeaways

Deep networks learn hierarchical tasks with a number of data polynomial in the input dimension
They do so by developing internal representations that learn the hierarchical structure layer by layer

Application: generating novel data by probing hierarchical structure

Goal: generate new data from existing ones
At different levels of abstraction

Generative technique:

Diffusion models: add noise + denoise
Scale of change/features level depends on the noise amount
Prediction: intermediate level of noise at which this scale is maximal (phase transition)
Validated on images and text.
What about proteins?

Diffusion on protein sequences

Model for Discrete Diffusion: EvoDiff-MSA
Dataset: J-Domain proteins

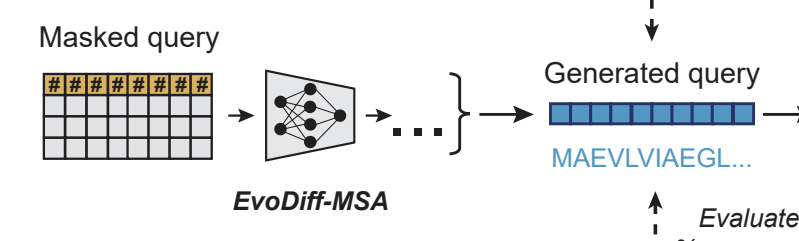
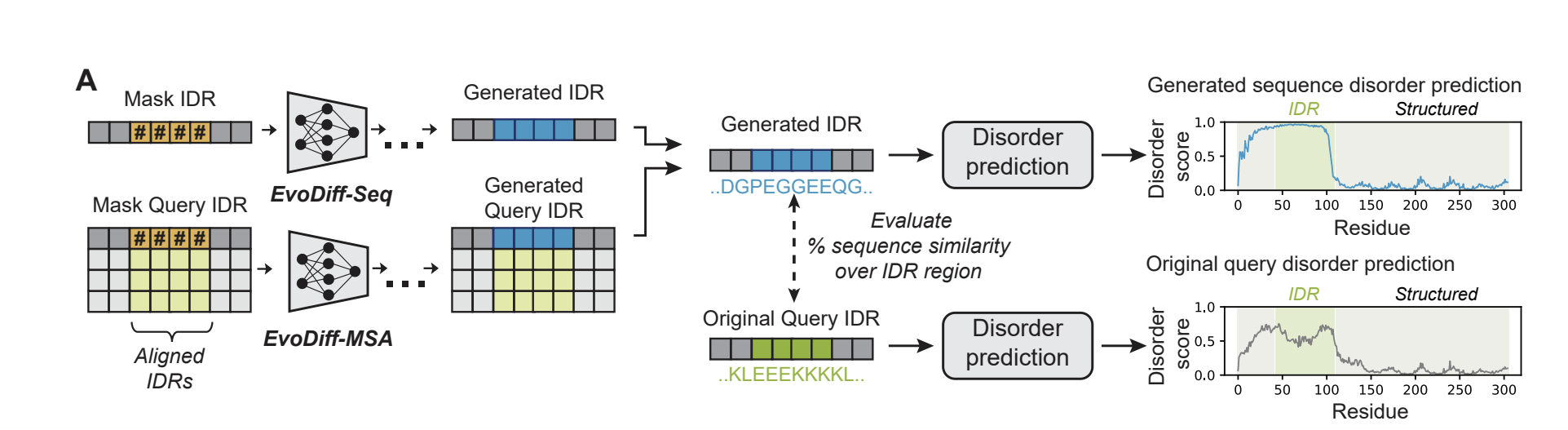
Note: Can be used to generate Intrinsically Disordered Regions (IDR) conditioning on structured regions