Education
- Bachelor in Physics (UniPD)
- Thesis on Quantum Mechanics
- Master in Physics of Matter (UniPD)
- Thesis on Statistical Physics and Climate models
- Supported by Excellence School scholarship

Work Experience
-
PhD in AI (EPFL):
- Quantify and interpret generalization in Deep Learning
- Research on Protein Design with Diffusion Models
- 5 papers (4 as first author) presented in 12 venues as ICLR and 2 ICML spotlights
-
Applied Scientist Intern (AWS AI Labs, California)
- Improve Large Language Models for complex reasoning
- One U.S. patent and 1 paper in preparation (first author).


PhD in AI: explaining the success of DL
- Machine learning is highly effective across various tasks
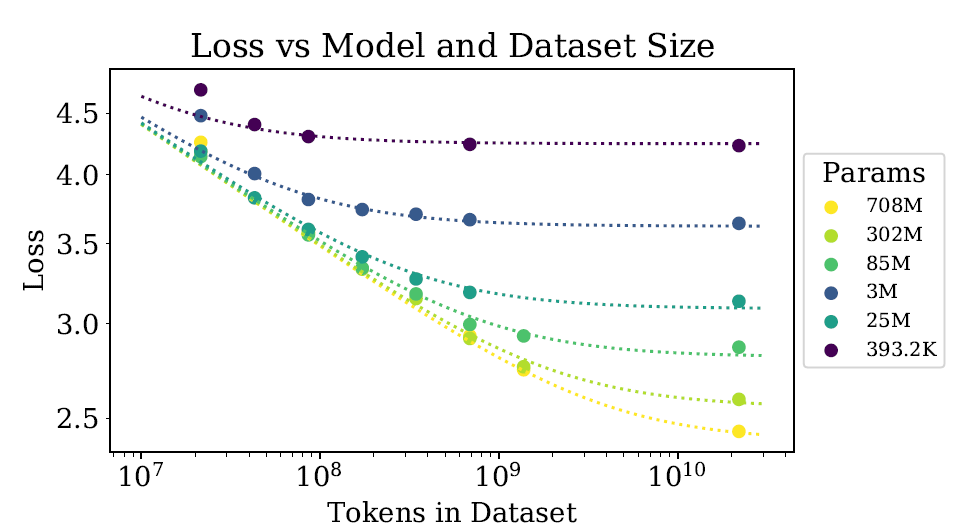
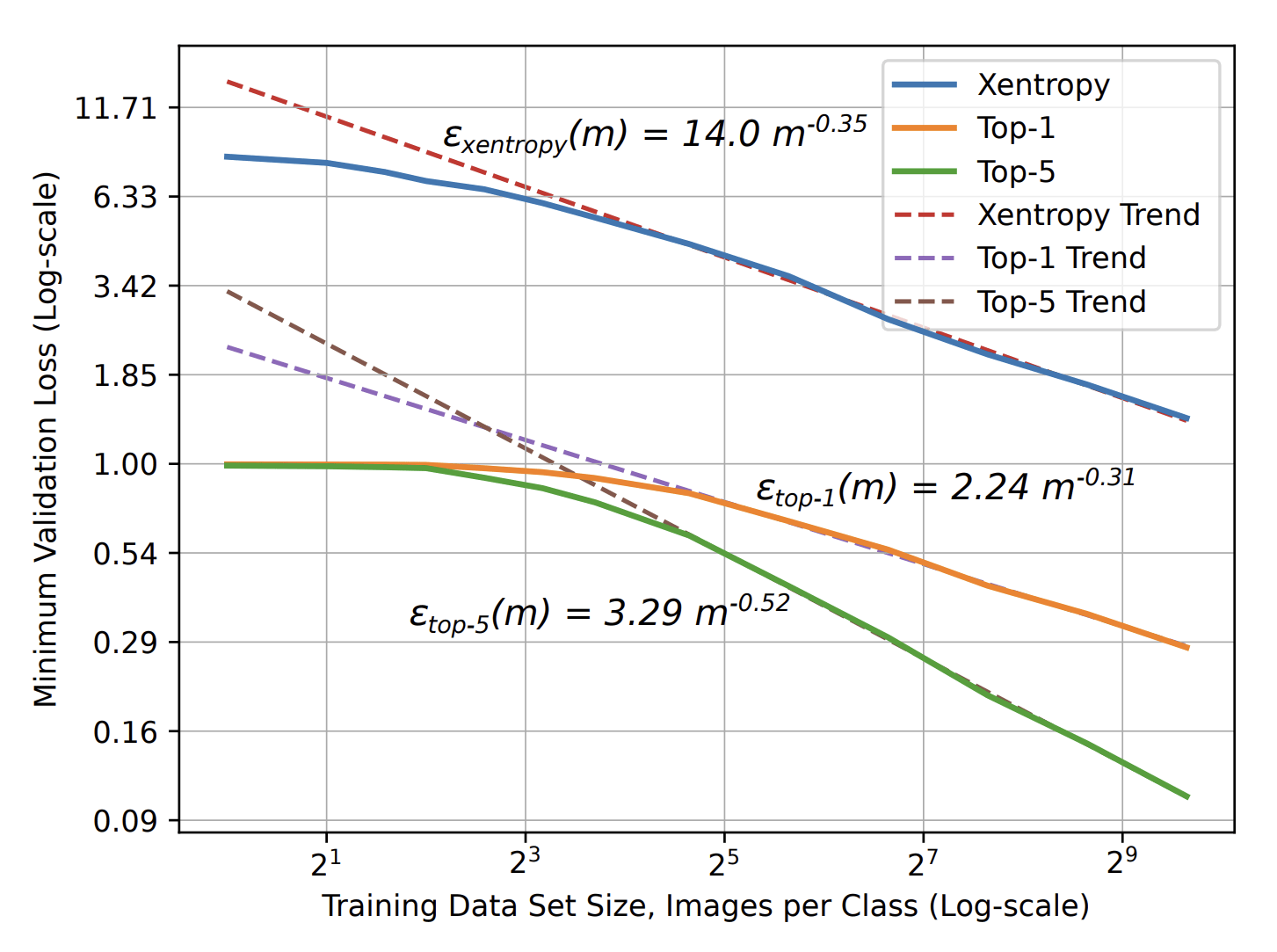
- Scaling laws: More training data leads to better performance
Curse of dimensionality occurs when learning structureless data in high dimension \(d\):
- Slow decay: \(\beta=1/d\)
- Number of training data to learn is exponential in \(d\).
- Language Modeling: \(\beta\approx\,0.1\)
- Image Classification: \(\beta=\,0.3\,-\,0.5\)
- Speech Recognition: \(\beta\approx\,0.3\)
VS
\(\varepsilon\sim P^{-\beta}\)
1/10
[Kaplan 20]
[Hestness 17]
\(\Rightarrow\) Data must be structured and
Machine Learning should capture such structure.
Key questions motivating this thesis:
- What constitutes a learnable structure?
- How does Machine Learning exploit it?
- How many training points are required?
Data must be Structured
2/10
Reducing complexity with depth

Deep networks build increasingly abstract representations with depth (also in brain)
- How many training points are needed?
- Why are these representations effective?
Intuition: reduces complexity of the task, ultimately beating curse of dimensionality.
- Which irrelevant information is lost ?

Two ways for losing information
by learning invariances


Discrete
Continuous
[Zeiler and Fergus 14, Yosinski 15, Olah 17, Doimo 20,
Van Essen 83, Grill-Spector 04]
[Shwartz-Ziv and Tishby 17, Ansuini 19, Recanatesi 19, ]
[Bruna and Mallat 13, Mallat 16, Petrini 21]
3/10
Hierarchical structure
- Hierarchical representations simplify the task
- Do deep hierarchical representations exploit the hierarchical structure of data?
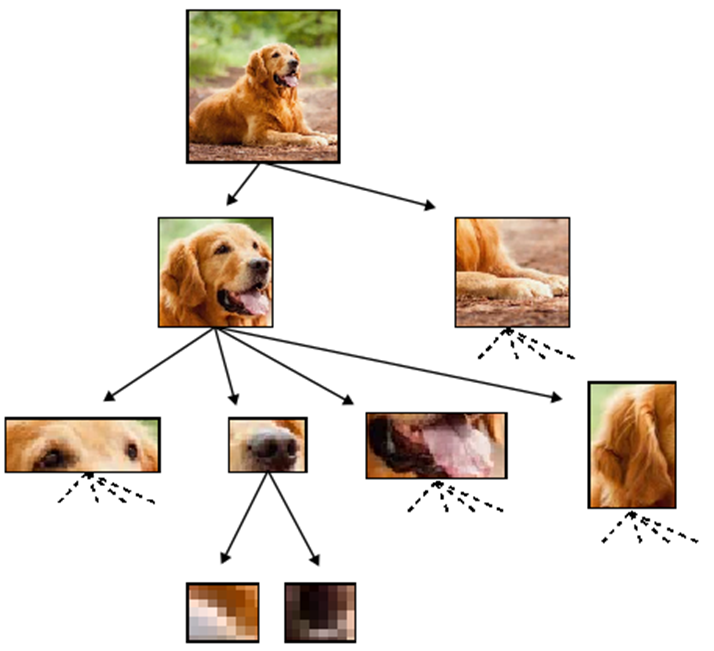
How many training points?
Quantitative predictions in a model of data
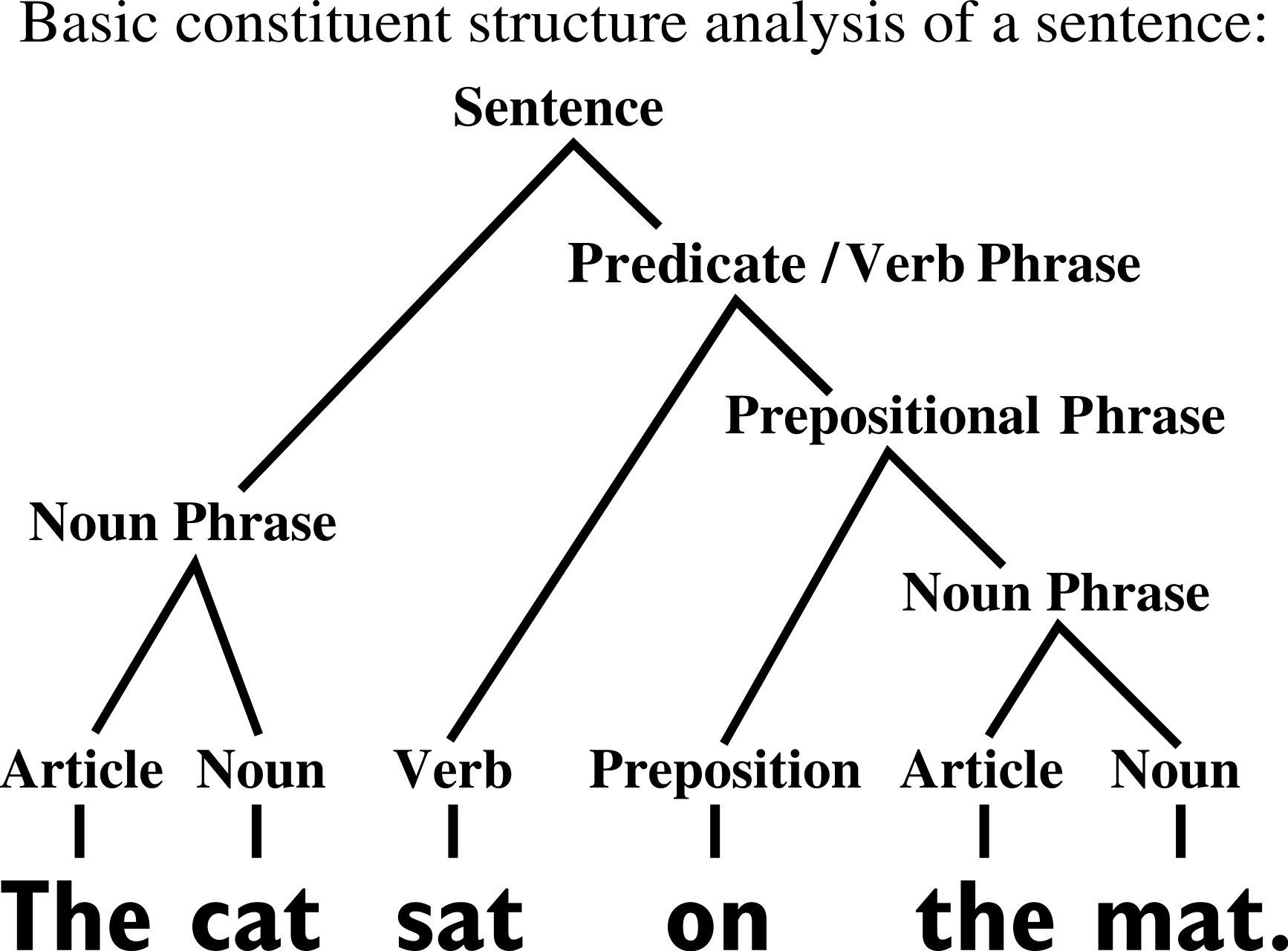
sofa
[Chomsky 1965]
[Grenander 1996]
4/10
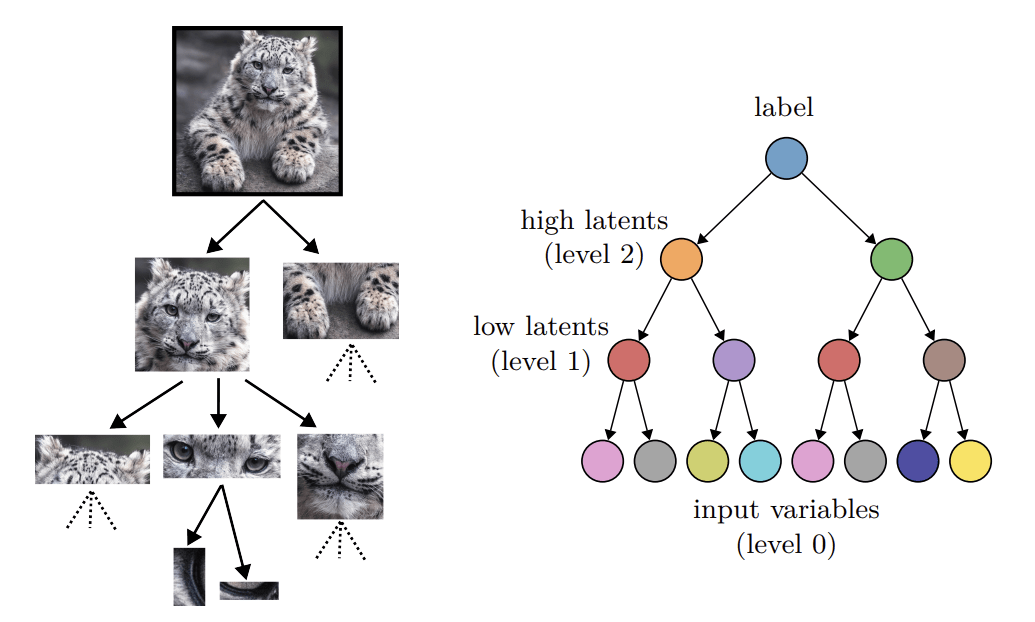
Random Hierarchy Model
- Classification task with \(n_c\) classes
-
Generative model of data:
- Label generates a patch of \(s\) features
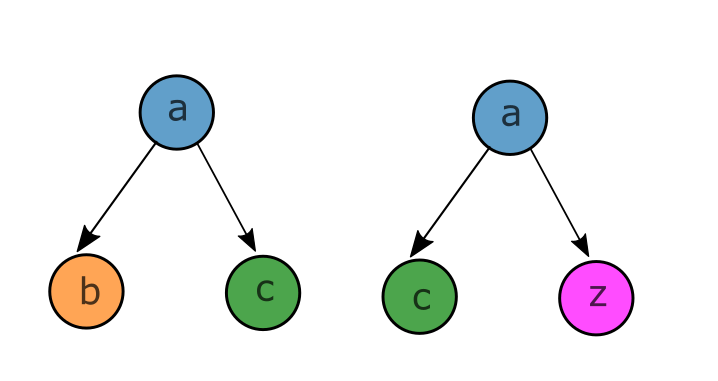
- Patches chosen randomly from \(m\) unambiguous choices (synonyms) according to random production rules,
- e.g. \(a\rightarrow (b,c) ; a\rightarrow (c,z)\)
- Generation iterated \(L\) times with a fixed tree topology.
- Number of data \(\sim e^{d}\), memorization not practical.

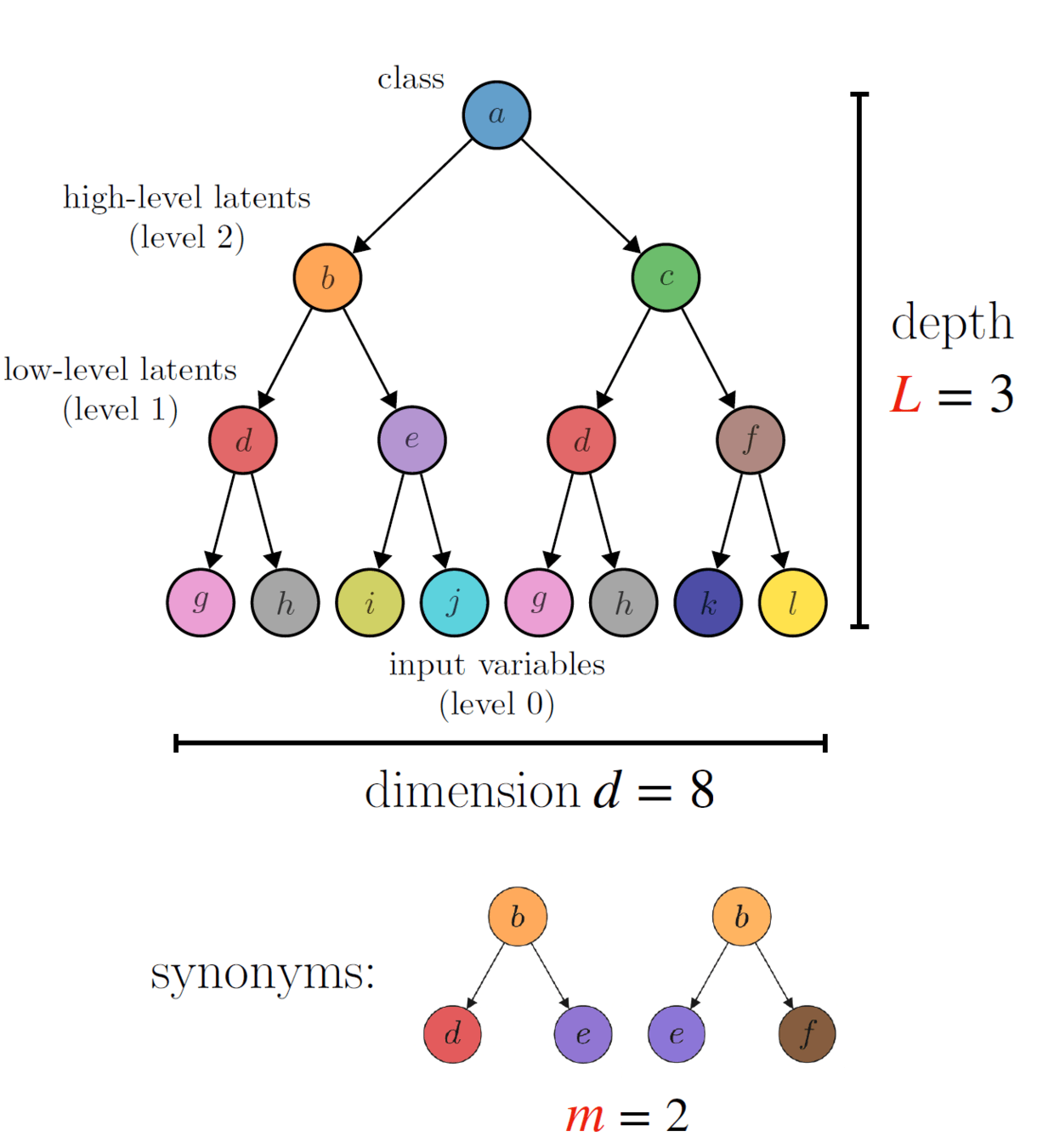
5/10
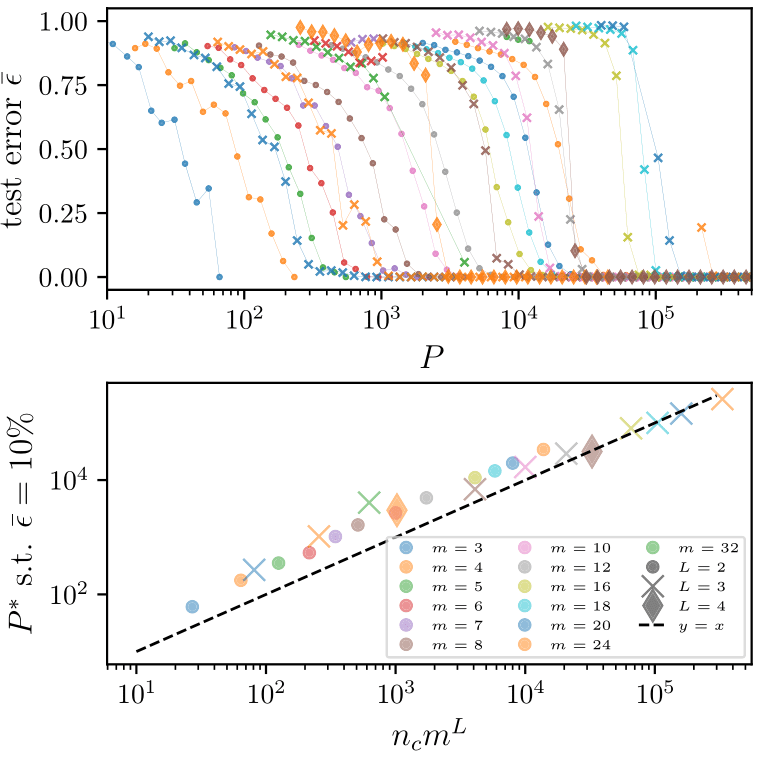
Deep networks beat the curse of dimensionality
\(P^*\)
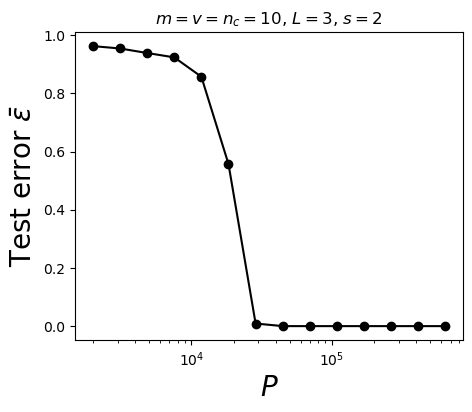
\(P^*\sim n_c m^L\)
- Polynomial in the input dimension \(s^L\)
- Beating the curse
- Shallow network \(\rightarrow\) cursed by dimensionality
- Depth is key to beat the curse
6/10
How deep networks learn the hierarchy?
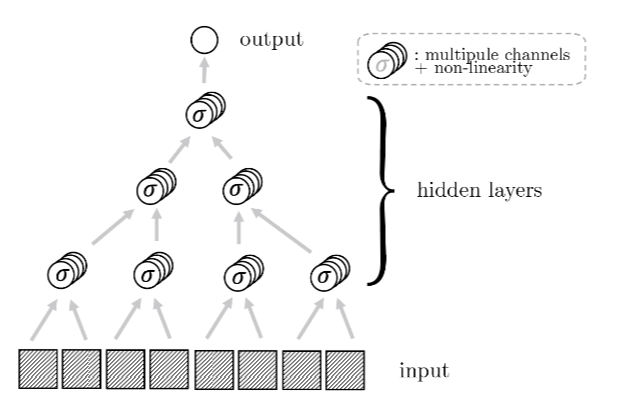
- Intuition: build a hierarchical representation mirroring the hierarchical structure. How to build such representation?
- Start from the bottom. Group synonyms: learn that patches in input correspond to the same higher-level feature
- Collapse representations for synonyms, lowering dimension from \(s^L\) to \(s^{L-1}\)
- Iterate \(L\) times to get hierarchy
How many training points are needed to group synonyms?
7/10

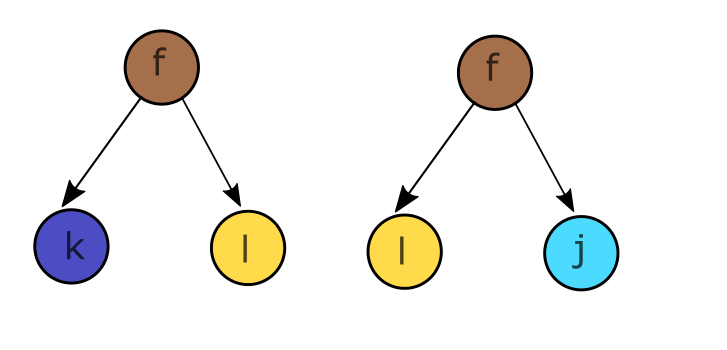
Grouping synonyms by correlations
- Synonyms are patches with same correlation with the label
- Measure correlations by counting
- Large enough training set is required to overcome sampling noise:
- \(P^*\sim n_c m^L\), same as sample complexity
- Simple argument: for \(P>P^*\) one step of Gradient Descent uses the synonyms-label correlations to collapse representations of synonyms
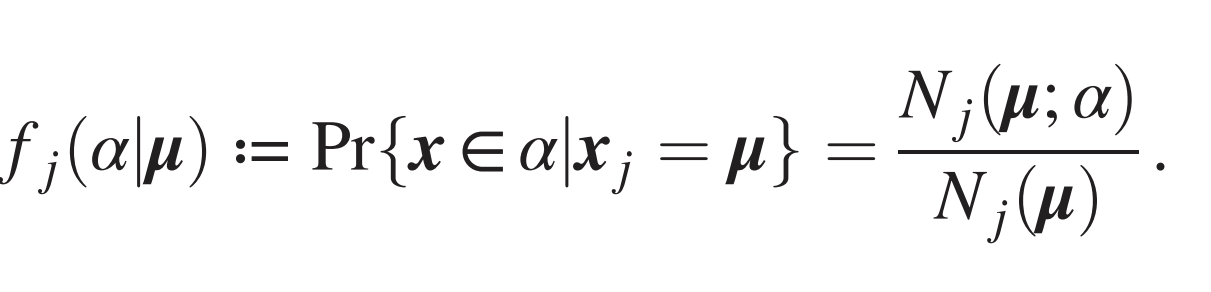
Patch \(\mu\)
Label \(\alpha\)
8/10


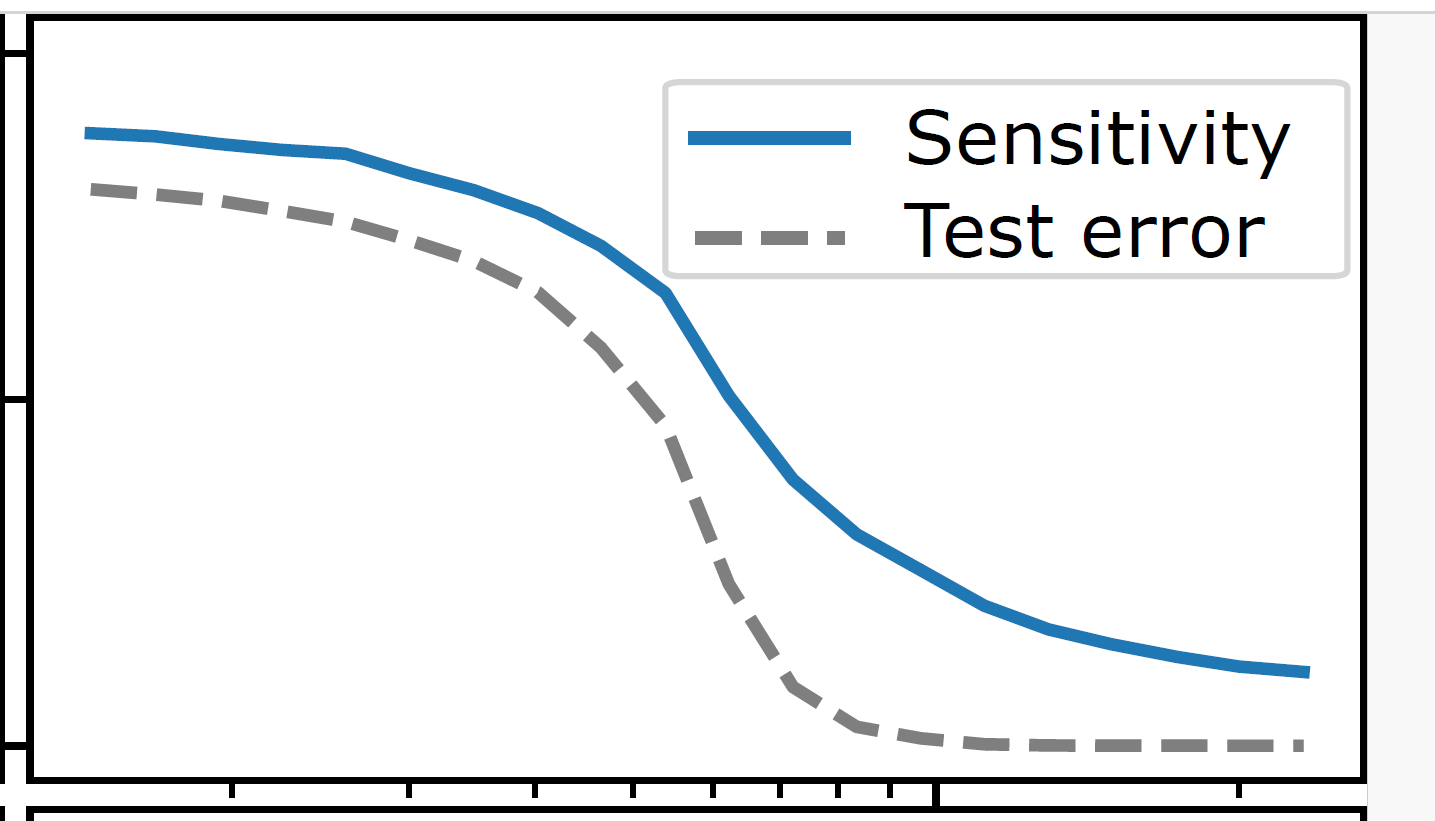
Testing whether deep representations collapse for synonyms
At \(P^*\) the task and the synonyms are learnt
- How much changing synonyms at first level in data change second layer representation (sensitivity)
- For \(P>P^*\) drops
1.0
0.5
0.0
\(10^4\)
Training set size \(P\)
9/10
Takeaways
- Deep networks learn hierarchical tasks with a number of data polynomial in the input dimension
- They do so by developing internal representations that learn the hierarchical structure layer by layer
Future directions
Thank you!
- Extend the RHM to more realistic models of data (e.g. no fixed topology), and interpret how LLMs/Visual Models learn them.
- Probe the hierarchical structure to generate data at different levels of abstraction (Diffusion Models).


sofa
28/28
Thank you!
10/10
Application: generating novel data by probing hierarchical structure

- Goal: generate new data from existing ones
- At different levels of abstraction
Generative technique:
- Diffusion models: add noise + denoise
- Scale of change/features level depends on the noise amount
- Prediction: intermediate level of noise at which this scale is maximal (phase transition)
- Validated on images and text.
- What about proteins?
Diffusion on protein sequences
- Model for Discrete Diffusion: EvoDiff-MSA
- Dataset: J-Domain proteins
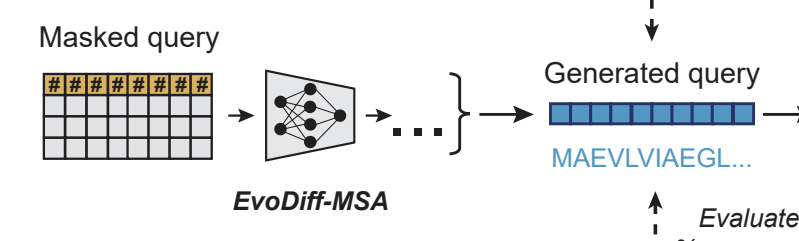
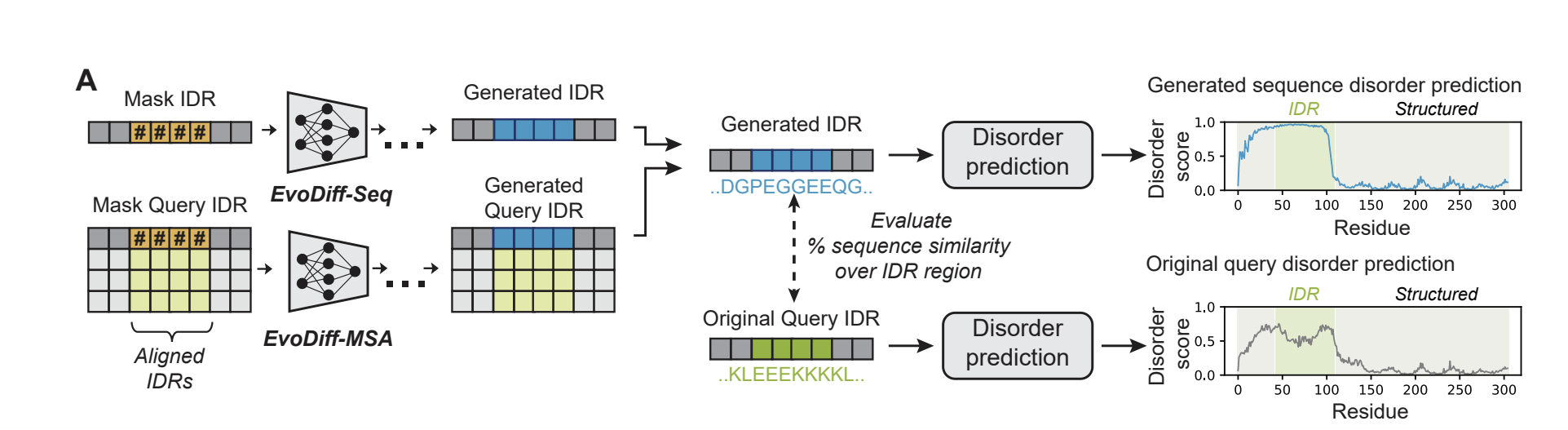
- Note: Can be used to generate Intrinsically Disordered Regions (IDR) conditioning on structured regions
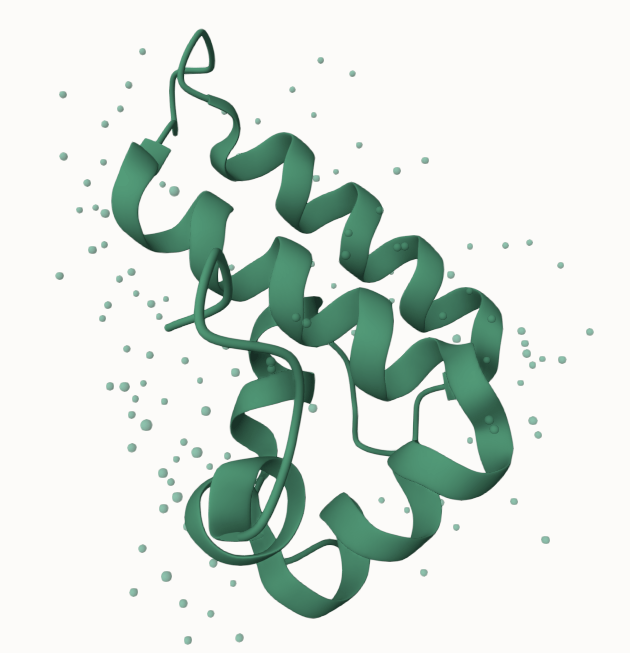
- Generate new sequences by adding noise to protein sequence+denoising
- Do not find a phase transition in the amount of change wrt noise
- Uniform change along whole sequence
- Not consistent with hierarchical structure
-
Future investigations:
- Better model
- Structure 3D space

Are protein sequences hierarchical?

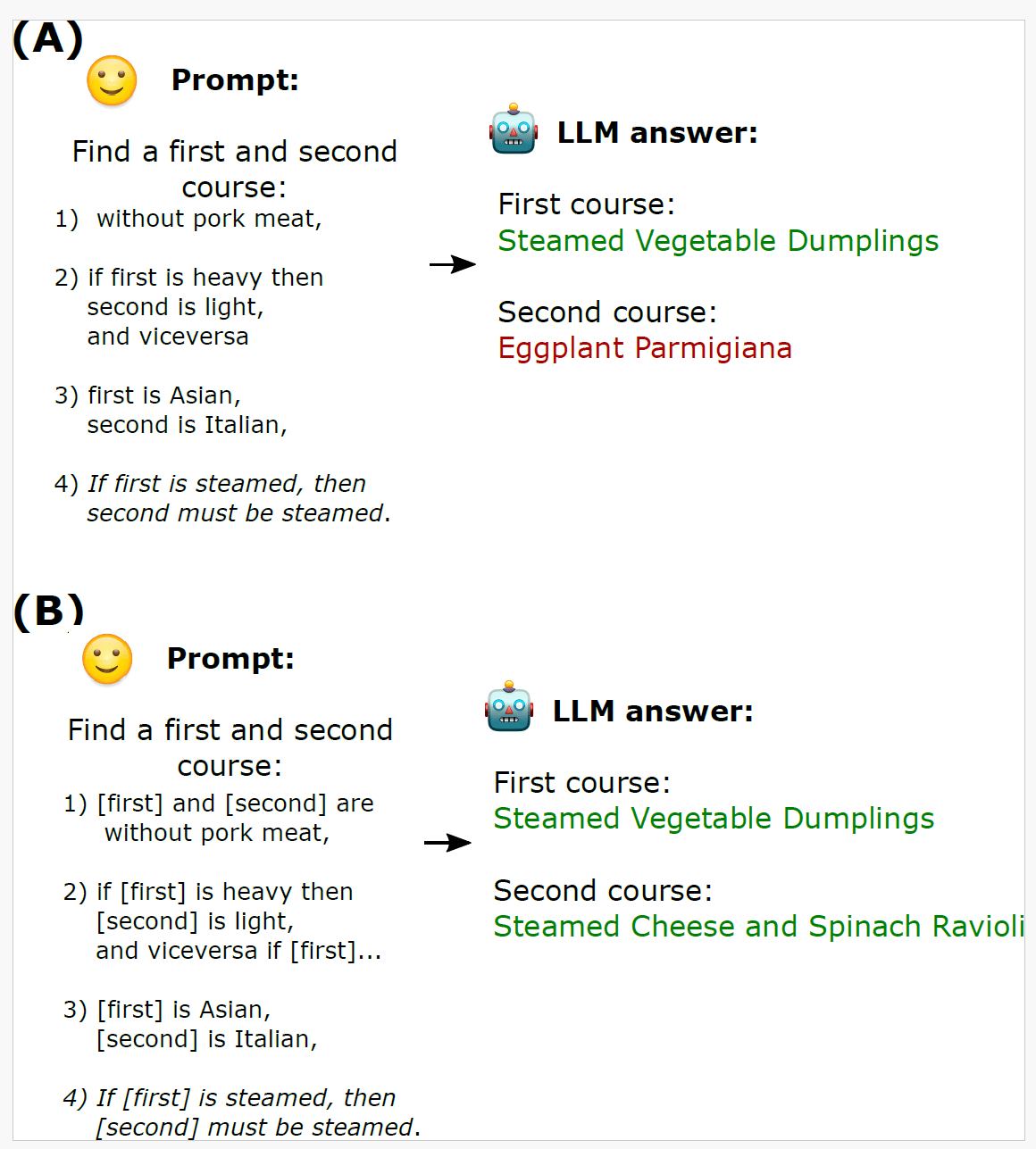
Natural Language Constraint Satisfiability Problems
The problem (NL-CSP):
- Finding a set of \(n\) objects which satisfy \(m\) constraints in the prompt
- Some commonsense, other hard constraints
- Crucial reasoning step in planning, common user interactions as querying databases...
Our approach:
- Formalize NL-CSPs as infilling problems
- Use a combination of formal solvers and LLMs to solve it
[U.S patent]

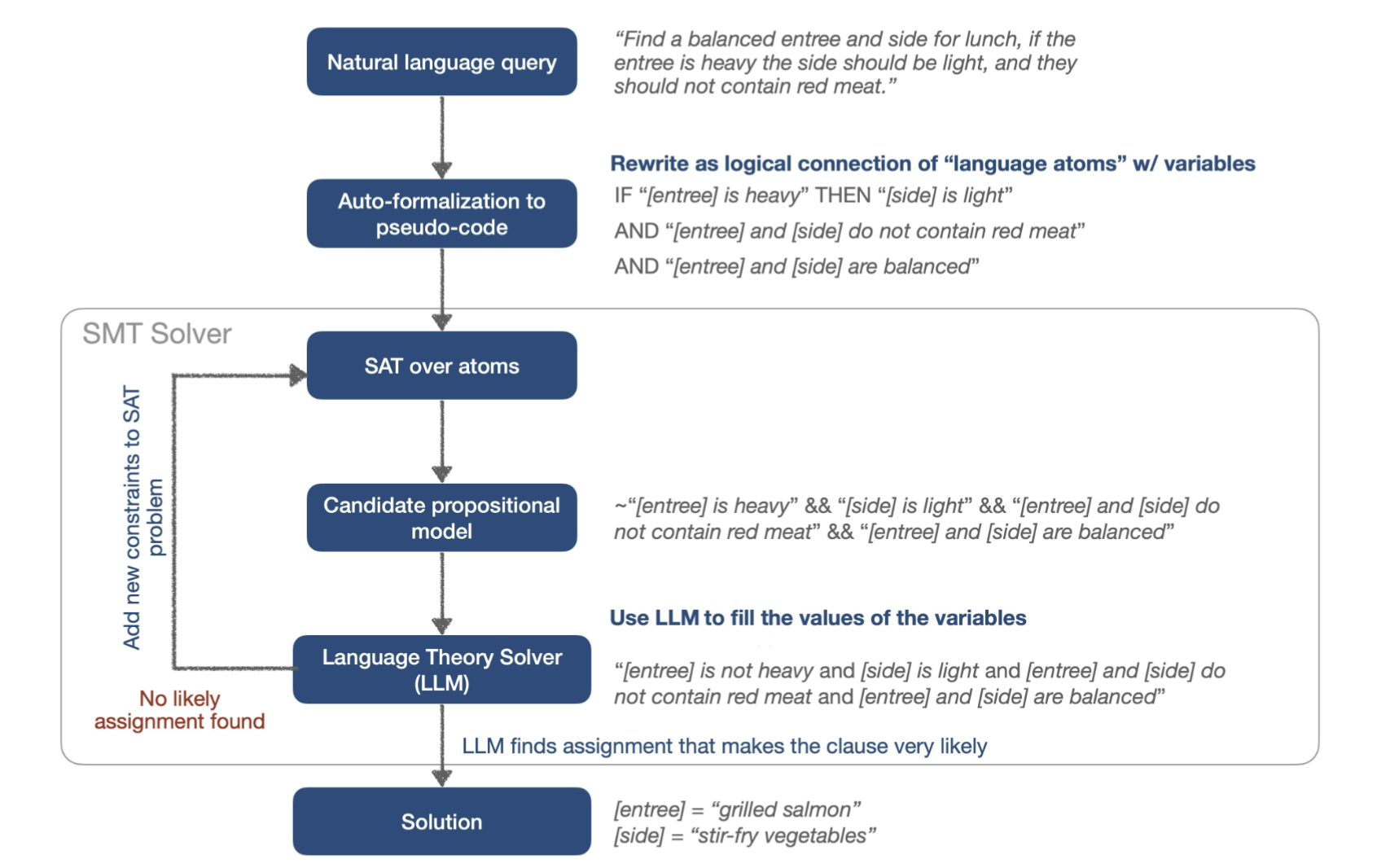
LLMs a Theory Solvers
Focus on LLM part:
- Open-weight models: improve accuracy at inference time by reweighting the logits (10-20%)
- Close-weight models: new prompting technique (2.5x improvement)
Umberto Tomasini - Mistral III
By umberto_tomasini
Umberto Tomasini - Mistral III
- 0


