Education
- Bachelor in Physics (UniPD)
- Thesis on Quantum Mechanics
- Master in Physics of Matter (UniPD)
- Thesis on Statistical Physics and Climate models
- Supported by Excellence School scholarship

Work Experience
-
PhD in AI (EPFL):
- Quantify and interpret generalization in Deep Learning
- Research on Protein Design with Diffusion Models
- 5 papers (4 as first author) presented in 12 venues as ICLR and 2 ICML spotlights
-
Applied Scientist Intern (AWS AI Labs, California)
- Improve Large Language Models for complex reasoning
- One U.S. patent and 1 paper in preparation (first author).



[U.S patent]
Language Models as Theory Solvers

Amazon Shopping with Rufus
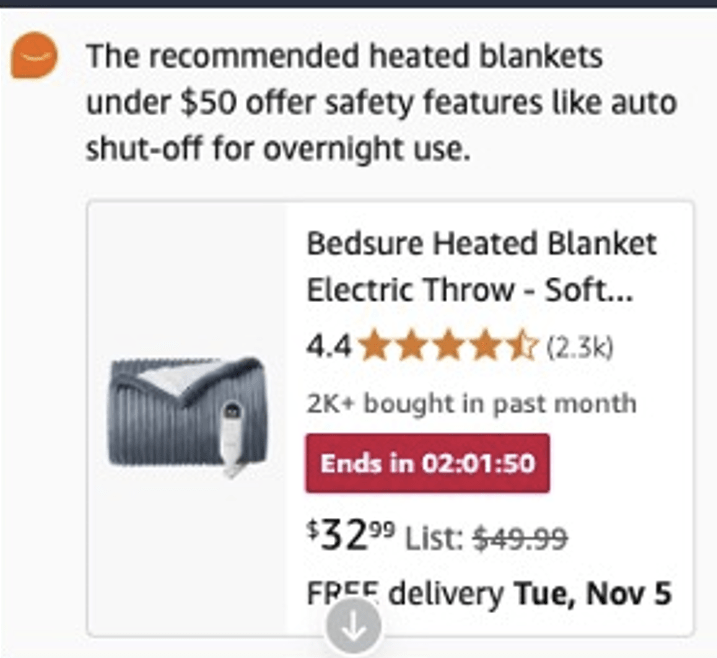

Working Backwords
Wrong! More than $30, polyester.
Much general problem...
- Planning
- Calendaring
- Storytelling
- ...
Every time you need an answer with many constraints
Goal: enable LLMs to generate correct answers,
even with many constraints
SAT or SMT solvers solve statements with many constraints.
For example an SMT would find \(x\), \(y\), \(z\) to solve:
\(x*z=y\land(z<0\lor y=0)\)
Used in applications as automated theorem proving and software testing (AWS team).
Many constraints: formal solvers
Query: "I want a pet. Hyena or cat?"
Needs lot of additional information:
\(\Rightarrow\)needs an extensive ontology.
But also the point of the question is fuzzy, answering needs commonsense.
LLMs already have commonsense grounded in them.
SMT for language is not scalable
- Is a hyena legal to keep in the US?
- Is a hyena considered a pet?
- Is a hyena dangerous?
Method idea: merge LLMs with formal solvers
- LLMs: world knowledge for informal reasoning
- Formal solvers: logical consistency
\(x+y =3\)
IF \(x > 2\):
\(y = 0\)
1. SAT solver chooses which statements satisfy, e.g . :
\(x+y = 3\) AND \(x> 2\) AND \(y= 0\)
2. Theory solver:
\(x=3\), \(y = 0\)
SMT solvers first simplify, then solve
1. SAT solver chooses which constraints satisfy, e.g .:
[entree] and [side] are vegetarian. [entree] is heavy. [side] is light.
2. Theory solver:
[entree] is "Falafel".
[side] is "Salad".
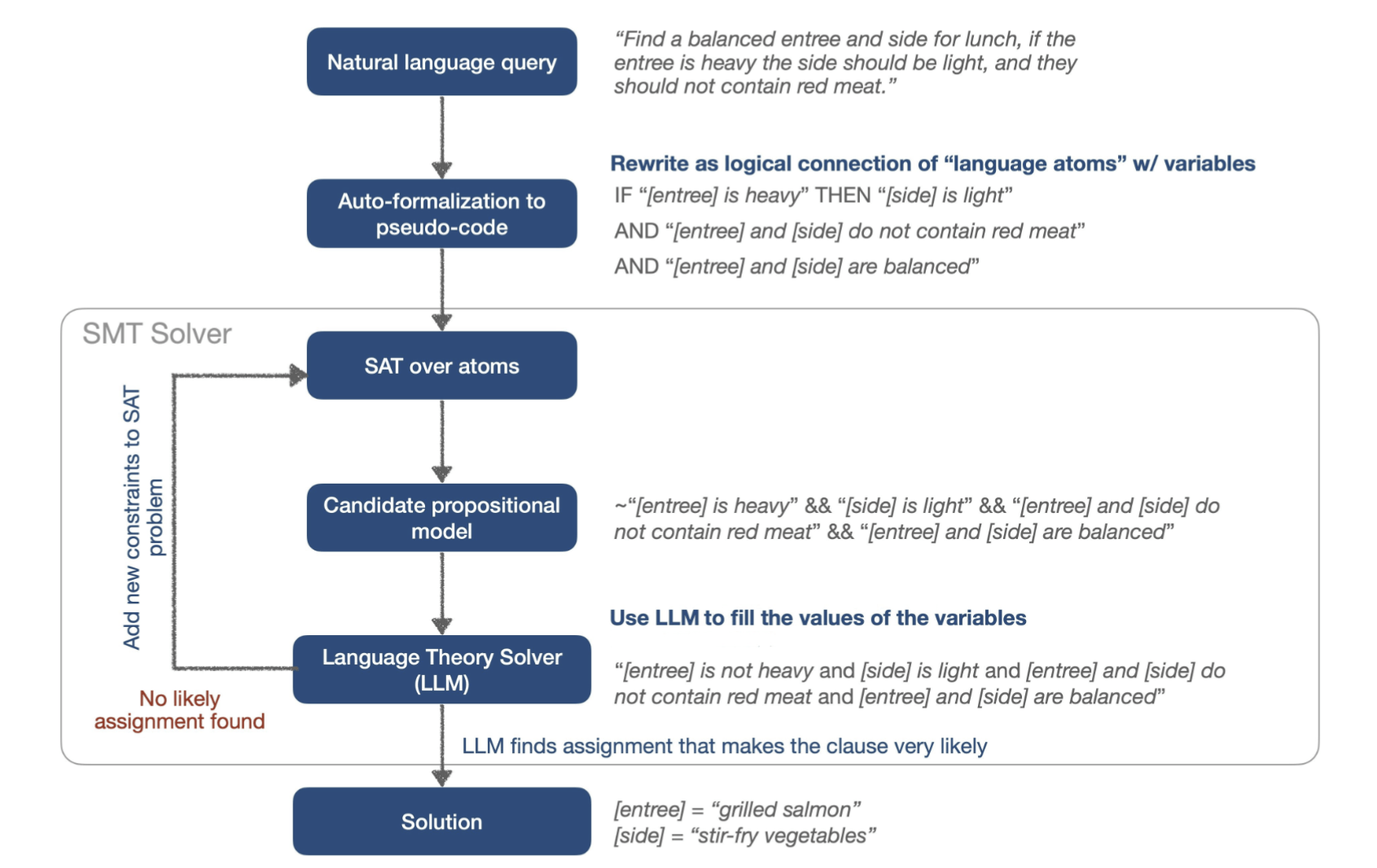
Language tasks
Find vegetarian entree and side.
If the entree is heavy then the side is light.
Query:
Constraint-explicit:
[entree] and [side] are vegetarian.
IF [entree] is heavy THEN [side] is light.
LLMs a Theory Solvers
"Find a first and second course without pork meat. The first course should be from Asian cuisine, and the second from Italian cuisine. If the first course is light in calories, the second should be heavy, and vice versa. If the first course is steamed, the second must also be steamed"
Failure:
"Vegetable dumplings (steamed)"
"Eggplant Parmigiana (baked)"
Costumer benefit
Answers more consistent with questions, increasing trust
[Claude 3 Sonnet]
"[first_course] and [second_course] are dishes without pork meat. If the calories of [first_course] are light, then the calories of [second_course] should be heavy, and vice versa if the calories of [first_course] are heavy, the calories of [second_course]
should be light. [first_course] must be part of the Asian cuisine. [second_course] must be part of the Italian cuisine. If [first_course] is steamed, then [second_course] must also be steamed."
Costumer benefit
Answers more consistent with questions, increasing trust
Correct:
"Vegetable dumplings (steamed)"
"Steamed Cheese and Spinach Ravioli"
[Claude 3 Sonnet]
Three problems:
1. Use a critic aligned with truth of language \(\Rightarrow\) LLM
2. How to combine the constraints
3. How to sample.
How to implement the theory solver of language?
"[entree] and [side] are vegetarian"
...
"[side] is heavy"
\( \left\{ \begin{aligned} L[c_1(x_1, \ldots, x_n)] \\ \,\\ L[c_m(x_1, \ldots, x_n)] \end{aligned} \right.\)
...
Open-weight models
Is LLM loss a good proxy of truth of language?
Aligning loss with accuracy
Prompt: \(T_{1, ... ,m} = T(c_1, ... , C_m)\)
Human: [x_1] and [x_2] are vegetarian [x_1] is high in calories.
Loss: \(-\log p(x_1,x_2|T_{1,...,m})\)
Answer: [x_1] is "rice".[x_2] is "salad".
Instead of:
Answer: [x_1] is "Falafel". [x_2] is "salad".
LLM not a good proxy for truth, dominated by the complexity of
syntax rather than semantics.
Removing Token Bias to increase reliability
- Proposed a new benchmark
- Finding a set of \(n\) objects which satisfy \(m\) constraints in the prompt
- Improved accuracy at inference time by reweighting the logits (10-20%)
Close-weight models
- Stronger models (e.g. Claude)
- No need for loss: just prompt the model!
Query example:
Could you create a travel plan for 7 people from Ithaca to Charlotte spanning 3 days, from March 8th to March 14th, 2022, with a budget of $30,200?
Challenging dataset!
\(\Rightarrow\) 2.8% for Claude 3.5-Sonnet and 4.4% for GPT-4-Turbo.
We can improve Claude of more than 200%!
From 3% to 7%
TravelPlanner: benchmark for real-world planning

Constraints (already annotated, can be scaled with LLM):
The sum of the prices for 7 people of [transportation_1][breakfast_1], [lunch_1], [dinner_1], [accommodation_1], ... , [accommodation_3] does not exceed 30,200.
[accommodation_1], [accommodation_2], [accommodation_3] must be suited for 7 people.
Planning as Constraint satisfiability
Query example:
Could you create a travel plan for 7 people from Ithaca to Charlotte spanning 3 days, from March 8th to March 14th, 2022, with a budget of $30,200?
The sum of the prices for 7 people of [transportation_1][breakfast_1], [lunch_1], [dinner_1], [accommodation_1], ... , [accommodation_3] does not exceed 30,200.
[accommodation_1], [accommodation_2], [accommodation_3] must be suited for 7 people.
Travel Plan:
Day 1:
[Current City_1]: from Ithaca to Charlotte
[Transportation_1]: Flight Number: F3633413...
[Breakfast_1]: Nagaland's Kitchen, Charlotte
....
LLM Replies
We propose a method to use LLMs as theory solvers for constrained language tasks, in tandem with formal solvers:
- A first approximation is zero-shot prompting (black-box models). In TravelPlanner, we go from 2.8% to 7.2%.
- For open-source models, we can manipulate the loss to improve consistency with constraints. Removing token bias, we improve 10-20% in relative terms on a toy dataset.
Conclusions
PhD in AI: explaining the success of ML
- Machine learning is highly effective across various tasks
- Scaling laws: More training data leads to better performance
Curse of dimensionality occurs when learning structureless data in high dimension \(d\):
- Slow decay: \(\beta=1/d\)
- Number of training data to learn is exponential in \(d\).
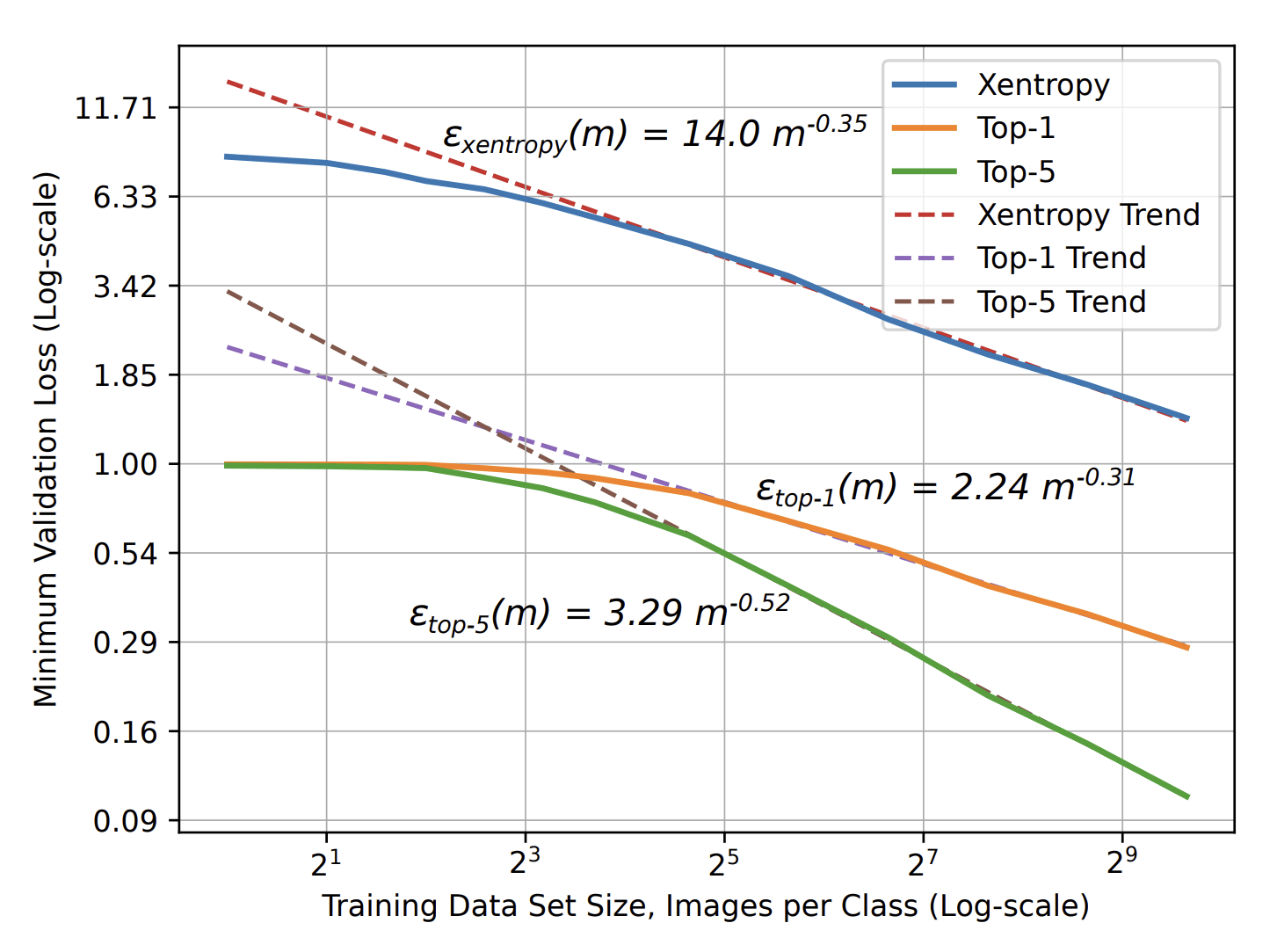
- Image Classification: \(\beta=\,0.3\,-\,0.5\)
- Speech Recognition: \(\beta\approx\,0.3\)
- Language Modeling: \(\beta\approx\,0.1\)
VS
\(\varepsilon\sim P^{-\beta}\)
\(\Rightarrow\) Data must be structured and
Machine Learning should capture such structure.
Key questions motivating this thesis:
- What constitutes a learnable structure?
- How does Machine Learning exploit it?
- How many training points are required?
Data must be Structured
Reducing complexity with depth

Deep networks build increasingly abstract representations with depth (also in brain)
- How many training points are needed?
- Why are these representations effective?
Intuition: reduces complexity of the task, ultimately beating curse of dimensionality.
- Which irrelevant information is lost ?

Two ways for losing information
by learning invariances


Discrete
Continuous
[Zeiler and Fergus 14, Yosinski 15, Olah 17, Doimo 20,
Van Essen 83, Grill-Spector 04]
[Shwartz-Ziv and Tishby 17, Ansuini 19, Recanatesi 19, ]
[Bruna and Mallat 13, Mallat 16, Petrini 21]
Hierarchical structure
- Hierarchical representations simplify the task
- Do deep hierarchical representations exploit the hierarchical structure of data?
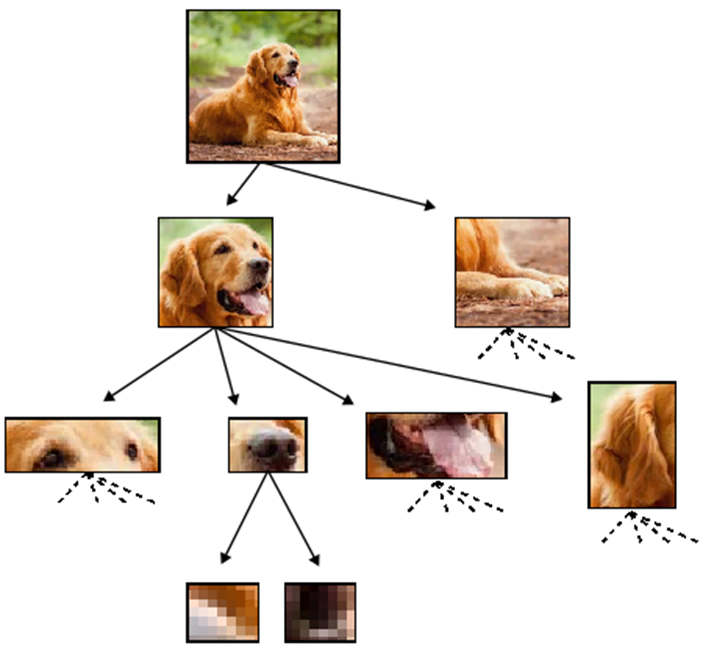
How many training points?
Quantitative predictions in a model of data
sofa
[Chomsky 1965]
[Grenander 1996]
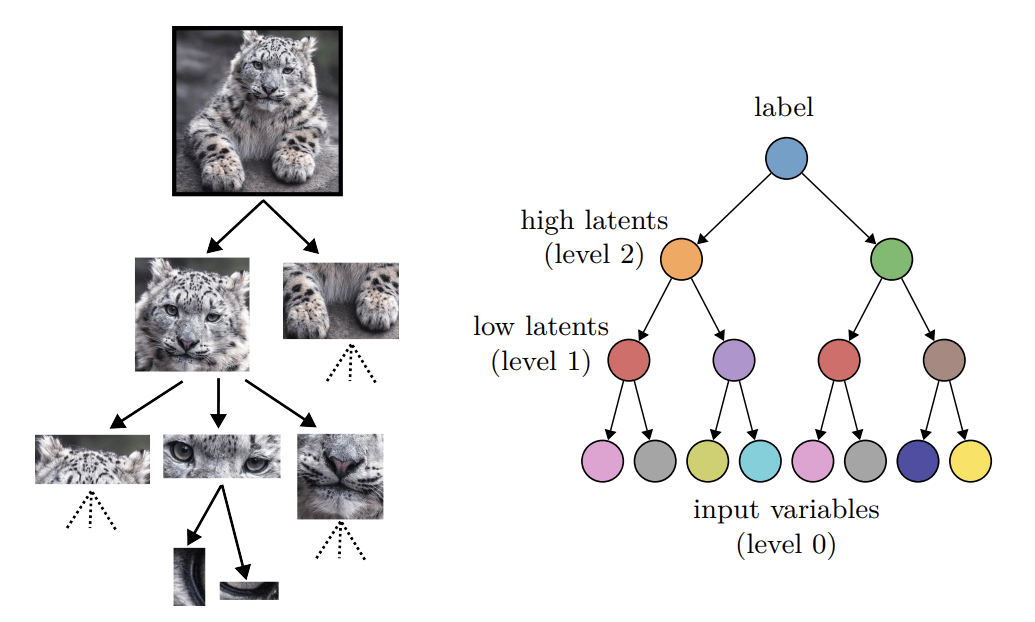
Random Hierarchy Model
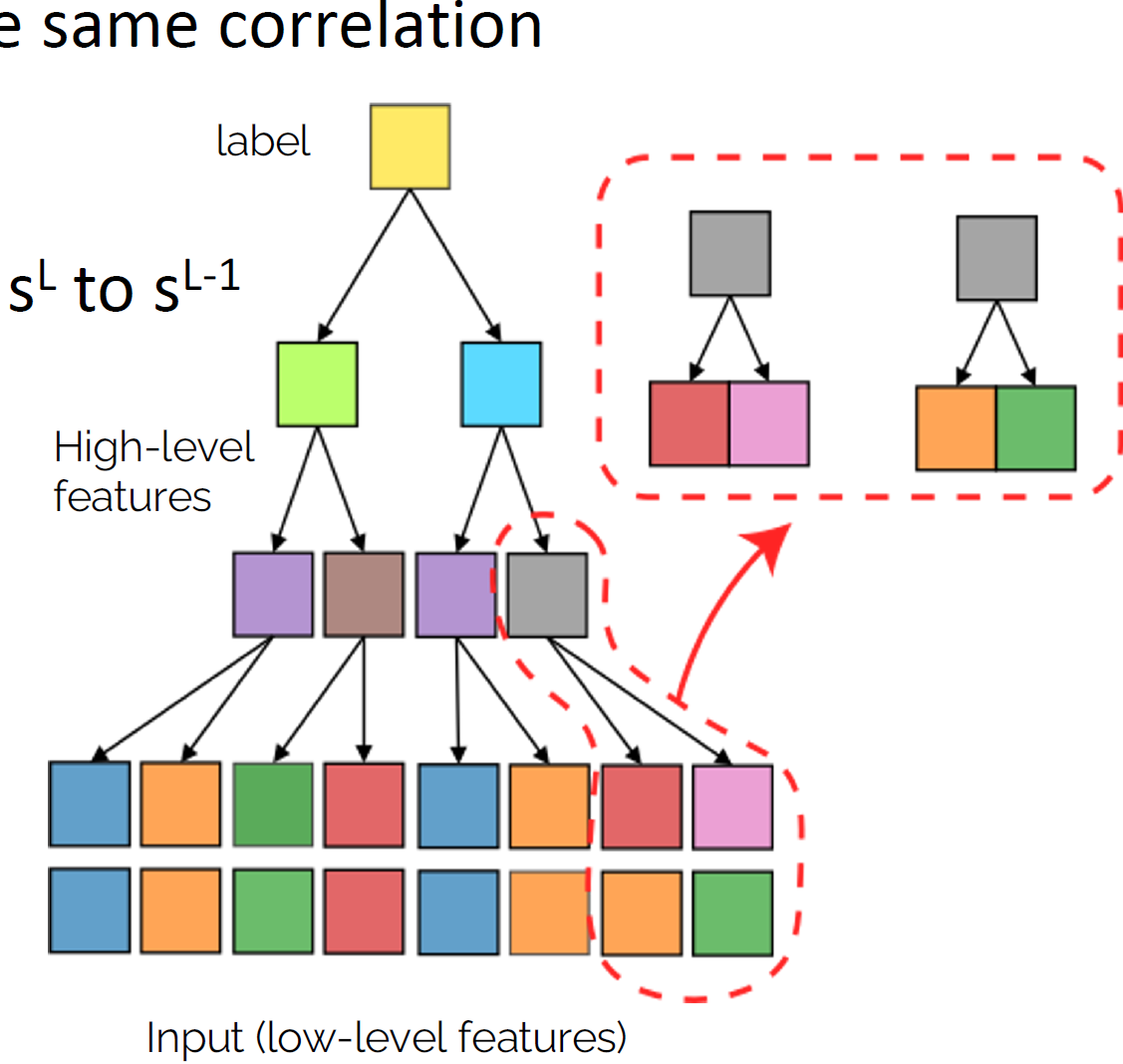
- Classification task with \(n_c\) classes
- Generative model: label generates a patch of features
- Patches chosen randomly from \(m\) different random choices, called synonyms
- Generation iterated \(L\) times with a fixed tree topology.
- Number of data: exponential in \(d\), memorization not practical.
Deep networks learn with a number of data polynomial in the \(d\)
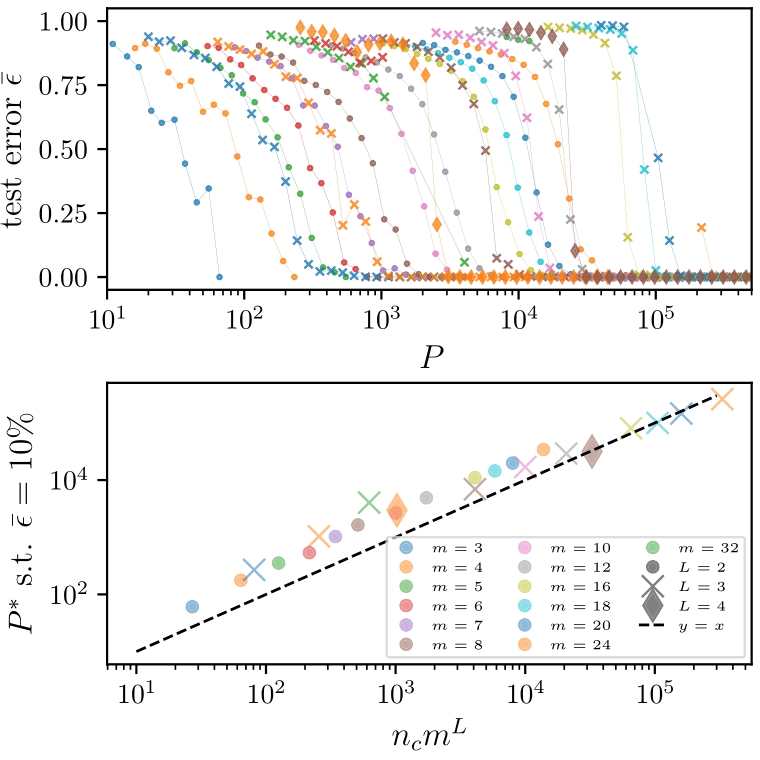
\(P^*\sim n_c m^L\)

How deep networks learn the hierarchy?

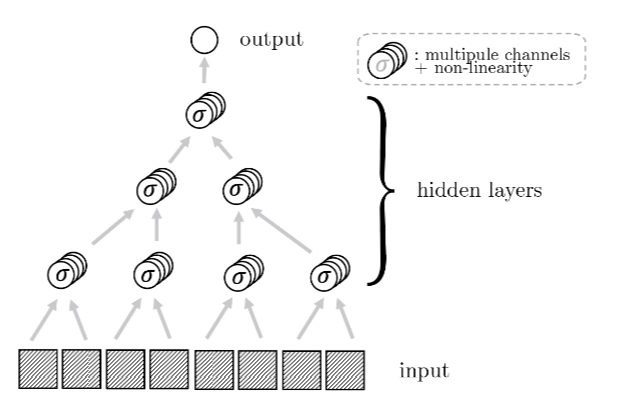
- Intuition: build a hierarchical representation mirroring the hierarchical structure.
- This representation is invariant to exchange of synonyms.
Takeaways
- Deep networks learn hierarchical tasks with a number of data polynomial in the input dimension
- They do so by developing internal representations that learn the hierarchical structure layer by layer
Application: generating novel data by probing hierarchical structure

- Goal: generate new data from existing ones
- At different levels of abstraction
Generative technique:
- Diffusion models: add noise + denoise
- Scale of change/features level depends on the noise amount
- Prediction: intermediate level of noise at which this scale is maximal (phase transition)
- Validated on images and text.
- What about proteins?
Diffusion on protein sequences
- Model for Discrete Diffusion: EvoDiff-MSA
- Dataset: J-Domain proteins
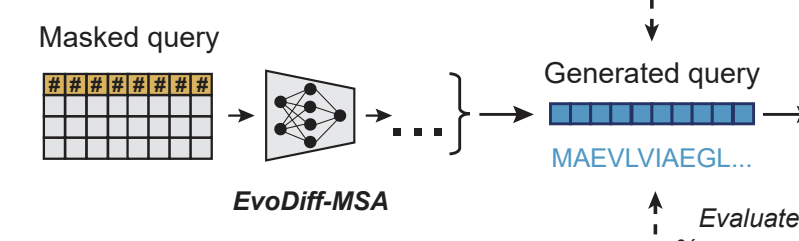
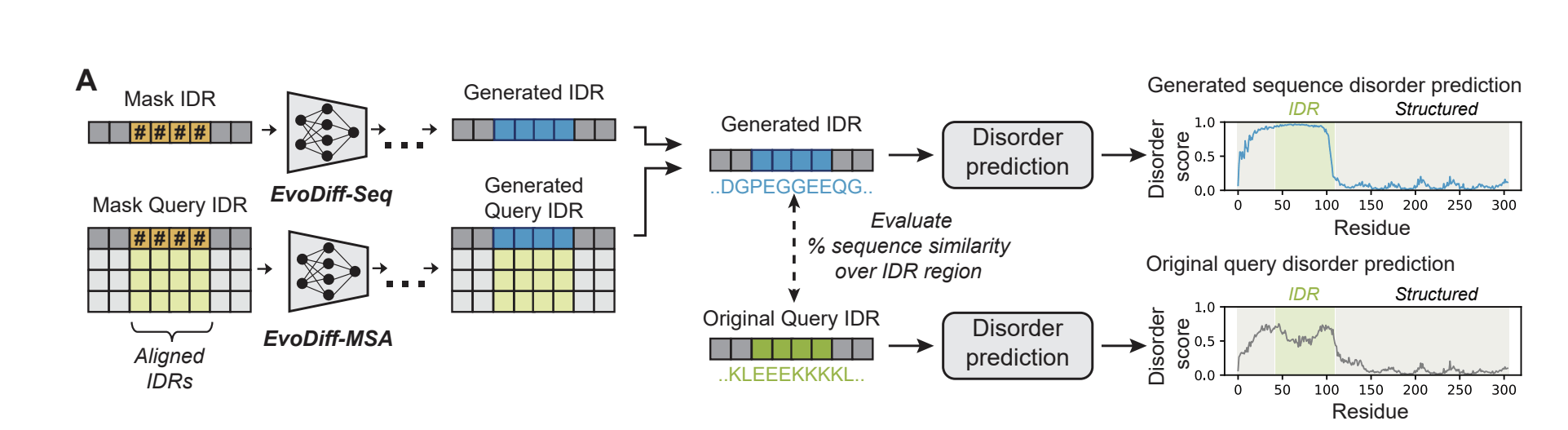
- Note: Can be used to generate Intrinsically Disordered Regions (IDR) conditioning on structured regions
- Generate new sequences by adding noise to protein sequence+denoising
- Do not find a phase transition in the amount of change wrt noise
- Uniform change along whole sequence
- Not consistent with hierarchical structure
-
Future investigations:
- Better model
- Structure 3D space

Are protein sequences hierarchical?
Umberto Tomasini - LLM
By umberto_tomasini
Umberto Tomasini - LLM
- 7



