Intertemporal Choice
Christopher Makler
Stanford University Department of Economics
Econ 50: Lecture 11
pollev.com/chrismakler
What song about time is playing right now?
This week: financial economics
Time
Risk
How much are we willing to give up now to have more later?
How much are we willing to pay to mitigate risks?
TODAY
WEDNESDAY
Applications
Inflation
Insurance
Portfolios
FRIDAY
Exercises 5.1, 5.2
Exercises 5.4, 5.5 (Q)
Exercise 5.3, poss. 5.6
I will also be posting a collection of old exam questions later today; solutions to be posted on Friday
Approach: Use Tools of Consumer Theory
- Assume there is some "value function" for consumption \(v(c)\)
- Sort of like an indirect utility function
- Create "utility functions" out of this value function
- Endowment budget constraint: instead of starting with some amount of money \(m\), we're going to start out with a bundle representing an income stream
- Buying/selling becomes borrowing/lending
Budget Constraint
Preferences
Functional forms for utility / value functions:
u(x_1,x_2) = av(x_1) + bv(x_2)
v(x) = \ln x
v(x) = \sqrt{x}
v(x) = x
v(x) = x^2
u(x_1,x_2) = a \ln x_1 + b \ln x_2
u(x_1,x_2) = a \sqrt{x_1} + b\sqrt{x_2}
u(x_1,x_2) = ax_1 + bx_2
u(x_1,x_2) = ax_1^2 + bx_2^2
Cobb-Douglas (decreasing MRS)
Weak Substitutes (decreasing MRS)
Perfect Substitutes (constant MRS)
Concave (increasing MRS)
Today's Agenda
- Modeling present-future tradeoffs
- The intertemporal budget constraint
- Preferences over time
- Optimal saving and borrowing
- Different interest rates for borrowing and saving
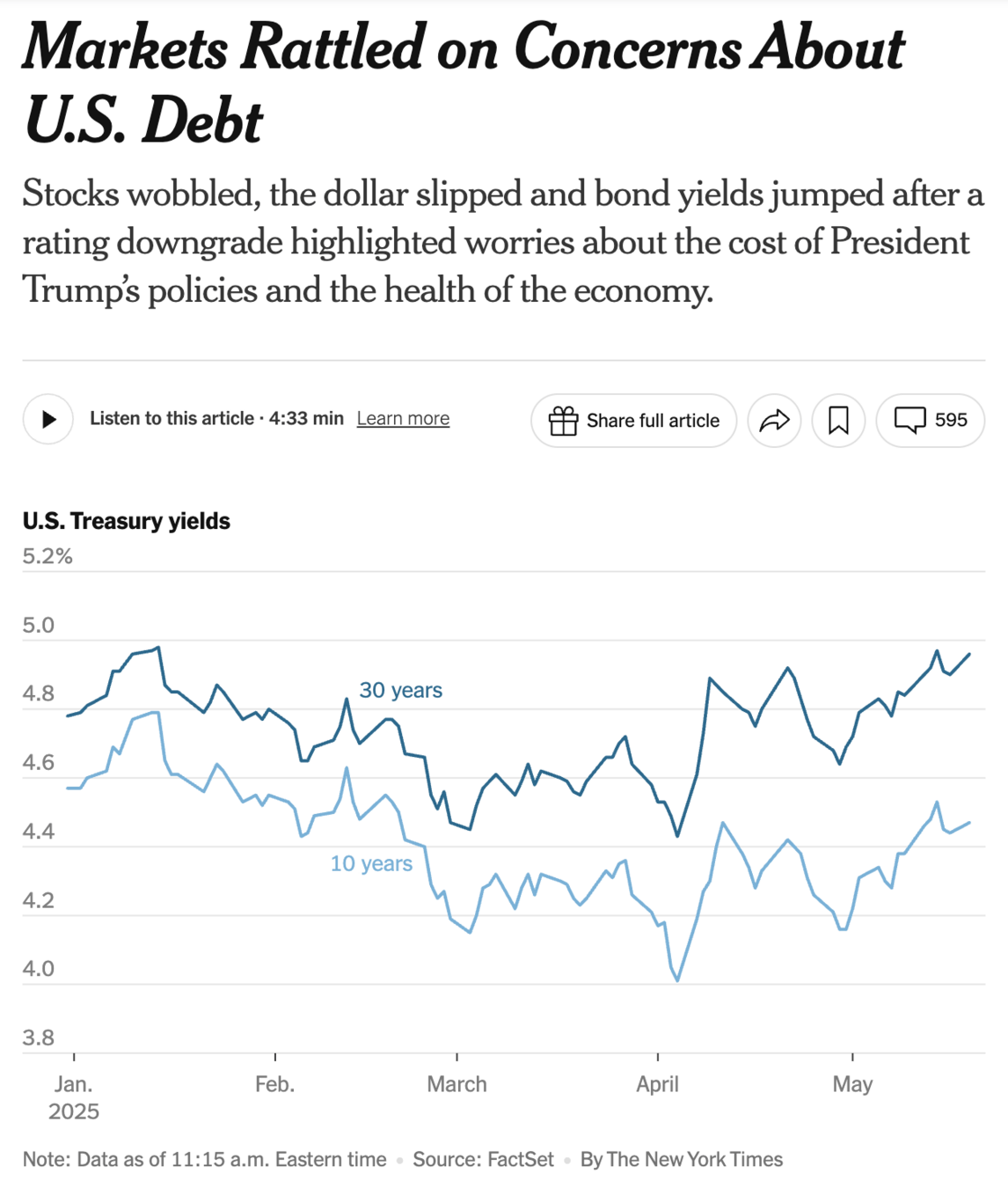
Saving and borrowing is a huge part of the economy.
Budget Line
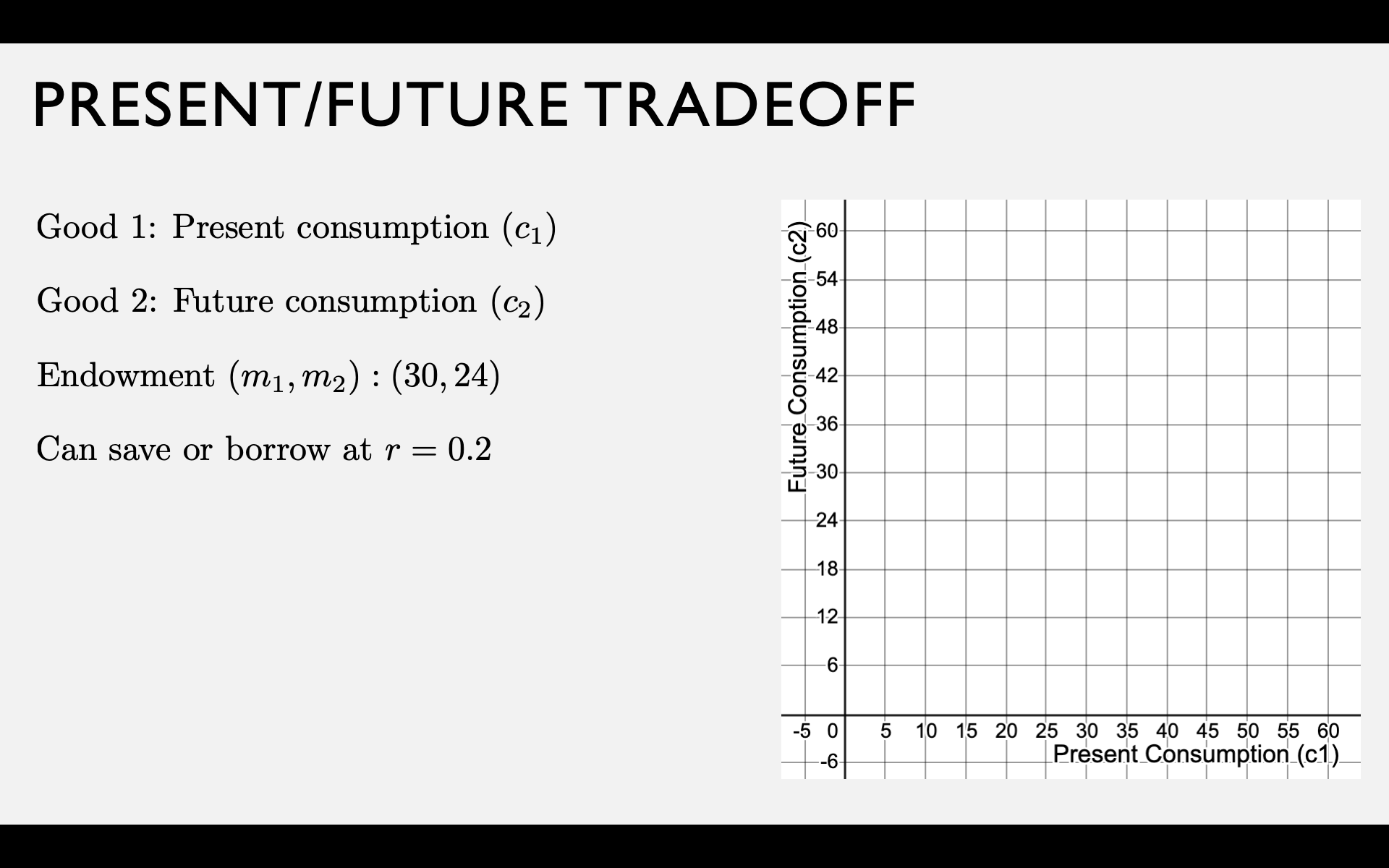
Present-Future Tradeoff
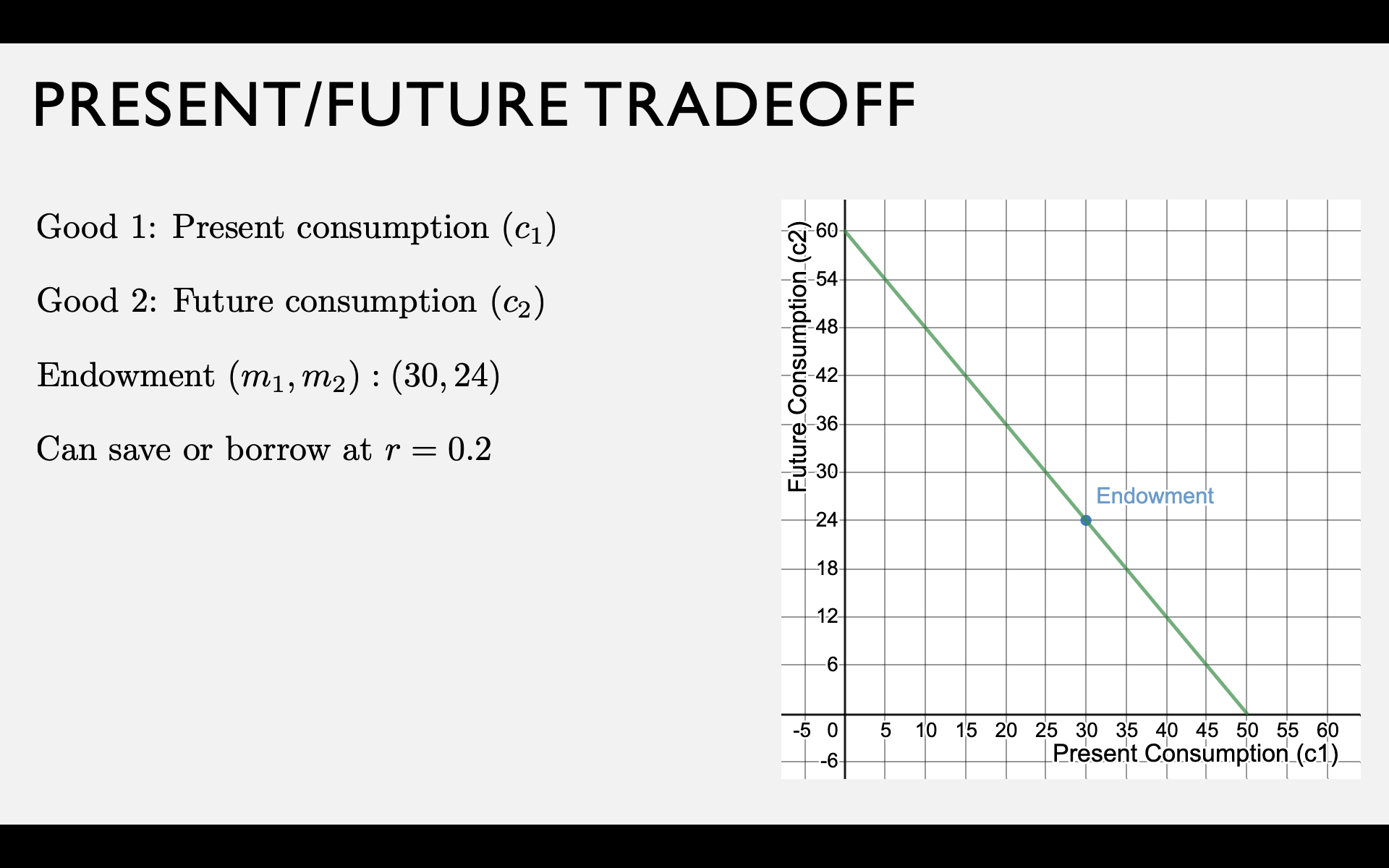
Your endowment is an income stream of \(m_1\) dollars now and \(m_2\) dollars in the future.
What happens if you don't consume all \(m_1\) of your present income?
Two "goods" are present consumption \(c_1\) and future consumption \(c_2\).
c_1 = m_1 - s
c_2 = m_2 + s
Let \(s = m_1 - c_1\) be the amount you save.
Saving and Borrowing with Interest
If you save at interest rate \(r\),
for each dollar you save today,
you get \(1 + r\) dollars in the future.
You can either save some of your current income, or borrow against your future income.
If you borrow at interest rate \(r\),
for each dollar you borrow today,
you have to repay \(1 + r\) dollars in the future.
c_1 = m_1 - s
c_2 = m_2 + (1+r)s
c_2 = m_2 + (1+r)(m - c_1)
(1+r)c_1 + c_2 = (1+r)m_1 + m_2
c_1 = m_1 + b
c_2 = m_2 - (1+r)b
c_2 = m_2 - (1+r)(c_1 - m_1)
(1+r)c_1 + c_2 = (1+r)m_1 + m_2
(1+r)c_1 + c_2 = (1+r)m_1 + m_2
How much can you consume in the future if you save all your present income \(m_1\)?
How much can you consume in the present if you borrow the maximum amount against your future income?
FV = c_2 = (1+r)m_1 + m_2
\displaystyle{PV = c_1 = m_1 + {m_2 \over 1 + r}}
c_1 + \frac{c_2}{1+r} = m_1 + \frac{m_2}{1 + r}
"Present Value"
c_1 + \frac{c_2}{1.2} = 30 + \frac{24}{1.2}
c_1 + \frac{c_2}{1.2} = 50
Preferences
Preferences over Time
u(c_1,c_2) = v(c_1)+\beta v(c_2)
v(c) = \text{“within-period" utility}
\beta = \text{“between-period" discount factor}
v(c) = \ln c
v(c) = c
u(c_1,c_2) = \ln c_1 + \beta \ln c_2
Examples:
v(c) = \sqrt{c}
u(c_1,c_2) = c_1 + \beta c_2
u(c_1,c_2) = \sqrt{c_1} + \beta \sqrt{c_2}
When to borrow and save?
u(c_1,c_2) = v(c_1)+\beta v(c_2)
MRS \text{ at endowment }= {v^\prime (m_1) \over \beta v^\prime (m_2)}
Save if MRS at endowment < \(1 + r\)
Borrow if MRS at endowment > \(1 + r\)
(high interest rates or low MRS)
(low interest rates or high MRS)
If we assume \(v(c)\) exhibits diminishing marginal utility:
MRS is higher if you have less money today (\(m_1\) is low)
and/or more money tomorrow (\(m_2\) is high)
MRS is lower if you are more patient (\(\beta\) is high)
u(c_1,c_2) = v(c_1)+\beta v(c_2)
MRS \text{ at endowment }= {v^\prime (m_1) \over \beta v^\prime (m_2)}
Save if MRS at endowment < \(1 + r\)
Borrow if MRS at endowment > \(1 + r\)
pollev.com/chrismakler
MRS(c_1,c_2) = {c_2 \over \beta c_1}
\text{Example: }v(c_t) = \ln c_t
u(c_1,c_2) = \ln c_1 + \beta \ln c_2
If \(m_1 = 30\), \(m_2 = 24\), and \(\beta = 0.5\),
what is the highest interest rate at which you would borrow money?
Borrow or Save?
MRS(c_1,c_2) = {c_2 \over \beta c_1}
\text{MRS at endowment } =
\text{Price Ratio } =
\text{Example: }v(c_t) = \ln c_t \Rightarrow u(c_1,c_2) = \ln c_1 + \beta \ln c_2
m_1 = 30, m_2 = 24, \beta = 0.5
\text{Generic }m_1,m_2,r
\text{Borrow if } :
MRS(m_1,m_2) = {m_2 \over \beta m_1}
MRS(30,24) = {24 \over 0.5 \times 30}
1 + r
= 1.6
>
1 + r
1.6
>
1 + r
MRS
r < 0.6
1 + r
Optimal Choice
Optimal Bundle
\text{Example: }v(c_t) = \ln c_t \Rightarrow u(c_1,c_2) = \ln c_1 + \beta \ln c_2
Tangency condition:
Budget line:
MRS(c_1,c_2) = {c_2 \over \beta c_1}
{c_2 \over \beta c_1} = 1 + r
(1 + r)c_1 + c_2 = (1 + r)m_1 + m_2
\Rightarrow c_2 = (1+r)\beta c_1
(1 + r)c_1 + (1+r)\beta c_1 = (1 + r)m_1 + m_2
c_1^* = {1 \over 1 + \beta}(m_1 + {m_2 \over 1 + r})
c_2^* = {\beta \over 1 + \beta}((1 + r)m_1 + m_2)
If \(m_1 = 30\), \(m_2 = 24\), \(\beta = 0.25\), and \(r = 0.2\),
what is your optimal choice?
pollev.com/chrismakler
Optimal Bundle
\text{Example: }v(c_t) = \ln c_t \Rightarrow u(c_1,c_2) = \ln c_1 + \beta \ln c_2
Tangency condition:
Budget line:
m_1 = 30, m_2 = 24, \beta = 0.25, r = 0.2
{c_2 \over \beta c_1} = 1 + r
{c_2 \over 0.25 c_1} = 1.2
(1 + r)c_1 + c_2 = (1 + r)m_1 + m_2
1.2c_1 + c_2 = 1.2 \times 30 + 24
1.2c_1 + c_2 = 60
\Rightarrow c_2 = 0.3 c_1
\Rightarrow c_2 = (1+r)\beta c_1
(1 + r)c_1 + (1+r)\beta c_1 = (1 + r)m_1 + m_2
1.2c_1 + 0.3 c_1 = 60
c_1^* = {1 \over 1 + \beta}(m_1 + {m_2 \over 1 + r})
c_2^* = {\beta \over 1 + \beta}((1 + r)m_1 + m_2)
c_1^* = 40
Since you start with \(m_1 = 30\), this means you borrow 10.
MRS(c_1,c_2) = {c_2 \over \beta c_1}
Supply and Demand
Supply of Savings and
Demand for Borrowing
Gross demand = your optimal bundle given interest rate \(r = (c_1^*(r), c_2^*(r))\)
If you want to consume more than your present income at interest rate \(r\),
your demand for borrowing is
\(b(r) = c_1^*(r) - m_1\)
How does this compare to your initial income stream \((m_1,m_2)\)?
If you want to consume less than your present income at interest rate \(r\),
your supply of savings is
\(s(r) = m_1 - c_1^*(r)\)
Different Interest Rates
MRS > 1 + r
MRS < 1 + r
BORROW
SAVE
What if the interest rate is different for borrowing and saving?
Summary
- No new math! We applied the math we've already developed to a new (and important) problem.
- Notion of net demand and net supply: where do you want to trade to from your endowment?
Econ 50 | Fall 25 | Lecture 11
By Chris Makler
Econ 50 | Fall 25 | Lecture 11
We apply the framework of consumer choice theory to the choice of how to allocation money across time, investigating saving and borrowing.
