Geometry

計算幾何

Ian Wen

INDEX

座標與向量

 

有向面積

線段相交

點到線段距離

極角排序

凸包演算法 (Monotone Chain)

特別感謝一三學術長 AaW 的簡報

 

什麼是計算幾何?

用電腦解幾何問題!

  1. 注意精度，不到最後關頭不使用浮點數
  2. 使用向量，不要硬算
  3. 小心實作

Template

計算幾何模板 (今天教的所有東西都在裡面)

 

#define X first
#define Y second
#define eps 1e-12
// #define double long long
typedef pair<double, double> pdd;
 
pdd operator+(pdd a, pdd b) 
{ return pdd(a.X + b.X, a.Y + b.Y); }
pdd operator-(pdd a, pdd b) 
{ return pdd(a.X - b.X, a.Y - b.Y); }
pdd operator*(pdd a, double b)
{ return pdd(a.X*b, a.Y*b); }
pdd operator/(pdd a, double b)
{ return pdd(a.X/b, a.Y/b); }
 
inline bool operator == (const pdd &a, const pdd &b){
    if(abs(a.X-b.X) <= eps && abs(a.Y - b.Y) <= eps) return true;
    return false;
}
 
double dot(pdd a, pdd b)
{ return a.X*b.X + a.Y*b.Y; }
double cross(pdd a, pdd b)
{ return a.X*b.Y - a.Y*b.X; }
double abs2(pdd a) // Square
{ return dot(a, a); }
double abs(pdd a)
{ return sqrt(dot(a, a)); }
 
int sign(double a)
{ return fabs(a) < eps ? 0 : a > 0 ? 1 : -1; }
int ori(pdd a, pdd b, pdd c)
{ return sign(cross(b - a, c - a)); }
 
bool collinearity(pdd p1, pdd p2, pdd p3) { // 三點共線
    return sign(cross(p1 - p3, p2 - p3)) == 0;
}
 
bool btw(pdd p1, pdd p2, pdd p3) { // p3 是否在 p1 p2 線段上
    if (!collinearity(p1, p2, p3)) { return 0; }
    else { return sign(dot(p1 - p3, p2 - p3)) <= 0; }
}
 
bool banana(pdd p1, pdd p2, pdd p3, pdd p4) {
    int a123 = ori(p1, p2, p3);
    int a124 = ori(p1, p2, p4);
    int a341 = ori(p3, p4, p1);
    int a342 = ori(p3, p4, p2);
    if (btw(p1, p2, p3) || btw(p1, p2, p4) || btw(p3, p4 ,p1) || btw(p3, p4, p2)) {
        return true;
    }
    else {
        return a123 * a124 < 0 && a341 * a342 < 0;
    }
}
 
pdd banana_point(pdd p1, pdd p2, pdd p3, pdd p4) {
    double a123 = cross(p2 - p1, p3 - p1);
    double a124 = cross(p2 - p1, p4 - p1);
    return (p4 * a123 - p3 * a124) / (a123 - a124);
}


int angle_type(pdd a, pdd o, pdd b) {
    double d = dot(a - o, b - o);
    return sign(d); // 0: 直角, >0: 銳角, <0: 鈍角
}

double pt_to_seg_dist(pdd a, pdd b, pdd k) {
    if (angle_type(a, b, k) > 0 && angle_type(b, a, k) > 0) {
        return fabs(cross(a - k, b - k)) / abs(b - a); // 投影在中間，算高
    }
    return sqrt(min(abs2(a - k), abs2(b - k))); // 投影不在線段上，取端點距離
}

pdd base;
bool angle_cmp(pdd a, pdd b) {
    a = a - base;
    b = b - base;
    bool f1 = (a.Y < 0 || (a.Y == 0 && a.X < 0)); // 判斷在 y < 0 的半平面
    bool f2 = (b.Y < 0 || (b.Y == 0 && b.X < 0));
    if (f1 != f2) return f1 < f2;
    return cross(a, b) > 0; // 逆時針順序
}

void angle_sort(vector<pdd>& pts, pdd origin) {
    base = origin;
    sort(pts.begin(), pts.end(), angle_cmp);
}

vector<pdd> convex_hull(vector<pdd> pts) {
    sort(pts.begin(), pts.end());
    vector<pdd> hull;
    for (int t=0; t<2; t++) { // 找下找上
        int sz = hull.size();
        for (pdd pt : pts) {
            while (hull.size() - sz >= 2 && ori(hull[hull.size()-2], hull.back(), pt) < 0) { // <= 0 忽略邊上的點 < 0 不忽略
                hull.pop_back(); // 單調維護
            }
            hull.push_back(pt);
        }
        hull.pop_back(); // 下凸包最後一點是上凸包的開頭
        reverse(pts.begin(), pts.end());
    }
    return hull;
}

座標與向量

座標

向量

向量運算

EPS

座標與向量

相信各位已經讀過課前預習了

文檔

座標與向量

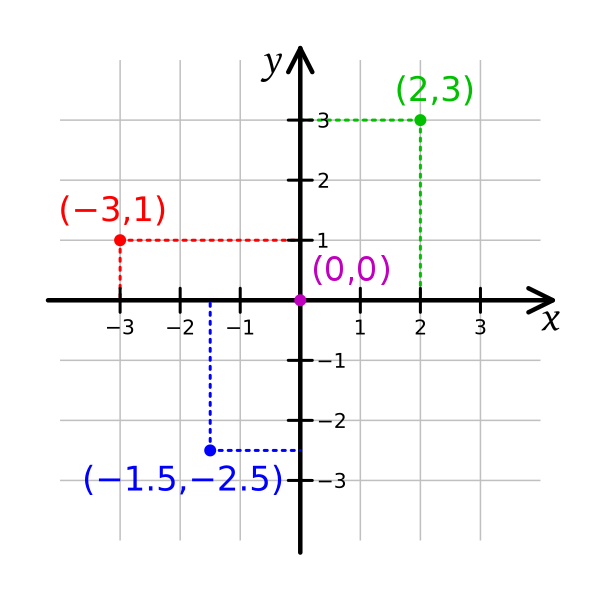
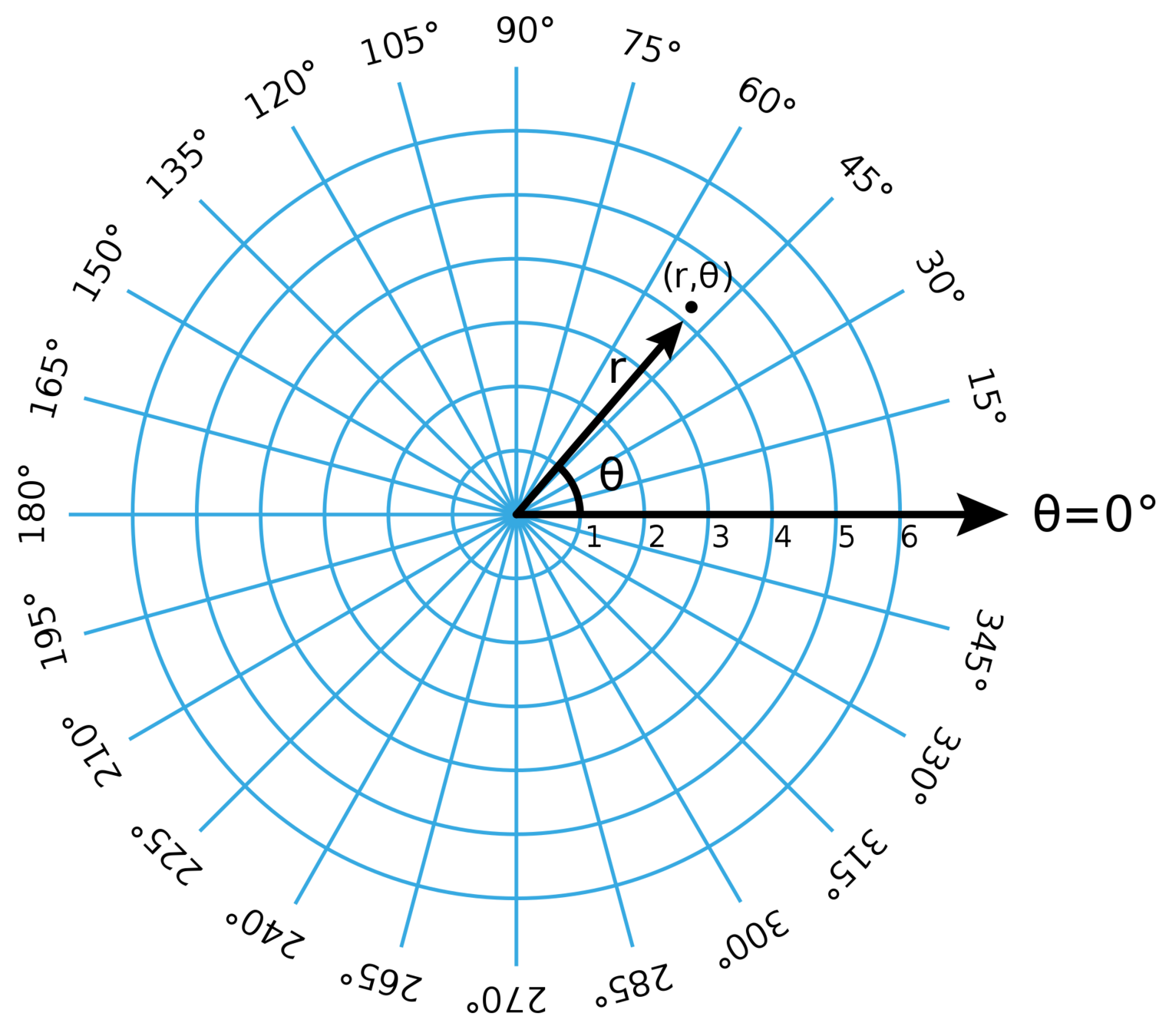
直角坐標系

\((x,\, y)\)

極坐標系

\((r,\, \theta)\)

座標與向量

向量

  • 有向線段（向：方向、量：長度）
  • 純量：只有大小、沒有方向的量
  • \(\overrightarrow{AB} \) ：由 A 點起始指向 B 點的向量
  • 可任意移動
  • 向量長度（加絕對值表示）：兩點的歐基里德距離


 

\(\left|\overrightarrow{AB}\right| = \sqrt{{(x_A - x_B)}^2 + {(y_A - y_B)}^2}\)

座標與向量

向量的運算

  • 向量加法 \(\vec a + \vec b\)
  • 向量減法 \(\vec a - \vec b\)
  • 向量外積 \(\vec a \times \vec b\)
  • 向量內積 \(\vec a \cdot \vec b\)

 

加減乘乘

座標與向量

向量的運算

加

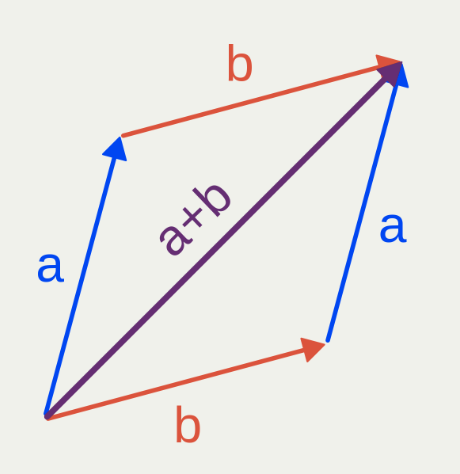
  • 頭尾相連：\( \overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC}\)
  • 在圖上可以用三角形法或平行四邊形法
  • 代數運算：
  • \( \overrightarrow{a} = (a_1, a_2) , \overrightarrow{b} = (b_1, b_2), \overrightarrow{c} = (c_1, c_2)\)
  • \( \overrightarrow{a} + \overrightarrow{b} = \overrightarrow{c}\)
    • \(\Rightarrow \, a_1+b_1= c_1\)
    • \(\Rightarrow \,a_2 + b_2 = c_2\)

座標與向量

向量的運算

減

加上反向向量

\(\overrightarrow{AB} - \overrightarrow{CD} = \overrightarrow{AB} + \overrightarrow{DC}\)

座標與向量

向量的運算

乘

分為三種

  1. 向量係數積：純量 * 向量 \(\rightarrow\)  向量
  2. 向量內積：　向量 \(\cdot\) 向量 \(\rightarrow\) 純量
  3. 向量外積：　向量 \(\times\) 向量 \(\rightarrow\) 向量

座標與向量

向量的運算

乘

分為三種

  1. 向量係數積：純量 * 向量 \(\rightarrow\)  向量
  2. 向量內積：　向量 \(\cdot\) 向量 \(\rightarrow\) 純量
  3. 向量外積：　向量 \(\times\) 向量 \(\rightarrow\) 向量

座標與向量

向量的運算

係數積

若 \(\vec A = (x, y)\)

\(k\) 為純量

則 \(k\vec A = (kx, ky)\)

幾何意義：

將向量長度放大 k 倍

座標與向量

向量的運算

內積 Dot Product

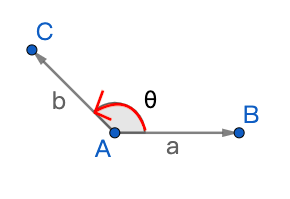
定義：若 \(\vec a\) 與 \(\vec b\) 為二度或三度空間的向量，且 \(\theta\) 為 \(\vec a\) 與 \(\vec b\) 的夾角（滿足\(0\leq\theta\leq\pi\)），

則點積 \(\vec a\cdot\vec b\) 定義為

a\cdot b= \begin{cases} |a||b|\cos\theta& ,a ≠ 0\land b ≠ 0\\ 0& a = 0\lor b = 0 \end{cases}

座標與向量

向量的運算

內積 Dot Product

  • 直觀看法：兩個向量在「同一方向」的程度
  • 兩個向量的內積（點積）以「\(\cdot\)」表示
  • 運算結果為一個純量
  • 幾何關係：\(\vec A\cdot \vec B = |\vec A||\vec B|\cos\theta\)
  • 正定性：\(|\vec A|^2 = \vec A\cdot\vec A\)
  • 座標公式：假設\(A(x_A,y_A),B(x_B,y_B)\)，則內積滿足：\(\vec A\cdot\vec B = x_Ax_B+y_Ay_B\)
  • 怎麼證明這兩個公式相等？
  • 將cos用餘弦定理代換！

座標與向量

向量的運算

內積 Dot Product

  1. \(\vec A\cdot\vec B > 0\)：兩向量之間的夾角為銳角
  2. \(\vec A\cdot\vec B = 0\)：兩向量垂直
  3. \(\vec A\cdot\vec B < 0\)：兩向量夾角為鈍角

座標與向量

向量的運算

外積 Cross Product

定義：若\(a = (a_1,a_2,a_3)\)與\(b = (b_1,b_2,b_3)\)為三度空間裡的向量，則外積（叉積）\(a\times b\) 為一向量定義為：

a\times b = (\left |\begin{matrix}a_2 &a_3\\b_2 &b_3 \\\end{matrix} \right | ,\left |\begin{matrix}a_3&a_1\\b_3 &b_1 \\\end{matrix} \right | ,\left |\begin{matrix}a_1&a_2\\b_1 &b_2 \\\end{matrix} \right | )

向量的外積只有在三度空間才有定義！

外積結果的向量由右手定則決定

座標與向量

向量的運算

外積 Cross Product

  • 直觀看法：兩向量在逆時針方向的「垂直」的程度
  • 兩個向量的外積（叉積）以「\(\times\)」表示
  • 幾何關係：\(\vec A\times \vec B = \hat n|\vec A||\vec B|\sin\theta\)（\(\theta\)為有向角）
  • 運算結果為一個向量（三維空間），方向由右手定則決定
  • 外積結果同時也是兩向量所張的平行四邊形面積，我們在二維平面上將它拿來當作純量來使用
  • 座標公式：假設\(A(x_A,y_A),B(x_B,y_B)\)，則外積滿足：\(|\vec A\times\vec B| = x_Ay_B-x_By_A\)

座標與向量

向量的運算

外積 Cross Product

  1. \(\vec A\times\vec B > 0\)：A向量到B向量逆時針旋轉
  2. \(\vec A\times\vec B = 0\)：兩向量平行
  3. \(\vec A\times\vec B < 0\)：A向量到B向量順時針旋轉

座標與向量

向量的運算

內積 vs 外積

  • 向量內積（Dot Product）
    • 判斷向量是否垂直
    • 結果為純量
  • 向量外積（Cross Product）
    • 判斷向量是否平行
    • 結果為向量（今天都當純量來用）
    • 判斷向量夾角方向 （順時針或是逆時針）
    • 可用來計算面積

座標與向量

向量的運算

Implement

座標也可以用一樣的方式實作，例如：

\(A\)點的座標可以視為\(\overrightarrow{OA}\) 來處理

#define X first
#define Y second
#define eps 1e-12
// #define double long long
typedef pair<double, double> pdd;
 
pdd operator+(pdd a, pdd b) 
{ return pdd(a.X + b.X, a.Y + b.Y); }
pdd operator-(pdd a, pdd b) 
{ return pdd(a.X - b.X, a.Y - b.Y); }
pdd operator*(pdd a, double b)
{ return pdd(a.X*b, a.Y*b); }
pdd operator/(pdd a, double b)
{ return pdd(a.X/b, a.Y/b); }
inline bool operator == (const pdd &a, const pdd &b){
    if(abs(a.X-b.X) <= eps && abs(a.Y - b.Y) <= eps) return true;
    return false;
}
 
double dot(pdd a, pdd b)
{ return a.X*b.X + a.Y*b.Y; }
double cross(pdd a, pdd b)
{ return a.X*b.Y - a.Y*b.X; }
double abs2(pdd a) // Square
{ return dot(a, a); }
double abs(pdd a)
{ return sqrt(dot(a, a)); }

座標與向量

向量的運算

什麼是 eps

  • 在進行有小數的計算幾何時，常常會有很多的 "浮點誤差"
  • eps為誤差容忍值
  • 兩數相差eps內視爲相等

\(x ⇒ (x − eps, x + eps)\)

inline bool operator == (const pdd &a, const pdd &b){
    if(abs(a.X-b.X) <= eps && abs(a.Y - b.Y) <= eps) return true;
    return false;
}

有向面積

性質

Pick's Theorem

題目

 

有向面積

  • 利用外積計算多邊形面積
  • 有向角：逆時針為正、順時針為負
  • 外積有正有負，稱為「有向面積」

+

-

有向面積

可以幹嘛？

  1. 計算面積

  2. 評估角度

有向面積

兩向量夾出的三角形有向面積為：

\triangle ABC = \frac{1}{2} \overrightarrow{AB}\times \overrightarrow{AC}

A

B

C

有向面積

多邊形面積

  1. 在平面上任選一點（通常是原點）
  2. 以此點為一端點，將多邊形切割成許多三角形。
  3. 依照逆時鐘的方向將所有三角形的有向面積相加即是多邊形的有向面積。

Source: https://reurl.cc/NZ5ZNq

有向面積

多邊形面積

假設多邊形的頂點依序為（要特別注意結束的點必須是起始點）：

P_0,P_1,...,P_{n-1},P_n = P_0

則多邊形的面積為（aka測量師公式）：

AREA = \frac{1}{2}|\sum_{i = 0}^{n-1}{\overrightarrow{P_i}\times \overrightarrow{P_{i+1}}}|

有向面積

多邊形面積

有向面積

Pick's Theorem

給定頂點座標均是格子點的簡單多邊形，皮克定理說明了其面積\(A\)和內部格點數目\(i\)、邊上格點數目\(b\)的關係：

A = i + \frac{b}{2} - 1

證明在這裡

有向面積

Pick's Theorem - 舉例

A = i + \frac{b}{2} - 1
\textcolor{white}{A = 10} \\\textcolor{red}{i = 7} \\\textcolor{blue}{B = 8}

有向面積

Pick's Theorem - 舉例

A = i + \frac{b}{2} - 1
\textcolor{white}{A = 10} \\\textcolor{red}{i = 7} \\\textcolor{blue}{B = 8}

有向面積

題目

 

線段相交 (banana)

如何判斷

方向函式

點與線段的關係

蕉點座標

線段香蕉應用

banana

二元一次方程式求交點

看有沒有解

更快的做法？

直線法向量

若一直線 \(ax+by = c\)

則其法向量為 (a, b)

法向量方向與直線垂直

proof ? 畫看看

已知兩直線法向量，

可透過法向量是否平行得知兩向量有沒有焦點

如何判斷兩個直線是否香蕉？

如何判斷兩個線段是否香蕉？

直接求出直線交點，再判斷交點是否在線段內

這樣好嗎？
聽起來很麻煩誒

求交點的問題

  • 沒有交點？
  • 無限多交點？
  • 交點不好求 e.g. 垂直線
  • 交點位置誤差？

banana

方向函式 ori

  • 利用外積找兩向量相對的方向，方便判斷
  • 共線則為回傳0，逆時針回傳1，順時針回傳-1
//方向函數ori，回傳ab向量與ac向量的方向
int sign(double a)
{ return fabs(a) < eps ? 0 : a > 0 ? 1 : -1; }

int ori(pdd a, pdd b, pdd c)
{ return sign(cross(b - a, c - a)); }

banana

方向函式 ori

方向函式能做什麼？

判斷點是否在線段兩端點的異側！

banana

更精準的求線段相交

若線段 \(AB\) 與線段 \(CD\)  相交

則點 \(C\) 和 \(D\) 會在線段 \(AB\) 異側

且 點 \(A\) 和 \(B\) 會在線段 \(CD\) 異側

ori(C,D,A)\times ori(C,D,B) <= 0

＝0代表C或D有一點在直線 AB 上面

ori(A,B,C)\times ori(A,B,D) <= 0

banana

特判情形

線段端點在另一線段上

  • 判斷線段香蕉之前，先處理點在線段上的情況
  • btw() 判斷點 O 是否在 AB 之間
  • 當點在線段上時，OA向量與OB向量之外積為零、內積為負（夾角為180度）
bool btw(pdd p1, pdd p2, pdd p3) { // p3 是否在 p1 p2 線段上
    if (!collinearity(p1, p2, p3)) { return 0; }
    else { return sign(dot(p1 - p3, p2 - p3)) <= 0; }
}

banana

完整的線段相交

  • 首先判斷特例，也就是線段有一端點在另外線段上
  • 利用方向函式判斷點是否在另一線段端點的異側
bool banana(pdd p1, pdd p2, pdd p3, pdd p4) {
    int a123 = ori(p1, p2, p3);
    int a124 = ori(p1, p2, p4);
    int a341 = ori(p3, p4, p1);
    int a342 = ori(p3, p4, p2);
    if (btw(p1, p2, p3) || btw(p1, p2, p4) || btw(p3, p4 ,p1) || btw(p3, p4, p2)) {
        return true;
    }
    else {
        return a123 * a124 < 0 && a341 * a342 < 0;
    }
}

banana

蕉點

知道兩線段是否相交之後，進一步求出交點座標

\vec{P} = \vec{A} + t\overrightarrow{AB}

banana

蕉點

幾個算式列一列得到：

t = \frac{\overrightarrow{CA}\times\overrightarrow{CD}}{\overrightarrow{CD}\times\overrightarrow{AB}}

帶回 \(\vec{P} = \vec{A} + t\overrightarrow{AB}\) 即可

pdd banana_point(pdd p1, pdd p2, pdd p3, pdd p4) {
    double a123 = cross(p2 - p1, p3 - p1);
    double a124 = cross(p2 - p1, p4 - p1);
    return (p4 * a123 - p3 * a124) / (a123 - a124);
}

banana

香蕉應用

Point in Polygon

給定平面上\(n\)個點構成的簡單多邊形，還有\(m\)個詢問的點。對每一個點輸出它是在多邊形內部、外部或邊界上。

 

$$3\leq n\leq 1000$$

$$1\leq m\leq 1000$$

$$10^9\leq x_i,y_i\leq 10^9$$

banana

來看看凸多邊形的情況

  • 由P點指向多邊形上點的向量依序繞一圈做外積，過程中結果皆為正，表示在多邊形內部。
  • 若遇到凹多邊形，則這個方法會失敗。

banana

射線做法

  • 對每一個點做一條往正x方向的射線（實作上就是和一個x座標很大的點，連成線段）
  • 計算每一條邊與這條線段相交的次數。
  • 如果是奇數則在多邊形內部，反之則是在外部。
  • 小心處理相交於多邊形頂點的情況
    • 頂點會被算到兩次
    • 相交頂點時只考慮 \(y\) 較小的點
    • 把射線改成往右上角斜？
    • 右端點設成\((\infty,y_i+1)\)

banana

題目

 

banana

點到線距離

問 C 點到 \(\overline{\rm AB}\) 的距離平方

  • 當ABC皆為格子點時，此平方必為有理數

Case - 1

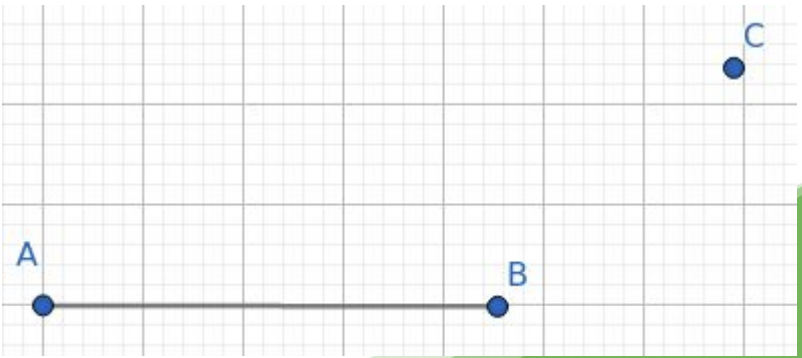
垂足在外面

\(\min(\rm |C-A|, |C-B|)\)

Case - 2

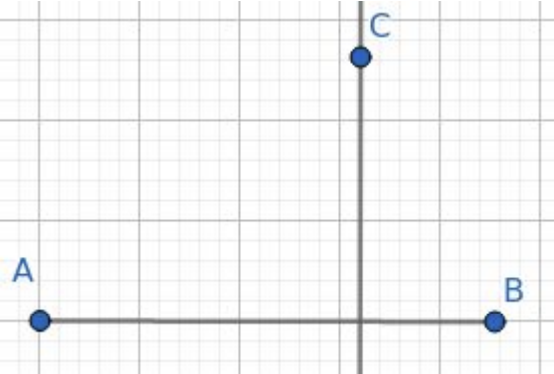
垂足在線段上

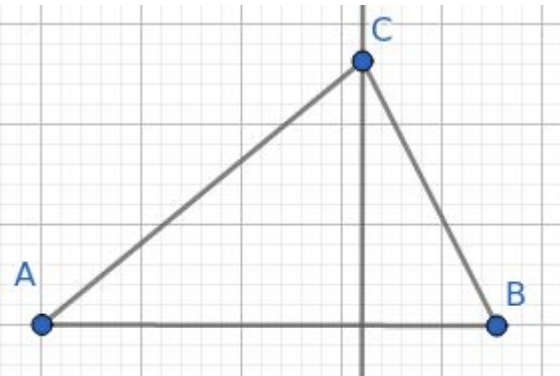
用面積以及底邊長度求高！

所以到底怎麼判垂足在哪？

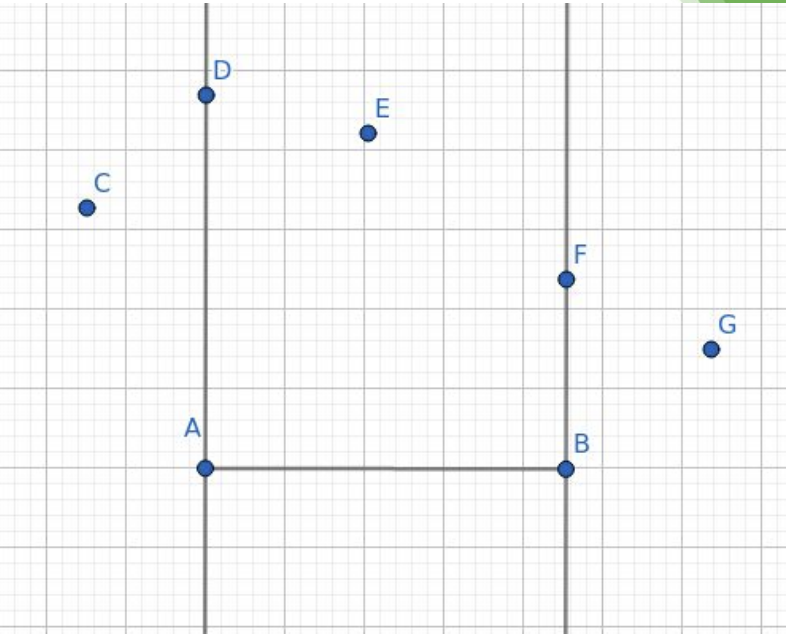
\(\angle CAB\) 和 \(\angle CBA\) 都是銳角時，長度為高！

 銳角? 用內積！

實作

int angle_type(pdd a, pdd o, pdd b) {
    double d = dot(a - o, b - o);
    return sign(d); // 0: 直角, >0: 銳角, <0: 鈍角
}

double pt_to_seg_dist(pdd a, pdd b, pdd k) {
    if (angle_type(a, b, k) > 0 && angle_type(b, a, k) > 0) {
        return fabs(cross(a - k, b - k)) / abs(b - a); // 投影在中間，算高
    }
    return sqrt(min(abs2(a - k), abs2(b - k))); // 投影不在線段上，取端點距離
}

極角排序

Polar coordinate system

利用每一個對特定點（通常是原點）的極座標的角度進行排序

應用範圍

  • 點集共線問題
  • 點集能構成多少個三角形
  • 常常搭配雙指針找範圍

Sort by Cross

  • 利用有向角的正負決定前後順序
  • 因為外積的夾角都是較小的角，不能直接Cross，要先判斷點在左或右半平面
pdd base;
bool angle_cmp(pdd a, pdd b) {
    a = a - base;
    b = b - base;
    bool f1 = (a.Y < 0 || (a.Y == 0 && a.X < 0)); // 判斷在 y < 0 的半平面
    bool f2 = (b.Y < 0 || (b.Y == 0 && b.X < 0));
    if (f1 != f2) return f1 < f2;
    return cross(a, b) > 0; // 逆時針順序
}

void angle_sort(vector<pdd>& pts, pdd origin) {
    base = origin;
    sort(pts.begin(), pts.end(), angle_cmp);
}

TIOJ 1205 - 直角三角形

  • 枚舉三角形的三個頂點，排除三點共線的情況，檢查兩兩線段夾的角度是不是直角。
    • 複雜度：\(O(n^3)\)
    • 可能會TLE，但時限7秒會過
  • 極角排序？
    • 枚舉每一個點當作原點，對所有點進行極角排序
    • 預處理將所有共線的點縮成一點，紀錄共線數
    • 雙指針走訪每一個點，與原點夾90度則答案加上共線數
    • 繞完一圈就結束了！
    • 複雜度：\(O(n^2\log n)\)

TIOJ 1205 - 直角三角形

#pragma GCC optimize("Ofast")
#pragma GCC optimize("fast-math","unroll-loops","no-stack-protector")

#include<bits/stdc++.h>
using namespace std;

#define pb push_back
#define ff first
#define ss second
#define rep(i, n) for(signed i=0; i<signed(n); i++)
#define all(x) x.begin(),x.end()
#define int long long

const int MOD = 1e9+7;
const int MAXN = 3e5+5;
const int PRIME = 712271227;
const int INF = 1000000005;
const long long INFF = 2e18;

#define X first
#define Y second
#define eps 1e-12

typedef pair<double, double> pdd;

pdd operator+(pdd a, pdd b) { 
    return pdd(a.X + b.X, a.Y + b.Y); 
}
pdd operator-(pdd a, pdd b) { 
    return pdd(a.X - b.X, a.Y - b.Y); 
}
pdd operator*(pdd a, double b) { 
    return pdd(a.X * b, a.Y * b); 
}
pdd operator/(pdd a, double b) { 
    return pdd(a.X / b, a.Y / b); 
}

inline bool operator==(const pdd &a, const pdd &b){
    return (fabs(a.X - b.X) <= eps && fabs(a.Y - b.Y) <= eps);
}

// 向量內積與外積
double dot(pdd a, pdd b) { return a.X * b.X + a.Y * b.Y; }
double cross(pdd a, pdd b) { return a.X * b.Y - a.Y * b.X; }
double abs2(pdd a){ return dot(a, a); }
double abs(pdd a){ return sqrt(dot(a, a)); }

int sign(double a){ 
    return fabs(a) < eps ? 0 : (a > 0 ? 1 : -1); 
}

// 幾何判斷：三點的定向
int ori(pdd a, pdd b, pdd c){ 
    return sign(cross(b - a, c - a)); 
}

// 以下函式在本題中未被使用，可以保留作其他用途
bool collinearity(pdd p1, pdd p2, pdd p3) { 
    return sign(cross(p1 - p3, p2 - p3)) == 0;
}
bool btw(pdd p1, pdd p2, pdd p3) { 
    if (!collinearity(p1, p2, p3)) return false;
    return sign(dot(p1 - p3, p2 - p3)) <= 0;
}
bool banana(pdd p1, pdd p2, pdd p3, pdd p4) {
    int a123 = ori(p1, p2, p3);
    int a124 = ori(p1, p2, p4);
    int a341 = ori(p3, p4, p1);
    int a342 = ori(p3, p4, p2);
    if (btw(p1, p2, p3) || btw(p1, p2, p4) || btw(p3, p4, p1) || btw(p3, p4, p2)) {
        return true;
    } else {
        return a123 * a124 < 0 && a341 * a342 < 0;
    }
}
pdd banana_point(pdd p1, pdd p2, pdd p3, pdd p4) {
    double a123 = cross(p2 - p1, p3 - p1);
    double a124 = cross(p2 - p1, p4 - p1);
    return (p4 * a123 - p3 * a124) / (a123 - a124);
}
int angle_type(pdd a, pdd o, pdd b) {
    double d = dot(a - o, b - o);
    return sign(d); // 0: 直角, >0: 銳角, <0: 鈍角
}
double pt_to_seg_dist(pdd a, pdd b, pdd k) {
    if (angle_type(a, b, k) > 0 && angle_type(b, a, k) > 0) {
        return fabs(cross(a - k, b - k)) / abs(b - a);
    }
    return sqrt(min(abs2(a - k), abs2(b - k)));
}

pdd base;
bool angle_cmp(pdd a, pdd b) {
    a = a - base;
    b = b - base;
    bool f1 = (a.Y < 0 || (a.Y == 0 && a.X < 0)); // 判斷在 y < 0 的半平面
    bool f2 = (b.Y < 0 || (b.Y == 0 && b.X < 0));
    if (f1 != f2) return f1 < f2;
    return cross(a, b) > 0; // 逆時針順序
}

void angle_sort(vector<pdd>& pts, pdd origin) {
    base = origin;
    sort(pts.begin(), pts.end(), angle_cmp);
}

// 想法：以某點 id 為直角頂點，統計構成直角三角形的組數
int solve(pdd id, const vector<pdd>& pts) {
    vector<pdd> temp;    // 存放以 id 為原點的向量集合
    vector<int> cnt;     // 存放同一方向上重合的點數量
    vector<pdd> pp;      // 壓縮共線後的唯一方向向量集合

    // 排除點 id 自身，其餘點轉換為以 id 為原點
    for (auto p : pts) {
        pdd cur = p - id;
        if(cur == pdd(0, 0)) continue;
        temp.push_back(cur);
    }

    // 依極角排序
    angle_sort(temp, pdd(0, 0));

    // 壓縮共線方向，只保留每個方向的一個向量，並記錄其重合數量
    pp.push_back(temp[0]);
    cnt.push_back(1);
    int len = temp.size();
    for (int i = 1; i < len; i++){
        double c = cross(temp[i], temp[i - 1]);
        double d = dot(temp[i], temp[i - 1]);
        // 如果兩向量共線且同向則合併計數
        if (fabs(c) <= eps && d >= -eps)
            cnt.back()++;
        else {
            pp.push_back(temp[i]);
            cnt.push_back(1);
        }
    }
    
    len = pp.size();
    // 為了處理極角跨圈的情況，將 pp 與 cnt 再複製一遍接在後面
    for (int i = 0; i < len; i++){
        pp.push_back(pp[i]);
        cnt.push_back(cnt[i]);
    }

    int ans = 0, p1 = 0;
    // 雙指針枚舉每個方向向量 pp[i]
    for (int i = 0; i < len; i++){
        // 以 pp[i] 為一邊，找另一邊與其垂直，即內積等於 0 且夾角為正向（外積 > 0）的方向
        while(p1 < i + len && sign(cross(pp[i], pp[p1])) >= 0 && dot(pp[i], pp[p1]) > eps)
            p1++;
        // 當找到滿足垂直條件的向量時，累計組合數量
        if(p1 < i + len && sign(cross(pp[i], pp[p1])) > 0 && fabs(dot(pp[i], pp[p1])) <= eps)
            ans += cnt[i] * cnt[p1];
    }
    return ans;
}
// #define FASTIO 
// #define AUTOIO

signed main() {
    #ifdef FASTIO
        ios::sync_with_stdio(0);cin.tie(0);
    #endif
    #ifdef AUTOIO
        freopen("input.txt", "r", stdin); 
        freopen("output.txt", "w", stdout); 
    #endif
    int n;
    while(cin >> n && n) {
        vector<pdd> pts(n);
        for (int i = 0; i < n; i++){
            cin >> pts[i].X >> pts[i].Y;
        }
        int answer = 0;
        // 遍歷所有點，統計以該點為直角頂點的直角三角形個數
        for (int i = 0; i < n; i++){
            answer += solve(pts[i], pts);
        }
        cout << answer << "\n";
    }
    return 0;
}

\(O(n^2\log n)\)

可以試著寫看看 \(O(n^3)\) 的做法

凸包演算法

找凸包的演算法有很多

找凸包的演算法有很多

  • Gift wrapping (a.k.a. Jarvis march)
  • Graham scan
  • Quickhull
  • Divide and conquer
  • Monotone chain (a.k.a. Andrew's algorithm)
  • Incremental convex hull algorithm
  • Kirkpatrick–Seidel algorithm
  • Chan's algorithm

凸包?

  • 凸包是一個凸多邊形（convex polygon）
  • 滿足內角都 ≤180≤180度的多邊形
  • 可以包住平面上所有點

單調鍊凸包

Monotone Chain

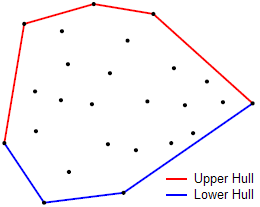
  • Monotone chain = 單調鍊
  • 凸包 = 下凸包 + 上凸包
  • 對點維護一個單調隊列
  • 解決了凸包有重疊的點、共線的點、退化成線段和點的情況。

單調鍊凸包

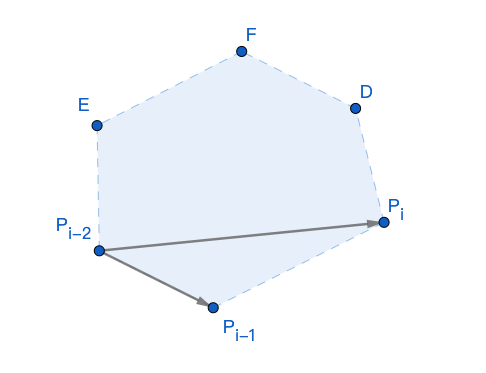
Monotone Chain

  1. 對所有點的座標由x由小排到大
  2. 使用一個vector（功能為stack）紀錄當前凸包
  3. 檢查新加入的點會讓vector中哪些點不再是凸包上的點：假設單調隊列中末兩個點是\(P_{i−2}\) , \(P_{i−1}\)，則如果新加入的點 \(P_i\)​ 為凸包上的一點，則滿足：

把下半部凸包圍起來，

上半部也可以照同樣方式圍出來。

\overrightarrow{P_{i-2}P_{i-1}} \times \overrightarrow{P_{i-2}P_{i}} > 0

4. 對點逆序之後把上凸包圍出來

單調鍊凸包

Monotone Chain

\overrightarrow{P_{i-2}P_{i-1}} \times \overrightarrow{P_{i-2}P_{i}} > 0

單調鍊凸包

Monotone Chain

單調鍊凸包

Monotone Chain

單調鍊凸包

Monotone Chain

單調鍊凸包

Monotone Chain

單調鍊凸包

Monotone Chain

單調鍊凸包

Monotone Chain

單調鍊凸包

Monotone Chain

將所有點reverse圍上凸包！

單調鍊凸包

Monotone Chain

單調鍊凸包

Monotone Chain

單調鍊凸包

Monotone Chain

單調鍊凸包

Monotone Chain

單調鍊凸包

Monotone Chain

單調鍊凸包

Monotone Chain

好欸，做完了！

單調鍊凸包

Monotone Chain

好欸，做完了！

單調鍊凸包

Monotone Chain

vector<pdd> convex_hull(vector<pdd> pts) {
    sort(pts.begin(), pts.end());
    vector<pdd> hull;
    for (int t=0; t<2; t++) { // 找下再找上
        int sz = hull.size();
        for (pdd pt : pts) {
            while (hull.size() - sz >= 2 && ori(hull[hull.size()-2], hull.back(), pt) < 0) { // <= 0 忽略邊上的點 < 0 不忽略
                hull.pop_back(); // 單調維護
            }
            hull.push_back(pt);
        }
        hull.pop_back(); // 下凸包最後一點是上凸包的開頭
        reverse(pts.begin(), pts.end());
    }
    return hull;
}

單調鍊凸包

Monotone Chain

教完了 掰

段考即將炸裂的

Ian Wen

Made with Slides.com