Failure and success of the spectral bias prediction

for Laplace Kernel Ridge Regression:

the case of low-dimensional data

@ICML (2022)

Joint work with A. Sclocchi and M. Wyart

The learning algorithm

Regression of a target function \(f^*\) from \(P\) examples \(\{x_i,f^*(x_i)\}_{i=1,...,P}\).

Interest in kernels renewed by lazy neural networks

f_P(x)=\sum_{i=1}^P a_i K(x_i,x)

\text{min}\left[\sum\limits_{i=1}^P\left|f^*(x_i)-f_P(x_i)\right|^2 +\lambda ||f_P||_K^2\right]

Train loss:

\(K(x,y)=e^{-\frac{|x-y|}{\sigma}}\)

E.g. Laplacian Kernel

Kernel Ridge Regression (KRR):

Key object: generalization error \(\varepsilon_t\)
Typically \(\varepsilon_t\sim P^{-\beta}\), \(P\) number of training data

Predicting generalization of KRR

[Canatar et al., Nature (2021)]

General framework for KRR

Predicts that KRR has a spectral bias in its learning:

\(\rightarrow\) KRR learns the first \(P\) eigenmodes of \(K\)

\(\rightarrow\) \(f_P\) is self-averaging with respect to sampling

Obtained by replica theory

Works well on some real data for \(\lambda>0\)

\(\rightarrow\) what is the validity limit?

Our toy model

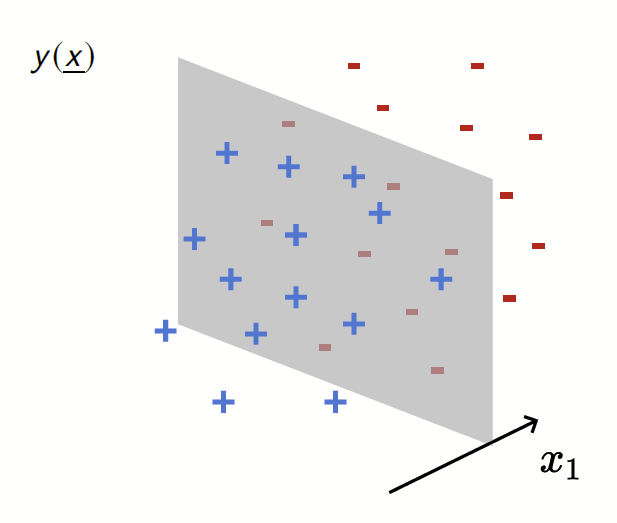
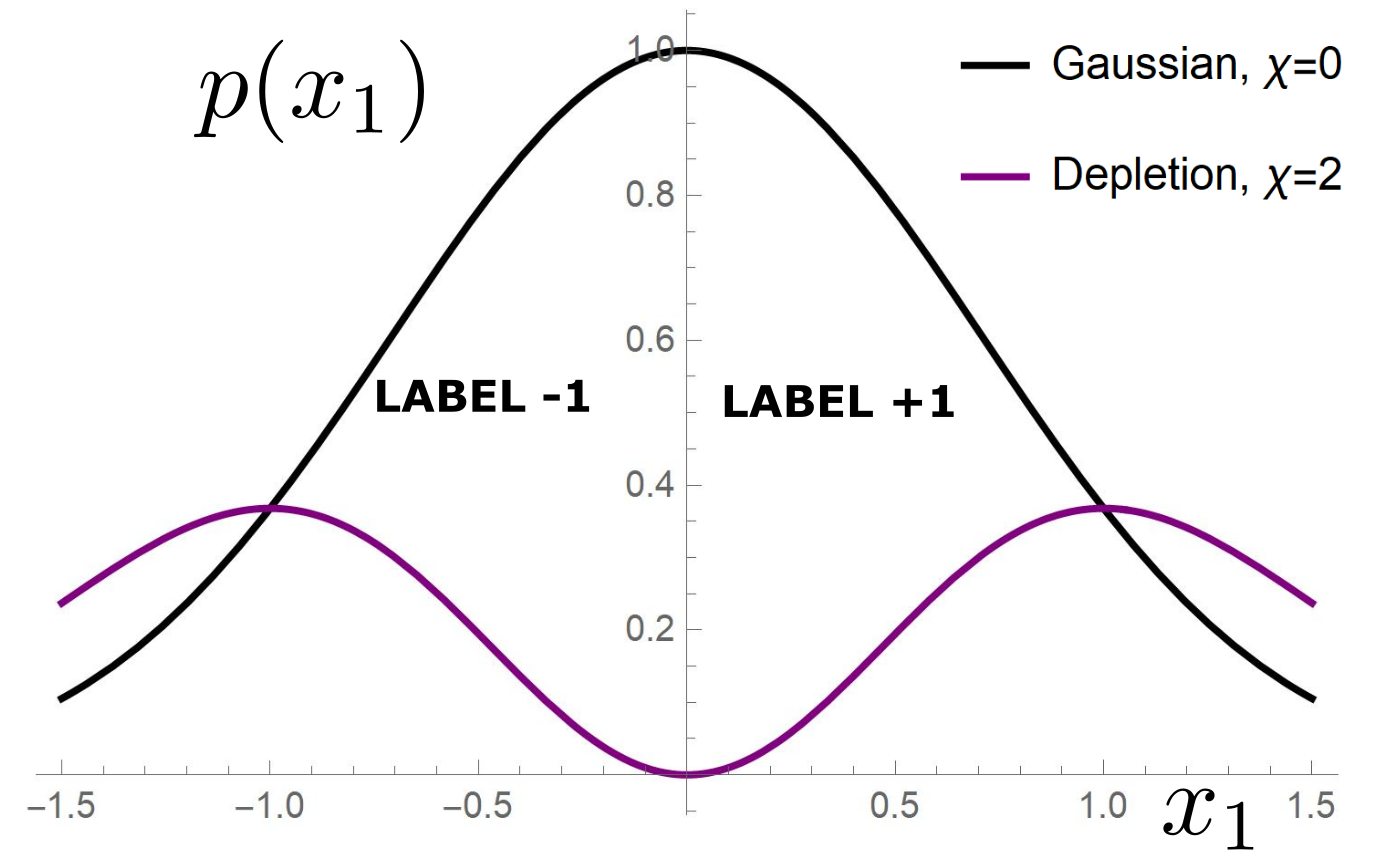
Depletion of points around the interface

p(x_1)= \frac{1}{\mathcal{Z}}\color{red}{|x_1|^\chi}\color{black} e^{-x_1^2}

Data: \(x\in\mathbb{R}^d\)

Label: \(f^*(x_1,x_{\bot})=\text{sign}[x_1]\)

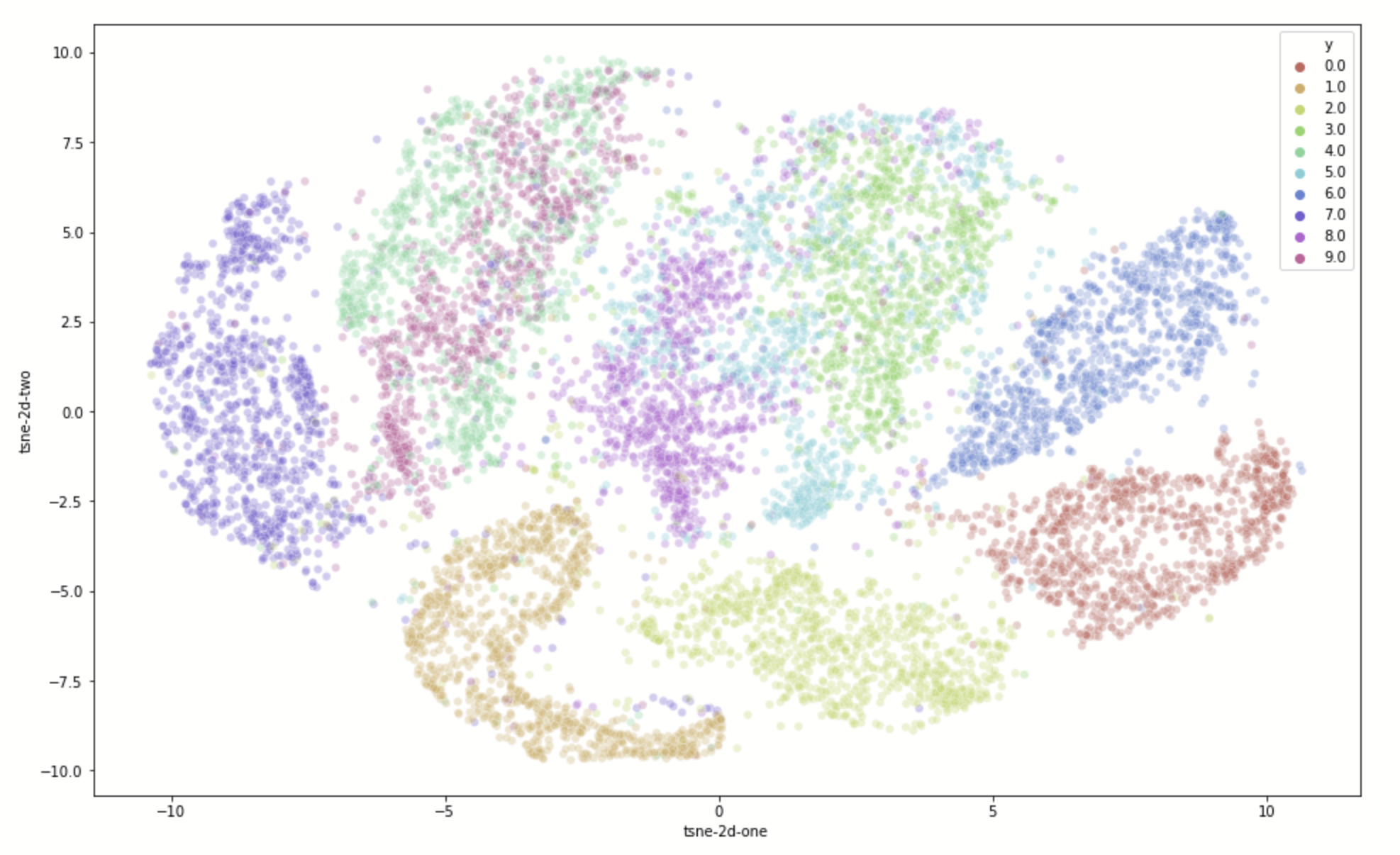
Motivation:

evidence for gaps between clusters in datasets like MNIST

Predictor in the toy model

(1) Spectral bias predicts a self-averaging predictor controlled by a characteristic length \( \ell(\lambda,P) \propto \lambda/P \)

For fixed regularizer \(\lambda/P\):

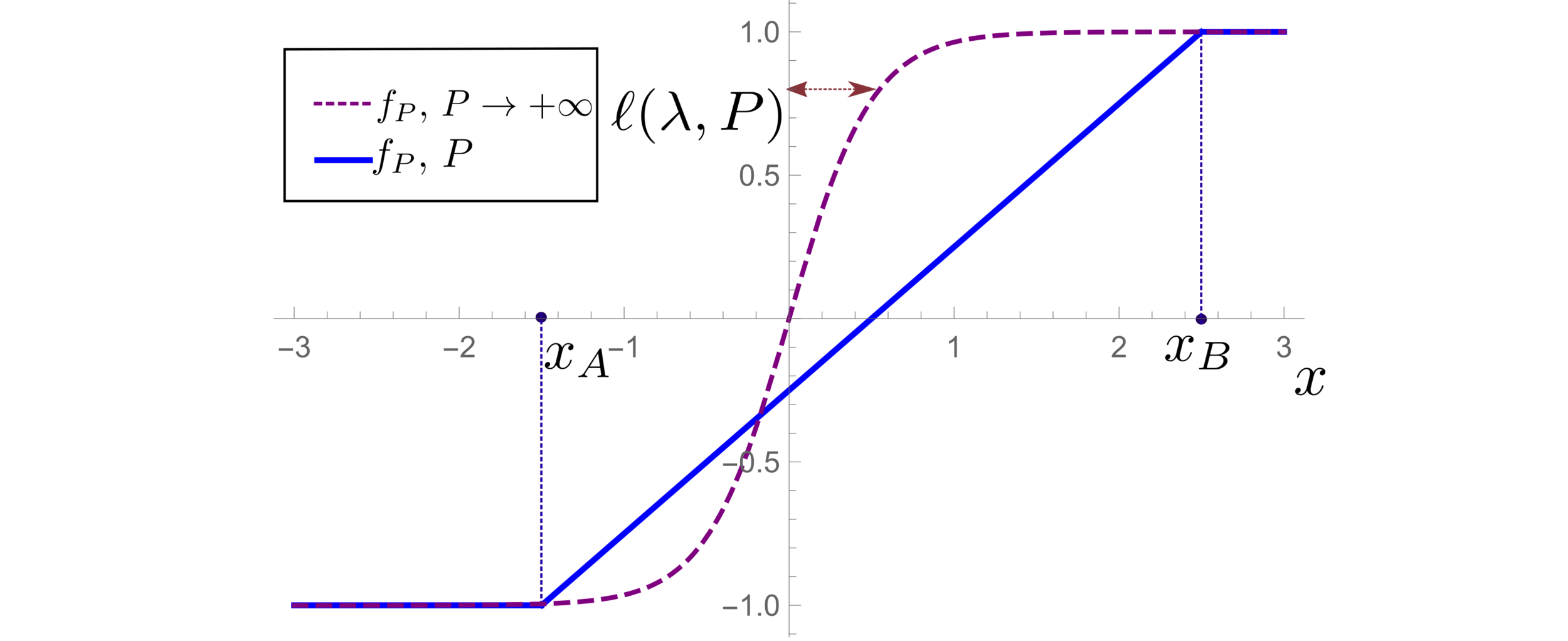
(2) When the number of sampling points \(P\) is not enough to probe \( \ell(\lambda,P) \):

\(f_P\) is controlled by the statistics of the extremal points \(x_{\{A,B\}}\)
spectral bias breaks down.

\(d=1\)

\varepsilon_B \sim P^{-(1+\frac{1}{d})\frac{1+\chi}{1+d+\chi}}

\varepsilon_t \sim P^{-\frac{1+\chi}{d+\chi}}

\neq

Different predictions for

\(\lambda\rightarrow0^+\)

For \(\chi=0\): equal
For \(\chi>0\): equal for \(d\rightarrow\infty\)

\lambda^*_{d,\chi}\sim P^{-\frac{1}{d+\chi}}

Crossover at:

\(\lambda\)

Spectral bias failure

Spectral bias success

Conclusions

For small ridge: correct just for \(d\rightarrow\infty\).

Thank you for your attention!

For which kind of data spectral bias fails?

Depletion of points close to decision boundary

Still missing a comprehensive theory for

KRR test error for vanishing regularization

BACKUP SLIDES

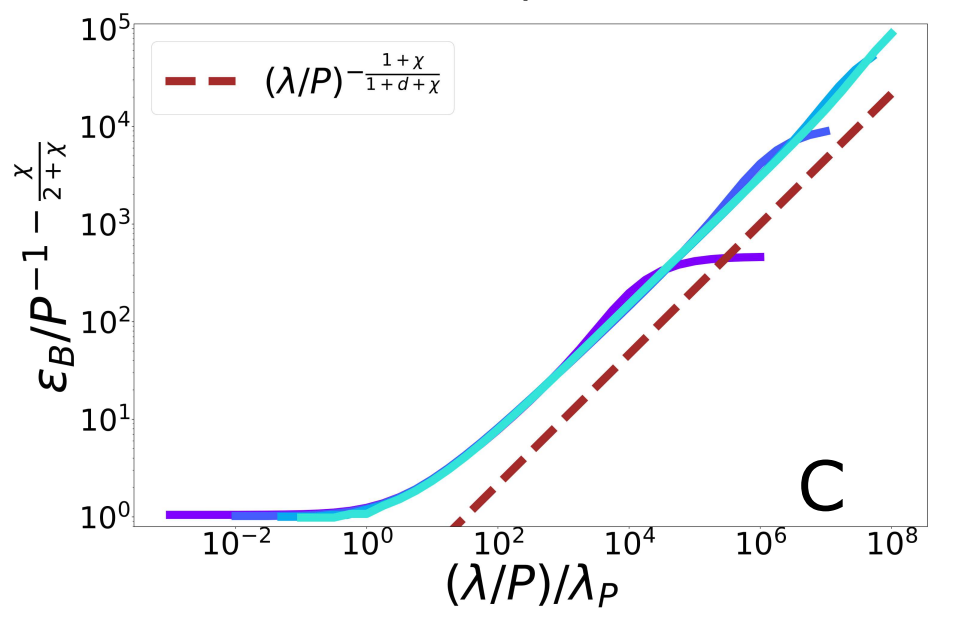
Scaling Spectral Bias prediction

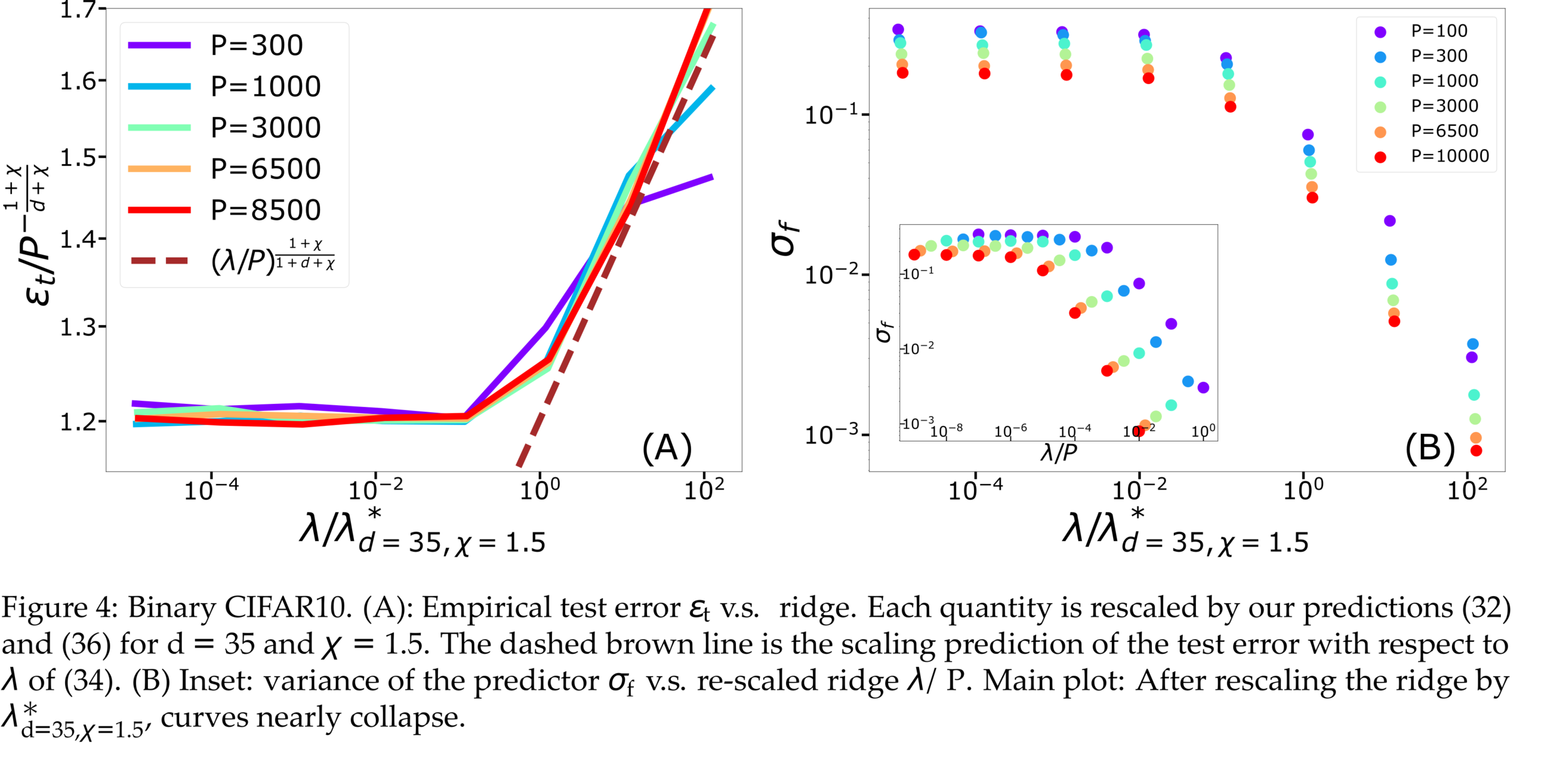
Fitting CIFAR10

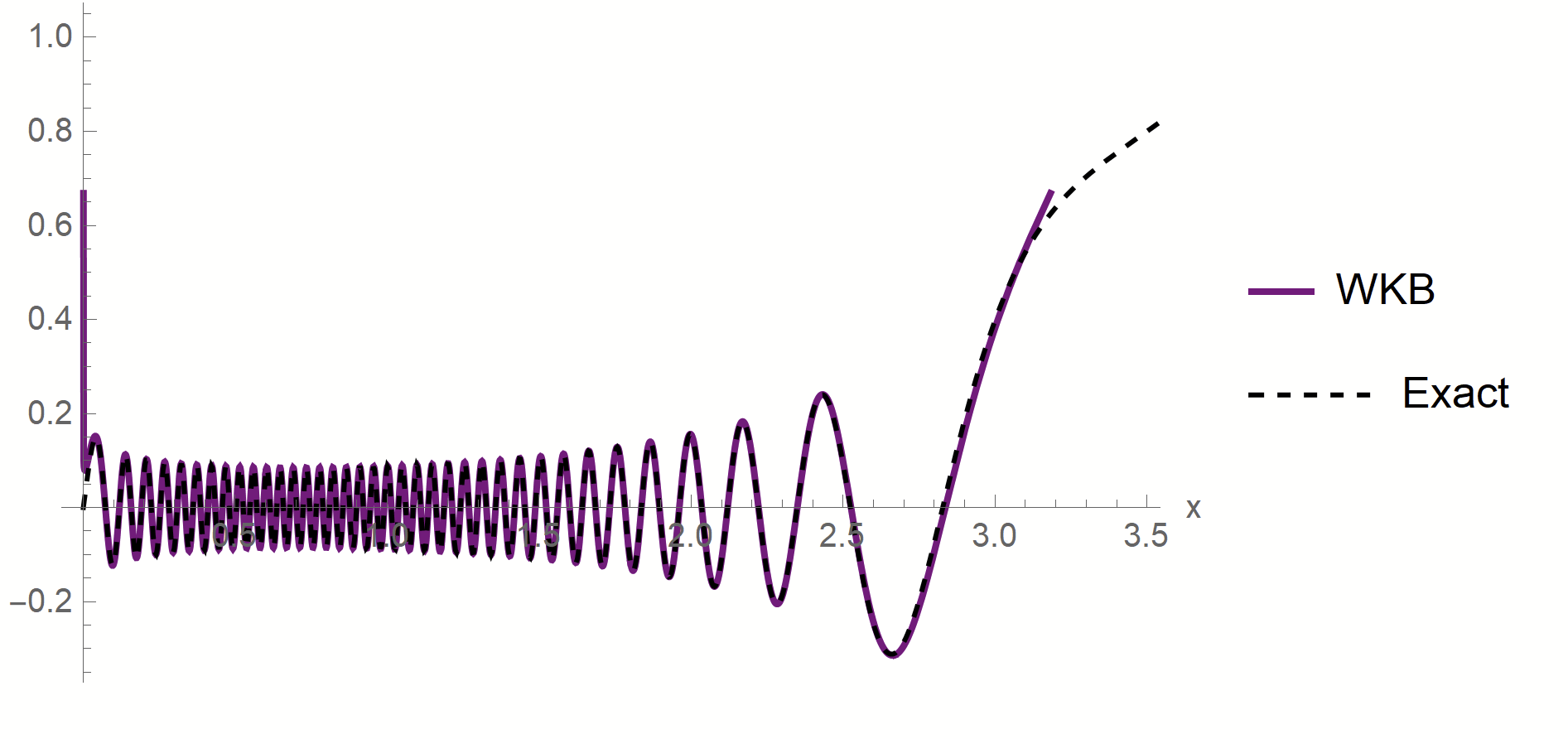
Proof:

WKB approximation of \(\phi_\rho\) in [\(x_1^*,\,x_2^*\)]:

\(\phi_\rho(x)\sim \frac{1}{p(x)^{1/4}}\left[\alpha\sin\left(\frac{1}{\sqrt{\lambda_\rho}}\int^{x}p^{1/2}(z)dx\right)+\beta \cos\left(\frac{1}{\sqrt{\lambda_\rho}}\int^{x}p^{1/2}(z)dx\right)\right]\)

x_1^*

x_2^*

MAF approximation outside [\(x_1^*,\,x_2^*\)]

\(x_1*\sim \lambda_\rho^{\frac{1}{\chi+2}}\)

\(x_2*\sim (-\log\lambda_\rho)^{1/2}\)

WKB contribution to \(c_\rho\) is dominant in \(\lambda_\rho\)
Main source WKB contribution:

first oscillations

Formal proof:

Take training points \(x_1<...<x_P\)
Find the predictor in \([x_i,x_{i+1}]\)
Estimate contribute \(\varepsilon_i\) to \(\varepsilon_t\)
Sum all the \(\varepsilon_i\)

Characteristic scale of predictor \(f_P\), \(d=1\)

\sigma^2 \partial_x^2 f_P(x) =\left(\frac{\sigma}{\lambda/P}p(x)+1\right)f_P(x)-\frac{\sigma}{\lambda/P}p(x)f^*(x)

Minimizing the train loss for \(P \rightarrow \infty\):

\(\rightarrow\) A non-homogeneous Schroedinger-like differential equation

\(\rightarrow\) Its solution yields:

\ell(\lambda,P)\sim \left(\frac{\lambda\sigma}{P}\right)^{\frac{1}{(2+\chi)}}

Characteristic scale of predictor \(f_P\), \(d>1\)

Let's consider the predictor \(f_P\) minimizing the train loss for \(P \rightarrow \infty\).

f_P(x)=\int d^d\eta \frac{p(\eta) f^*(\eta)}{\lambda/P} G(x,\eta)

With the Green function \(G\) satisfying:

\int d^dy K^{-1}(x-y) G_{\eta}(y) = \frac{p(x)}{\lambda/P} G_{\eta}(x) + \delta(x-\eta)

In Fourier space:

\mathcal{F}[K](q)^{-1} \mathcal{F}[G_{\eta}](q) = \frac{1}{\lambda/P} \mathcal{F}[p\ G_{\eta}](q) + e^{-i q \eta}

In Fourier space:

\mathcal{F}[K](q)^{-1} \mathcal{F}[G_{\eta}](q) = \frac{1}{\lambda/P} \mathcal{F}[p\ G_{\eta}](q) + e^{-i q \eta}

\begin{aligned} \mathcal{F}[G](q)&\sim q^{-1-d}\ \ \ \text{for}\ \ \ q\gg q_c\\ \mathcal{F}[G](q)&\sim \frac{\lambda}{P}q^\chi\ \ \ \text{for}\ \ \ q\ll q_c\\ \text{with}\ \ \ q_C&\sim \left(\frac{\lambda}{P}\right)^{-\frac{1}{1+d+\chi}} \end{aligned}

Two regimes:

\(G_\eta(x)\) has a scale:

\ell(\lambda,P)\sim 1/q_c\sim \left(\frac{\lambda}{P}\right)^{\frac{1}{1+d+\chi}}