Failure and success of the spectral bias prediction

for Kernel Ridge Regression:

the case of low-dimensional data

Supervised Machine Learning (ML)

Used to learn a rule from data.
Learn from \(P\) examples \(\{x_i,y_i\}\) a rule \(f_P(x)\).

Key object: generalization error \(\varepsilon_t\) on new data
Typically \(\varepsilon_t\sim P^{-\beta}\)

General high-dimensional arguments: very small \(\beta\sim 1/d\)

In practice: very good performance

ML is able to capture structure of data

How \(\beta\) depends on data structure, the task and the ML architecture?

Curse of Dimensionality

\(\varepsilon_t\sim P^{-\beta}\)

A bridge with Kernel Methods

Neural networks with infinite width, specific initialization

\(\varepsilon_t\) equivalence

[Jacot et al. 2018]

Kernel methods

Kernel Methods: a brief overview

Predictor \(f_P\) linear in non-linear \(K\):

f_P(x)=\sum_{i=1}^P a_i K(x_i,x)

Pros:

Coefficients \(a_i\) found with a convex minimisation problem
Choose the kernel \(K\)

Cons:

1. High computational cost

Kernel Ridge Regression (KRR)

\text{min}\left[\sum\limits_{i=1}^P\left|f^*(x_i)-f_P(x_i)\right|^2 +\lambda ||f_P||_K^2\right]

\varepsilon_t = \int\,dx\, p(x) (f_P(x)-f^*(x))^2

True function: \(f^*(x)\)

Data: \(x\sim p(x)\)

Train loss:

Test error:

Can we apply KRR

on realistic toy models of data?

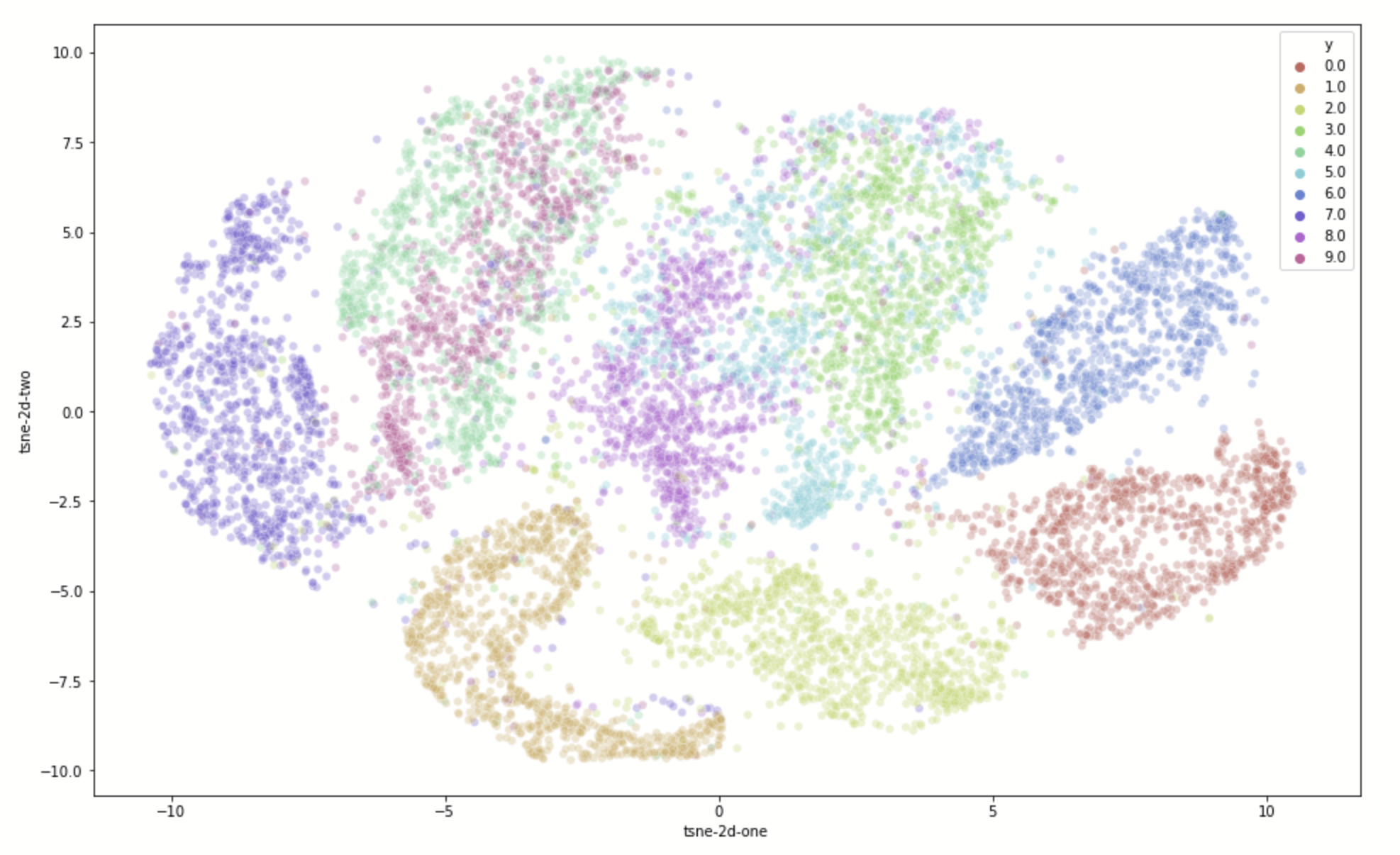
MNIST
Reducing dimensions for visualization (t-SNE)
From towardsdatascience.com
From 28x28 dimensions to 2, with \(10^5\) samples

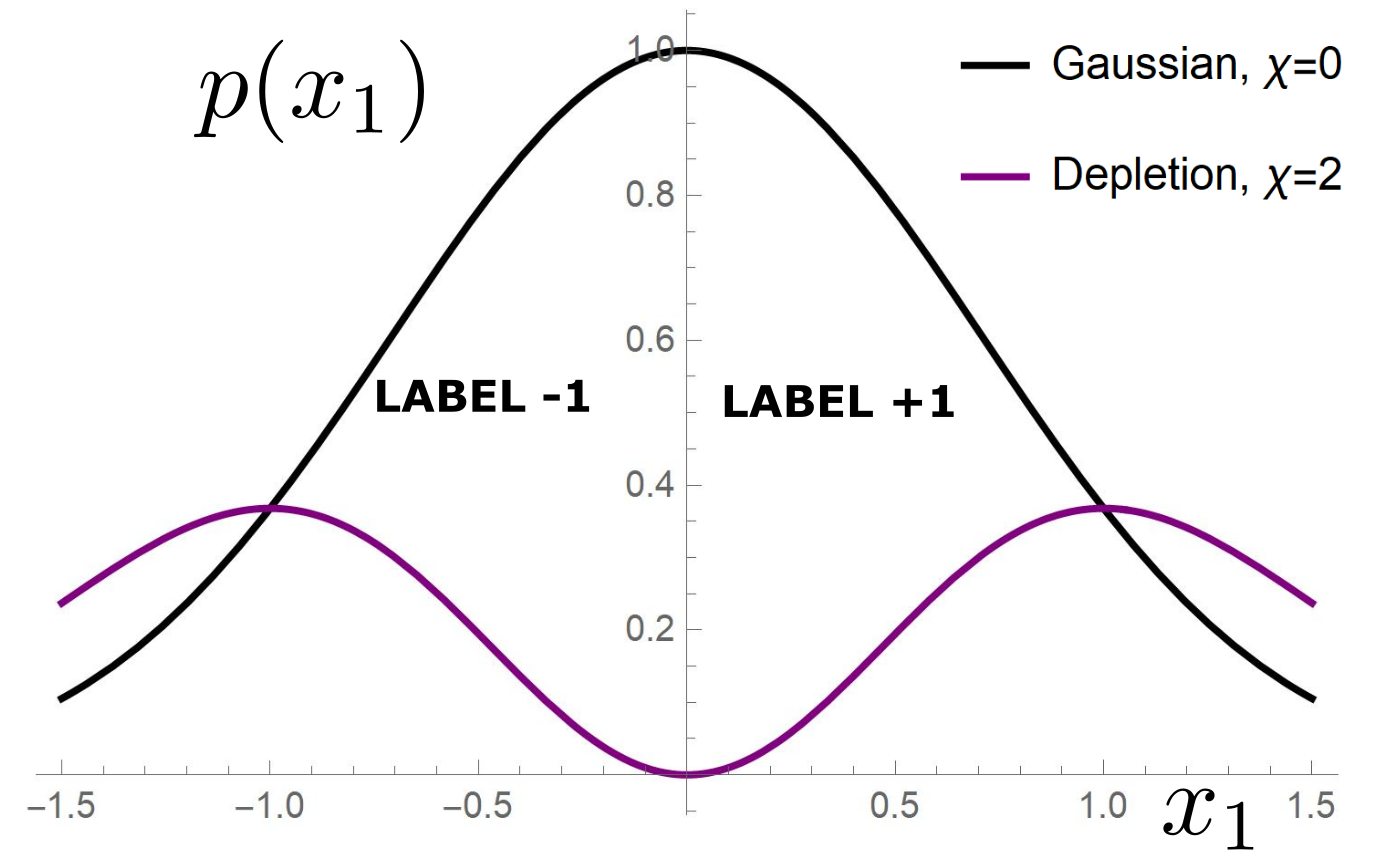
Depleted Stripe Model

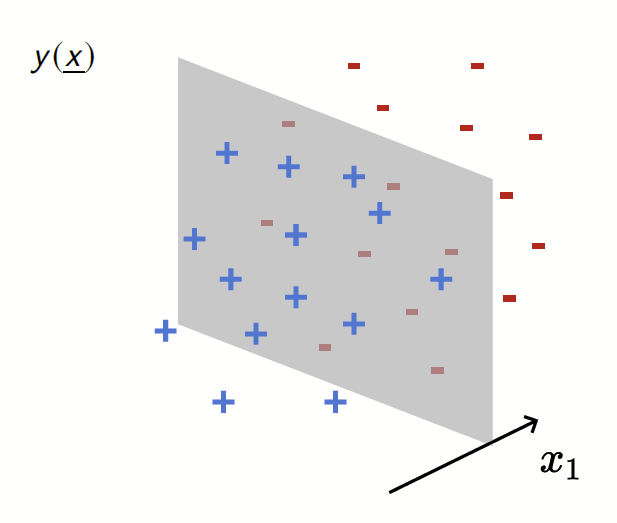
[Paccolat, Spigler, Wyart 2020]

Data: isotropic Gaussian

Label: \(f^*(x_1,x_{\bot})=\text{sign}[x_1]\)

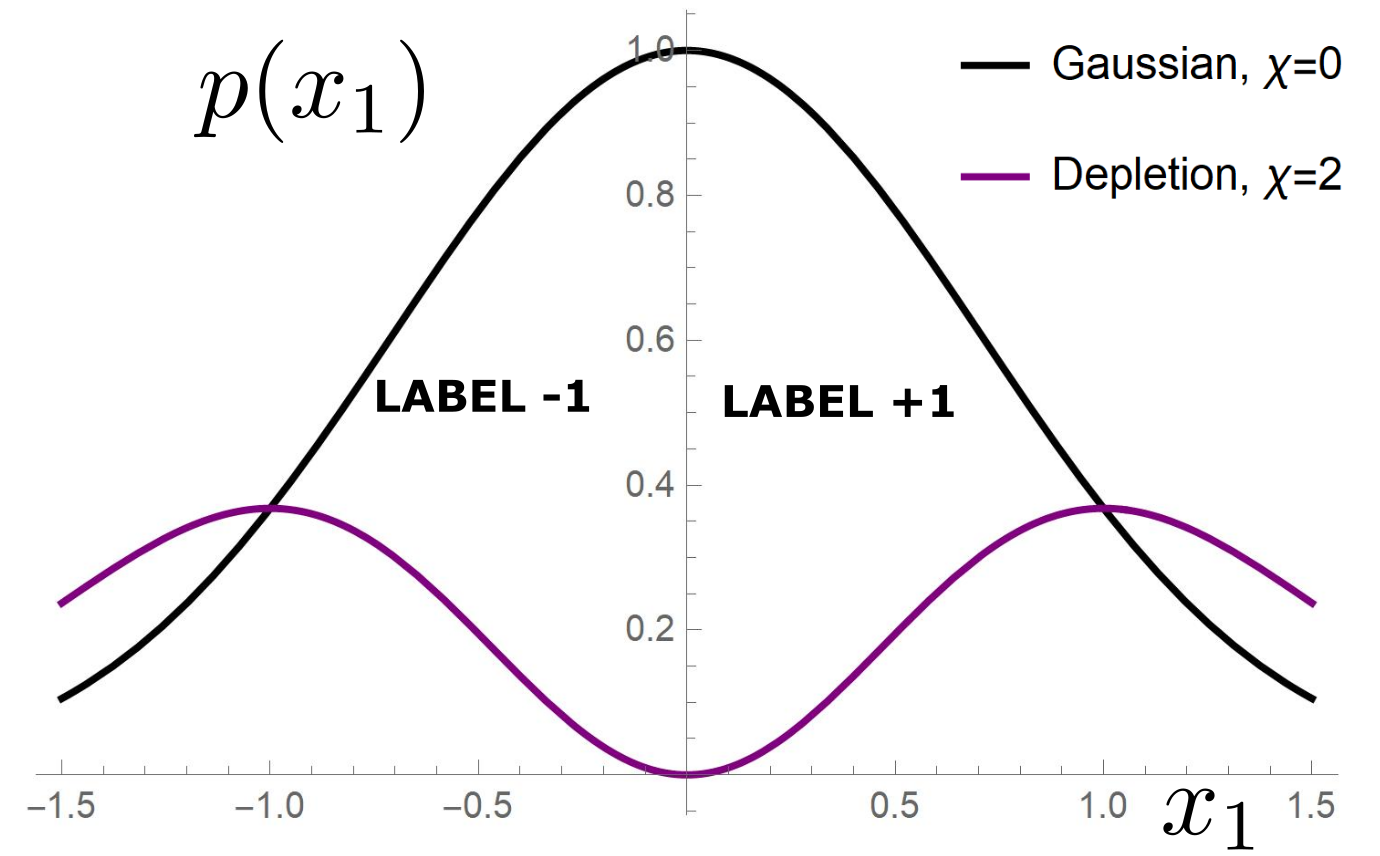
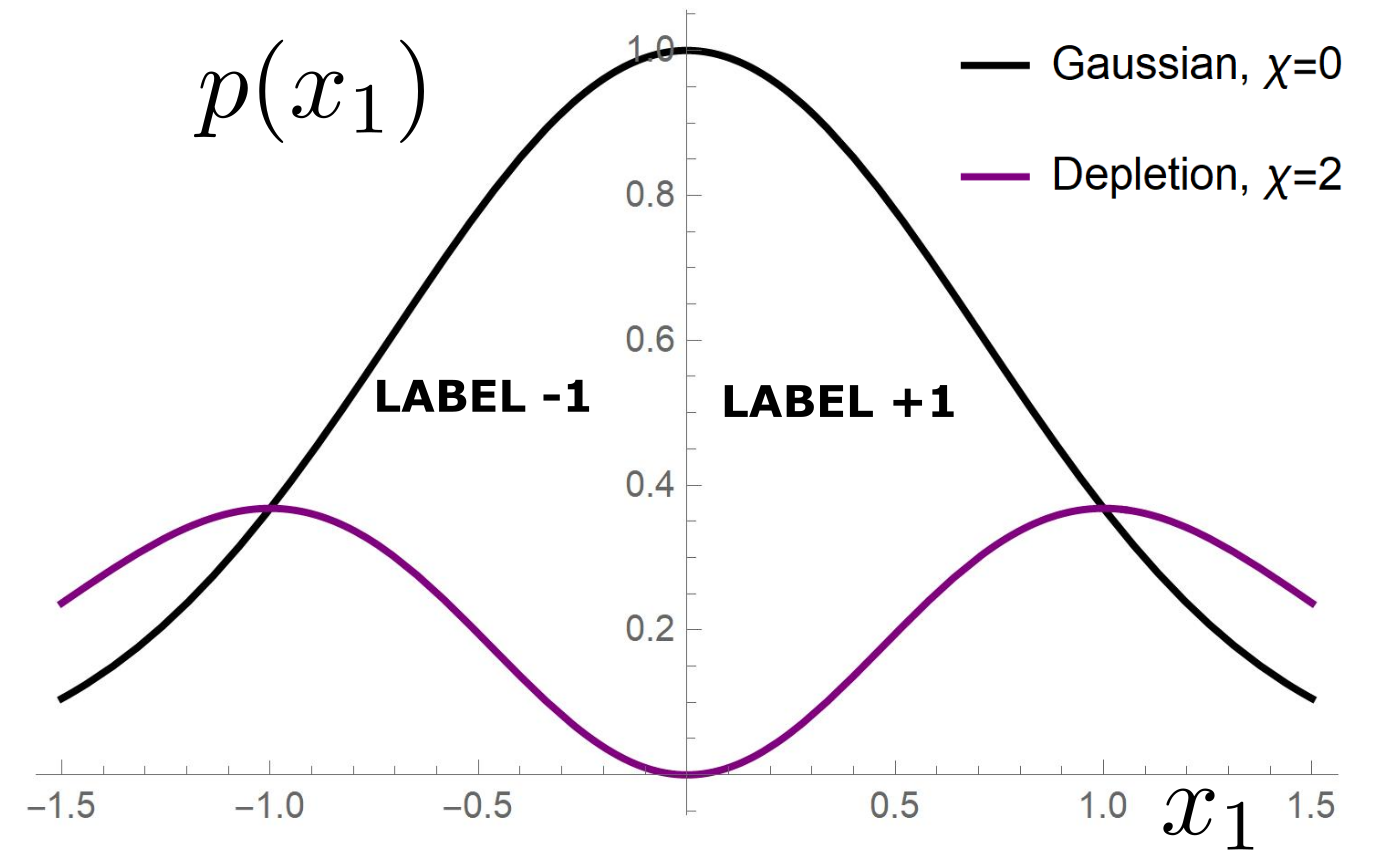
Depletion of points around the interface

p(x_1)= \frac{1}{\mathcal{Z}}|x_1|^\chi e^{-x_1^2}

[Tomasini, Sclocchi, Wyart 2022]

Simple models: testing the KRR literature theories

They work very well on real data
Yet, their validity limit is not clear
Which are the real data features which allow their success?

Deeper understanding with simple models

General framework for regression

[Bordelon et al. 2020] [Canatar et al. 2020] [Loureiro et al. 2021]

Relies on eigendecomposition of \(K\):

\int p(y) K(y,x)\phi_{\rho}(y)dy = \lambda_\rho\phi_{\rho}(x)

Eigenvectors \(\{\phi_{\rho}\}\) and eigenvalues \(\{\lambda_{\rho}\}\)

f^*(x)=\sum\limits_{\rho=1}^{\infty} c_{\rho}\phi_{\rho}(x)

\varepsilon_B \approx \sum\limits_{\rho>P}c^2_{\rho}

\( 2b>(a-1)\)

Noiseless setting
Ridgeless limit \(\lambda\rightarrow0^+\)

\lambda_\rho\sim \rho^{-b}

c_\rho\sim \rho^{-a}

Replica calculation + Gaussian approximation

Spectral Bias:

KRR first learns the \(P\) modes with largest \(\lambda_\rho\)

What happens in our context?

\(f^*(x_1)=\text{sign}(x_1)\)

p(x_1)= \frac{1}{\mathcal{Z}}|x_1|^\chi e^{-x_1^2}

\(K(x,y)=e^{-\frac{|x-y|}{\sigma}}\)

Rigorous approach for \(d=1\)
Scaling arguments for \(d>1\)

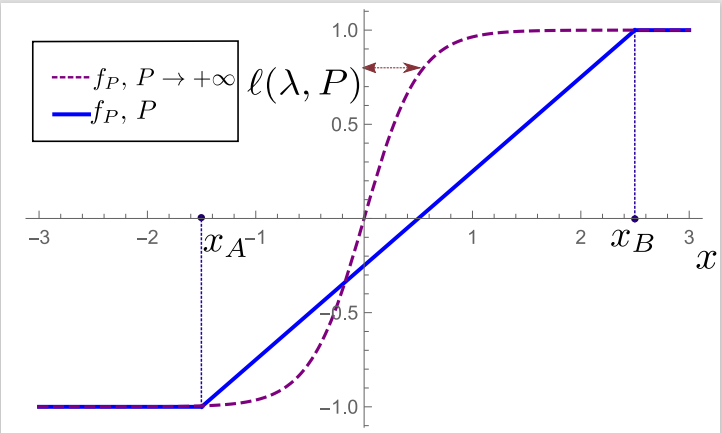
A physical intuition

\ell(\lambda,P) \propto \lambda/P

For fixed \(\lambda/P\):

Test error for \(\lambda\rightarrow0^+\):

what do we expect?

The predictor \(f_P\) is governed by two extremal points in the sample

\(x_A\) and \(x_{B}\)

\(\varepsilon_t \sim \int_0^{x_B}x^\chi dx \sim P^{-1}\)

For \(\lambda\rightarrow0^+\) and large \(P\)

\(\varepsilon_t\sim P^{-1}\) for \(\forall \chi\ge0\)

Eigenvectors \( \phi_{\rho} \) satisfy the following Schroedinger-like differential equation (ODE):

\phi_{\rho}^{''}(x)=\frac{1}{\lambda_{\rho}}\left(-2\frac{p(x)}{\sigma} +\frac{\lambda_{\rho} }{\sigma^2}\right)\phi_{\rho}(x)

Spectral Bias prediction: eigendecomposition

\phi_{\rho}^{''}(x)=\frac{2m}{\hbar^2}\left( V(x)-E\right)\phi_{\rho}(x)

Solve the ODE, via Wentzel–Kramers–Brillouin (WKB):

\(\phi_\rho(x)\sim \frac{1}{p(x)^{1/4}}\sin\left(\frac{1}{\sqrt{\lambda_\rho}}\int^{x}p^{1/2}(z)dx\right)\)

Compute \(|c_\rho|=\int_{-\infty}^{\infty}f^*(x)\phi_\rho(x)p(x)dx\) at leading order in \(\lambda_\rho\).

\(|c_{\rho}|\sim \lambda_\rho^{\frac{\frac{3}{4}\chi+1}{\chi+2}}\)

Getting the coefficients \(c_\rho \)

for small \(\lambda_\rho\)

Spectral bias prediction

\(\lambda_\rho\sim\rho^{-2}\)

\(\varepsilon_B\approx \sum\limits_{\rho>P}c^2_{\rho}\approx P^{-1-\frac{\chi}{\chi+2}} \)

From the boundary condition \(|\phi(x)|\rightarrow 0\) for \(|x|\rightarrow \infty\)

Different predictions:

\(\varepsilon_B\sim P^{-1-\frac{\chi}{\chi+2}}\neq \varepsilon_t \sim P^{-1}\)

\varepsilon/P^{-1}

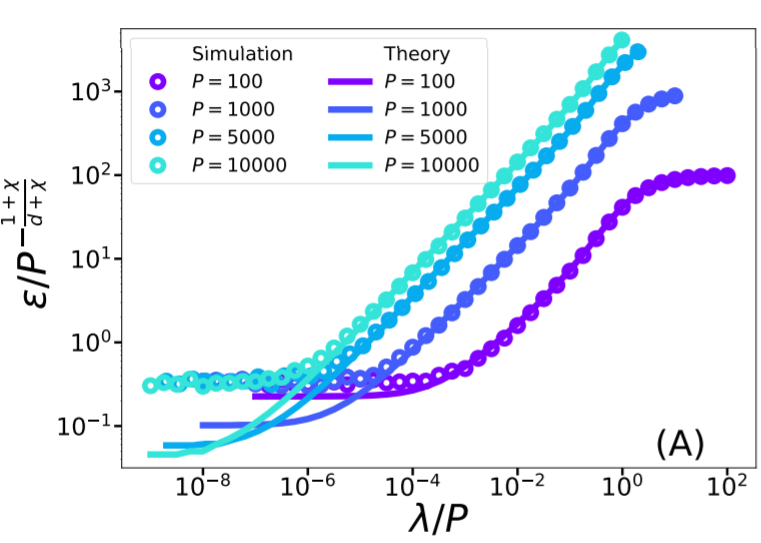
\(d=1\)

\(\chi=1\)

What happens for larger \(\lambda\)?

\varepsilon/P^{-1}

Increasing \(\lambda/P\) \(\rightarrow\) Increasing \(\ell(\lambda,P)\)

\(\rightarrow\) The predictor \(f_P\) is controlled by \(\ell(\lambda,P)\) even for small \(P\)

\(\rightarrow\) The predictor \(f_P\) is self-averaging

What happens for larger \(\lambda\)?

The self-averageness crossover

Characteristic length of \(f_P\) for \(P\rightarrow \infty\) and \(\frac{\lambda}{P}\) fixed (\( \ell(\lambda,P)\) wins):

\( \ell(\lambda,P) \sim \left(\frac{ \lambda \sigma}{P}\right)^{\frac{1}{2+\chi}}\)

Characteristic length of \(f_P\) for \(\lambda\rightarrow 0^+\) (\( x_B\) wins):

\(x_B\sim P^{-\frac{1}{\chi+1}}\)

\(\rightarrow\) Crossover:

\lambda^*_{1,\chi}\sim P^{-\frac{1}{1+\chi}}

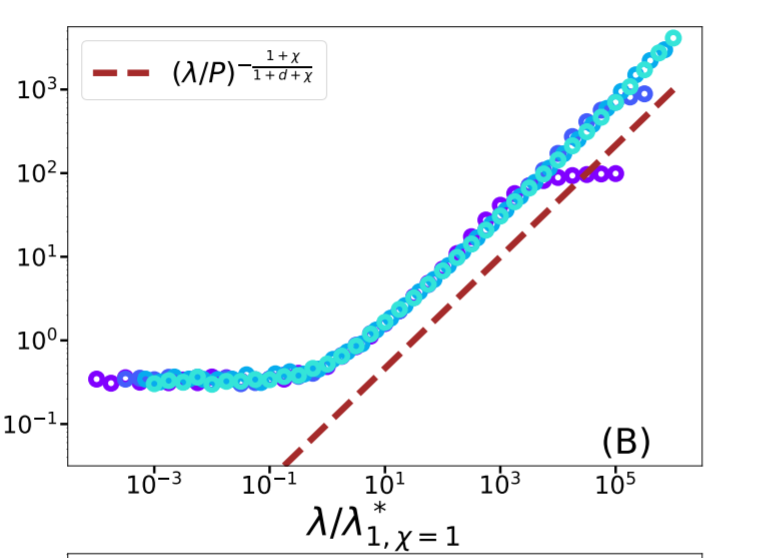
Self-averageness crossover

\varepsilon/P^{-1}

\sigma_f = \langle [f_{P,1}(x_i) - f_{P,2}(x_i)]^2 \rangle

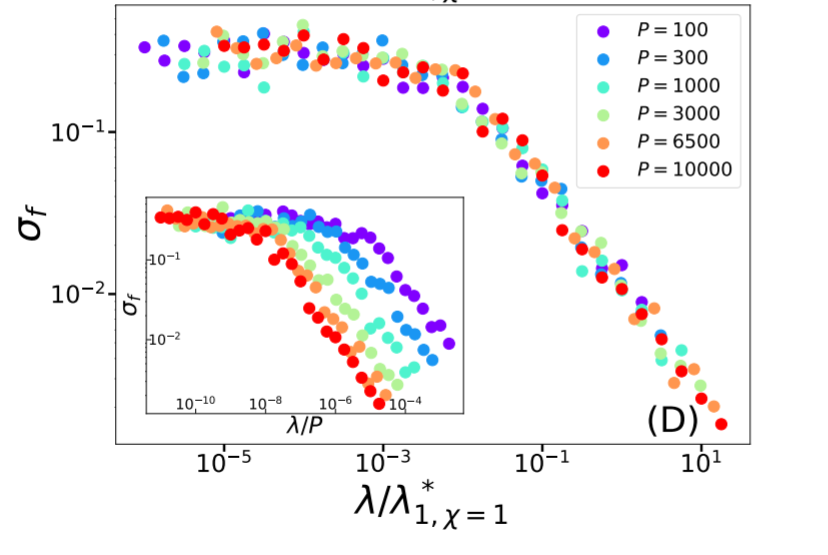
Higher dimension setting:

Test Error

Ridgeless:
- \(f_P\) fluctuates on a distance \(r_\text{min}\sim P^{-1/(d+\chi)}\)

\varepsilon_t \sim\int_0^{r_{min}}dx_1 \, x_1^{\chi}\sim r_{min}^{1+\chi} \sim P^{-\frac{1+\chi}{d+\chi}}

Finite ridge:

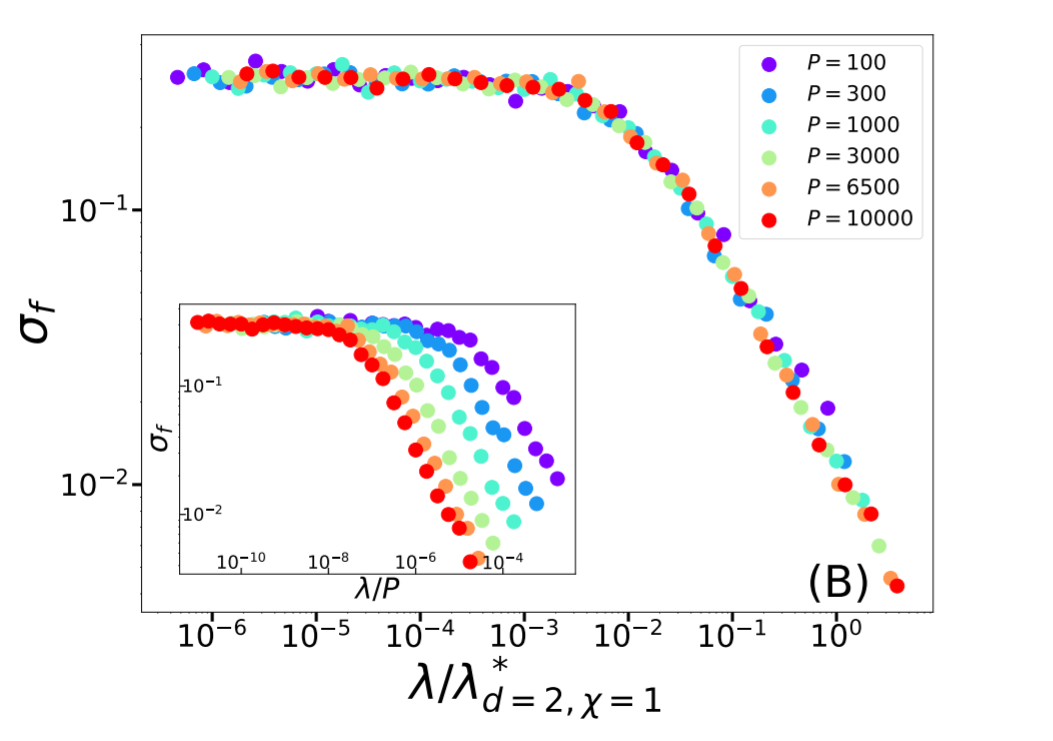
\varepsilon_B \sim \ell(\lambda,P)^{1+\chi} \sim \left(\frac{\lambda}{P}\right)^\frac{1+\chi}{1+d+\chi}

Self-averageness crossover, \(d>1\)

Comparing \(r_\text{min}\) and \(\ell(\lambda,P)\):

\(\lambda^*_{d,\chi}\sim P^{-\frac{1}{d+\chi}}\)

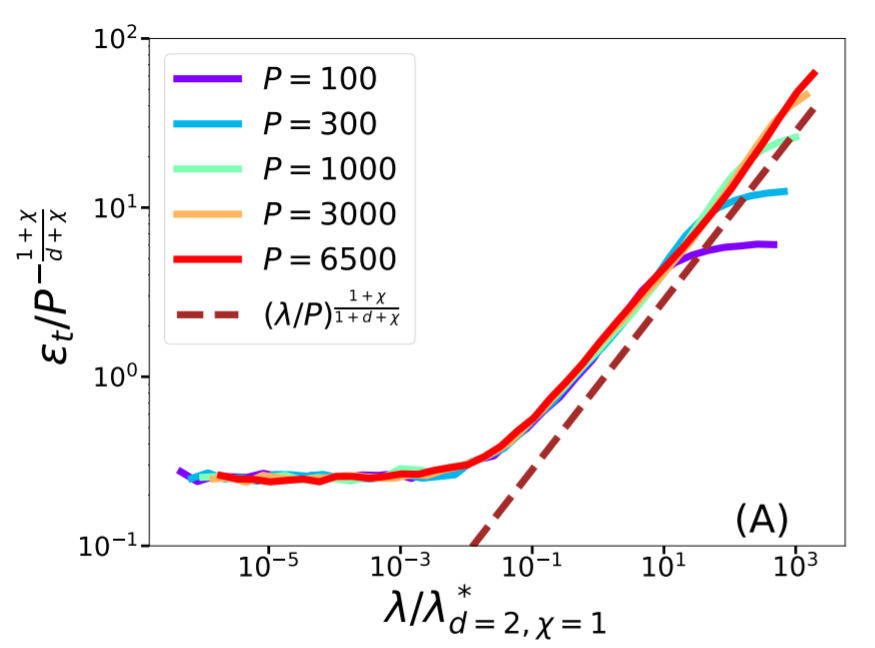
Higher dimension setting:

Test Error (ridgeless)

\varepsilon_B \sim \left(\frac{\lambda_P}{P}\right)^\frac{1+\chi}{1+d+\chi}\sim P^{-(1+\frac{1}{d})\frac{1+\chi}{1+d+\chi}}

\varepsilon_t \sim P^{-\frac{1+\chi}{d+\chi}}

For \(\chi=0\): equal
For \(\chi>0\): equal for \(d\rightarrow\infty\)

\neq

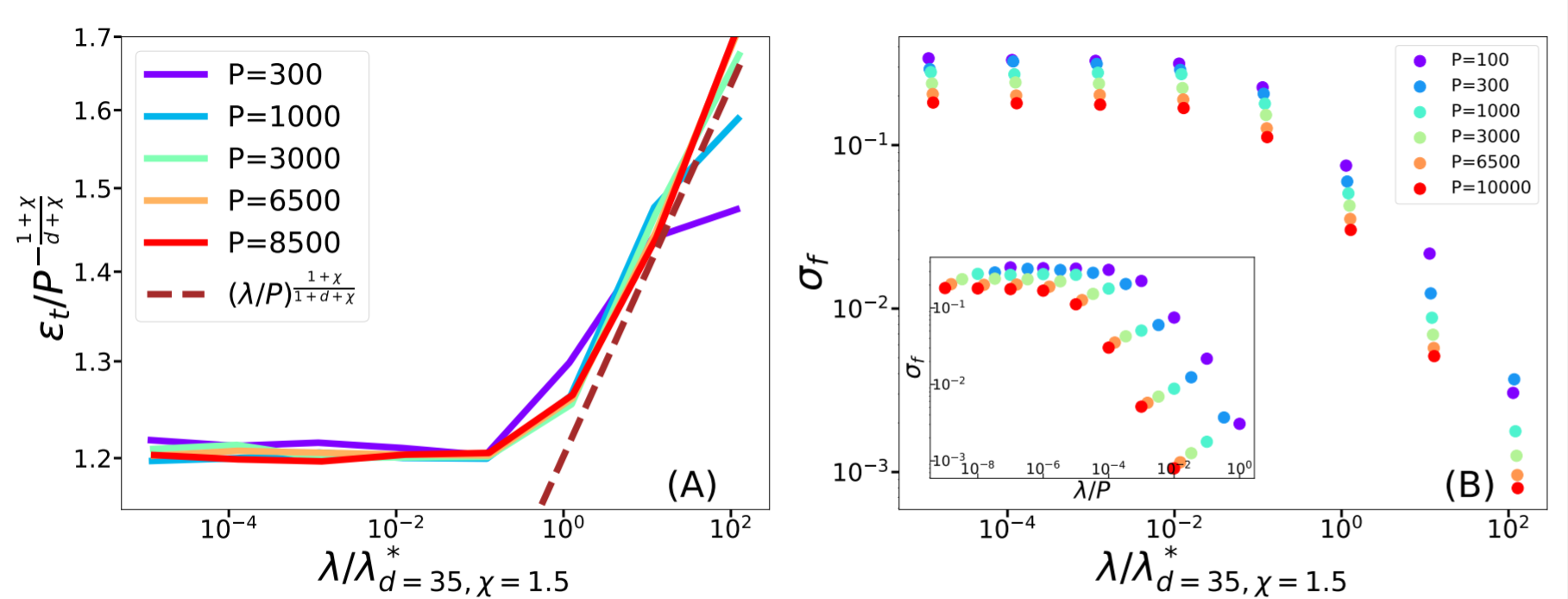
Fitting CIFAR10

Conclusions

Replica/Random Matrix Theory predictions works even for small \(d\), for large ridge.
For small ridge: spectral bias prediction, if \(\chi>0\) correct just for \(d\rightarrow\infty\).

Vanishing density of data points on the boundary: out of Gaussian universality class
\(\phi_\rho(x)\sim \frac{1}{x^{\chi/4}}\):
- \(P(\phi)\sim \phi^{-5-\frac{4}{\chi}}\)
- Eigenvectors not independent: all large for small \(x\)

To note:

Thank you for your attention.

BACKUP SLIDES

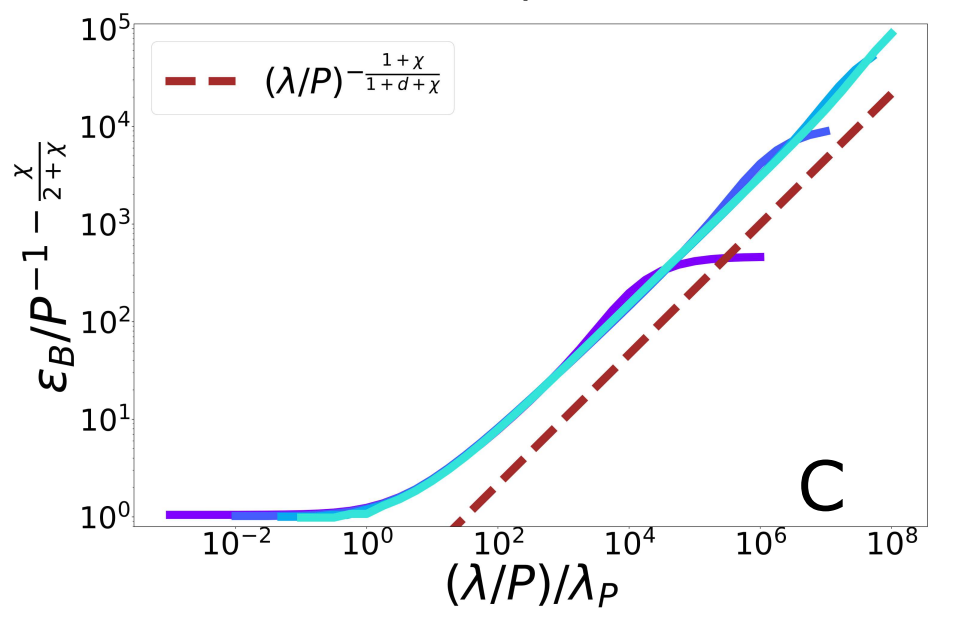
Scaling Spectral Bias prediction

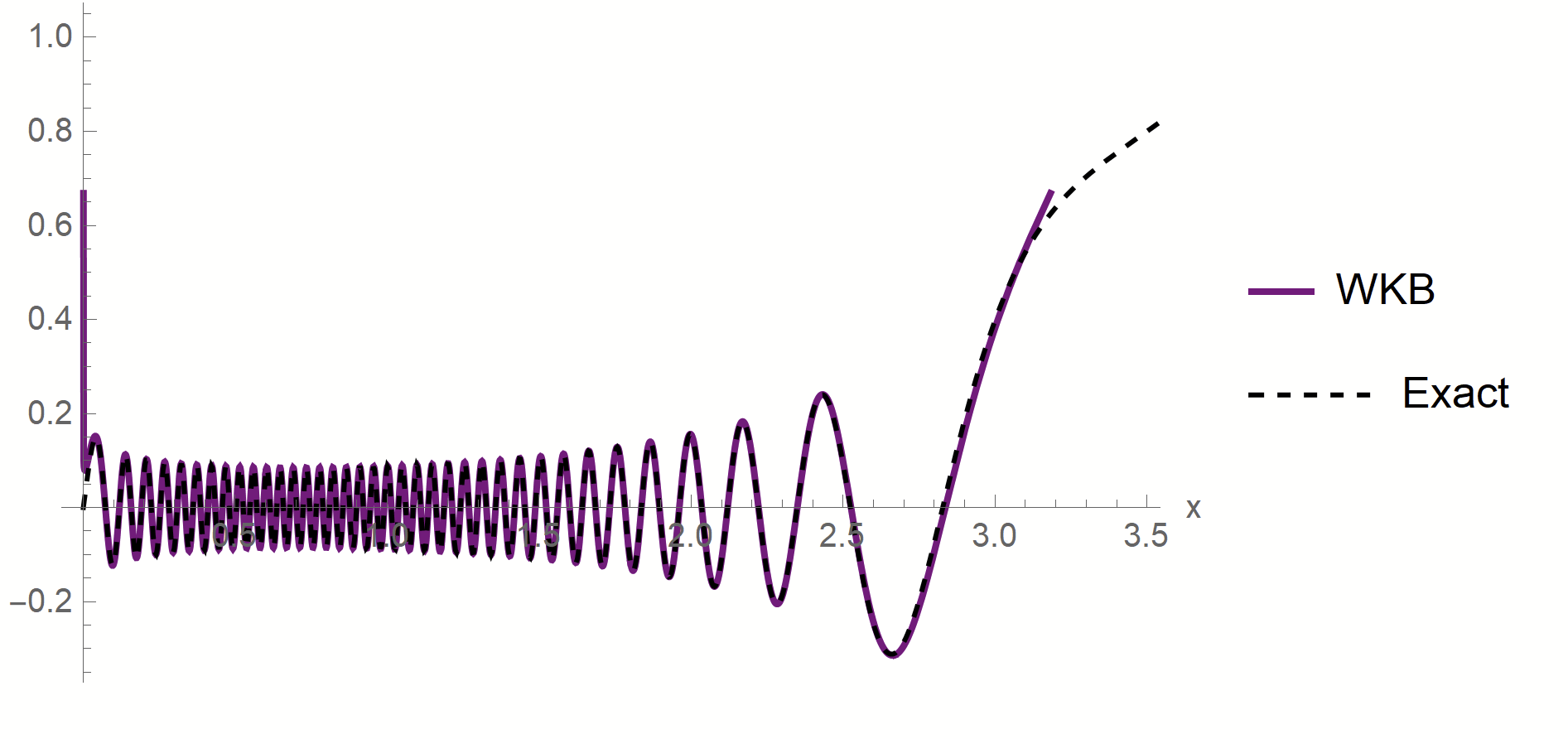
Proof:

WKB approximation of \(\phi_\rho\) in [\(x_1^*,\,x_2^*\)]:

\(\phi_\rho(x)\sim \frac{1}{p(x)^{1/4}}\left[\alpha\sin\left(\frac{1}{\sqrt{\lambda_\rho}}\int^{x}p^{1/2}(z)dx\right)+\beta \cos\left(\frac{1}{\sqrt{\lambda_\rho}}\int^{x}p^{1/2}(z)dx\right)\right]\)

x_1^*

x_2^*

MAF approximation outside [\(x_1^*,\,x_2^*\)]

\(x_1*\sim \lambda_\rho^{\frac{1}{\chi+2}}\)

\(x_2*\sim (-\log\lambda_\rho)^{1/2}\)

WKB contribution to \(c_\rho\) is dominant in \(\lambda_\rho\)
Main source WKB contribution:

first oscillations

Formal proof:

Take training points \(x_1<...<x_P\)
Find the predictor in \([x_i,x_{i+1}]\)
Estimate contribute \(\varepsilon_i\) to \(\varepsilon_t\)
Sum all the \(\varepsilon_i\)

Characteristic scale of predictor \(f_P\), \(d=1\)

\sigma^2 \partial_x^2 f_P(x) =\left(\frac{\sigma}{\lambda/P}p(x)+1\right)f_P(x)-\frac{\sigma}{\lambda/P}p(x)f^*(x)

Minimizing the train loss for \(P \rightarrow \infty\):

\(\rightarrow\) A non-homogeneous Schroedinger-like differential equation

\(\rightarrow\) Its solution yields:

\ell(\lambda,P)\sim \left(\frac{\lambda\sigma}{P}\right)^{\frac{1}{(2+\chi)}}

Characteristic scale of predictor \(f_P\), \(d>1\)

Let's consider the predictor \(f_P\) minimizing the train loss for \(P \rightarrow \infty\).

f_P(x)=\int d^d\eta \frac{p(\eta) f^*(\eta)}{\lambda/P} G(x,\eta)

With the Green function \(G\) satisfying:

\int d^dy K^{-1}(x-y) G_{\eta}(y) = \frac{p(x)}{\lambda/P} G_{\eta}(x) + \delta(x-\eta)

In Fourier space:

\mathcal{F}[K](q)^{-1} \mathcal{F}[G_{\eta}](q) = \frac{1}{\lambda/P} \mathcal{F}[p\ G_{\eta}](q) + e^{-i q \eta}

In Fourier space:

\mathcal{F}[K](q)^{-1} \mathcal{F}[G_{\eta}](q) = \frac{1}{\lambda/P} \mathcal{F}[p\ G_{\eta}](q) + e^{-i q \eta}

\begin{aligned} \mathcal{F}[G](q)&\sim q^{-1-d}\ \ \ \text{for}\ \ \ q\gg q_c\\ \mathcal{F}[G](q)&\sim \frac{\lambda}{P}q^\chi\ \ \ \text{for}\ \ \ q\ll q_c\\ \text{with}\ \ \ q_C&\sim \left(\frac{\lambda}{P}\right)^{-\frac{1}{1+d+\chi}} \end{aligned}

Two regimes:

\(G_\eta(x)\) has a scale:

\ell(\lambda,P)\sim 1/q_c\sim \left(\frac{\lambda}{P}\right)^{\frac{1}{1+d+\chi}}