Large Science Models:

Foundation Models for
Generalizable Insights Into Complex Systems

with Psycho-social Application 

Ishanu Chattopadhyay, PhD

Assistant Professor of Biomedical Informatics & Computer Science

University of Kentucky

DARPA-EA-25-02-05-MAGICS-PA-025

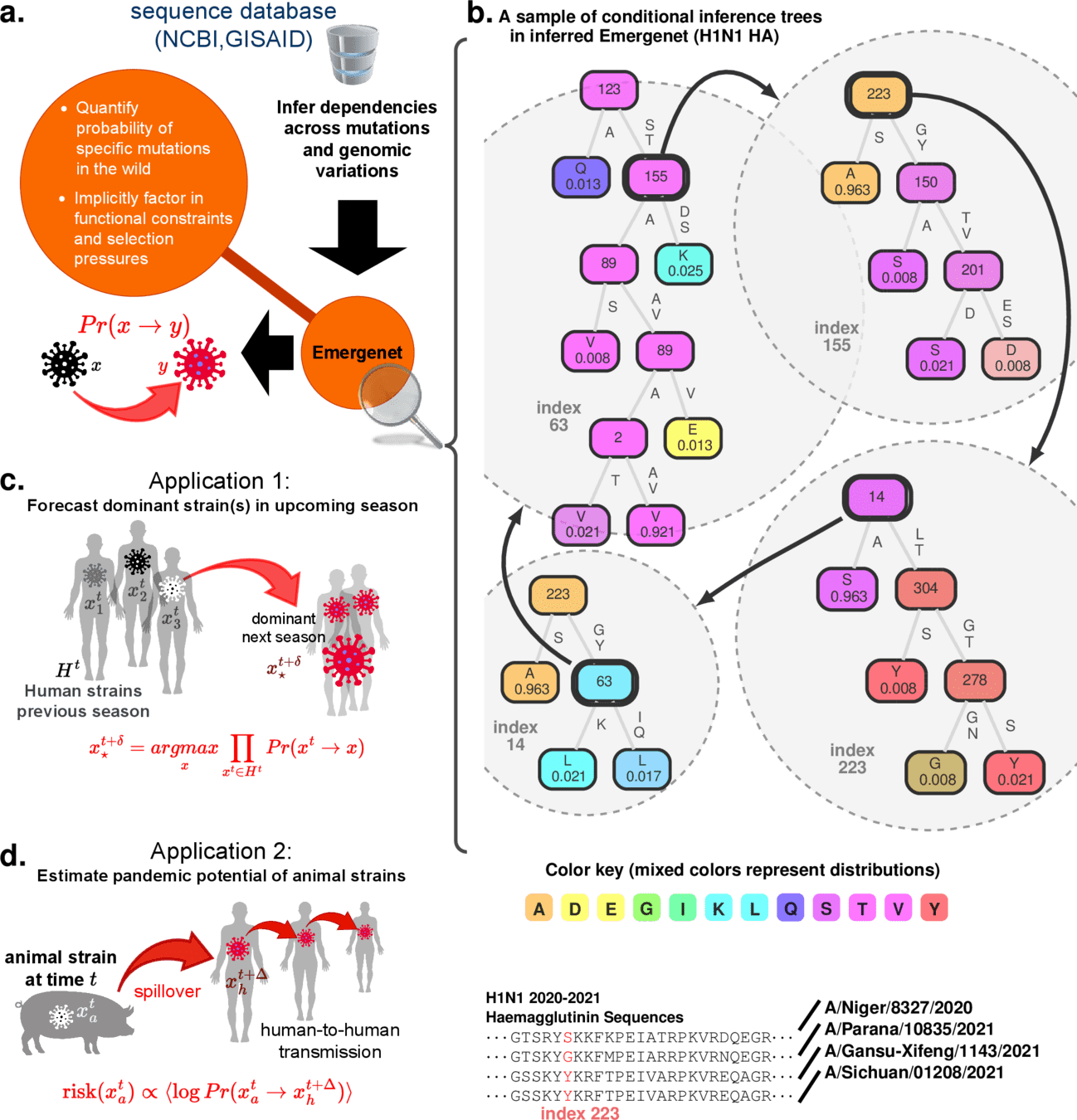
Proposed Concept

  • Develop Foundation models of complex systems with
    • hundreds to thousands of evolving variables with apriori unknown cross-talk
    • no governing equations are know a priori
    • reflexivity: system changes if observed
  • Learn intrinsic system geometry from data
  • Derive  equations of motion with variational principles (stationary action on Lagrangian). 
  • Inference under data sparsity
  • Detect data (in)sufficiency, adapt to model drift
  • Support forward simulation and perturbation analysis
  • Digital twins of individuals & groups wrt to opinion dynamics

MAGICS Alignment

Data inference boundaries & limitations

Alignment validation 

Complex phenomena

Adaptation to model obsolence

Psychosocial domain limitations

Precise validation protocols to assess process drift triggering re-calibration/training

Built-in flexibility for changing contexts and non-ergodicity

Scalable to thousands to millions of variables, intrinsic reflexivity

Validate social theories with granular simulations from  digital twins of opinion dynamics and social behavior

Component LSM predictors enforce statistical significance of splits in recursive partitioning, ensuring precise uncertainty quantification

*Hothorn, Torsten, Kurt Hornik, and Achim Zeileis. "Unbiased recursive partitioning: A conditional inference framework." Journal of Computational and Graphical statistics 15, no. 3 (2006): 651-674.

emergent macro-structure

Component predictor (Conditional Inference Tree*)

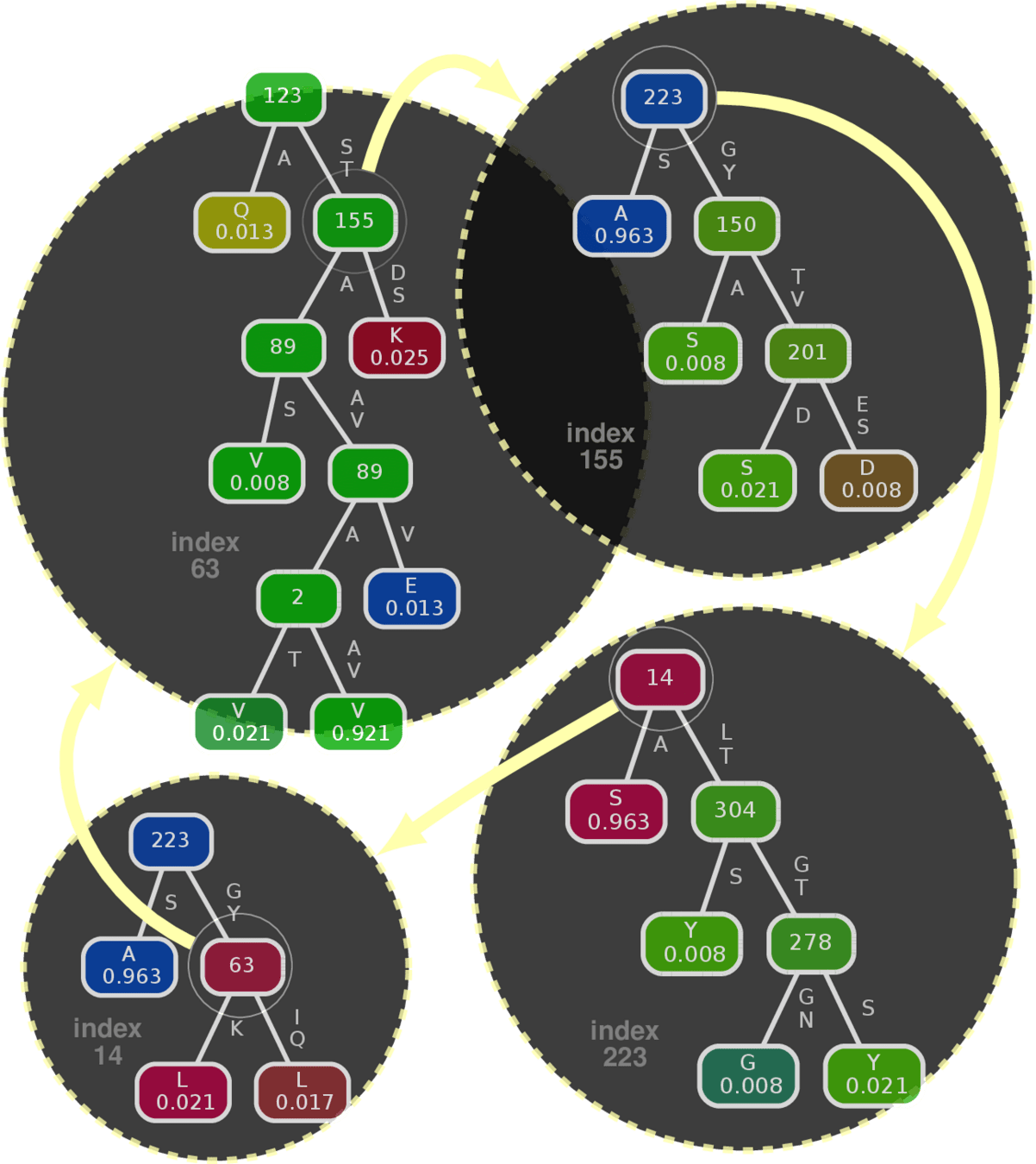
Example: Influenza A HA protein

Recursive

LSM

forest

LSM Forest

1. How will proposer form and maintain a computationally tractable LSM tree structure given, as proposed, hundreds to thousands of observable variables?

\(\checkmark\)

Recursive LSM forest: hyperlinked nodes capturing emergent macro-structures

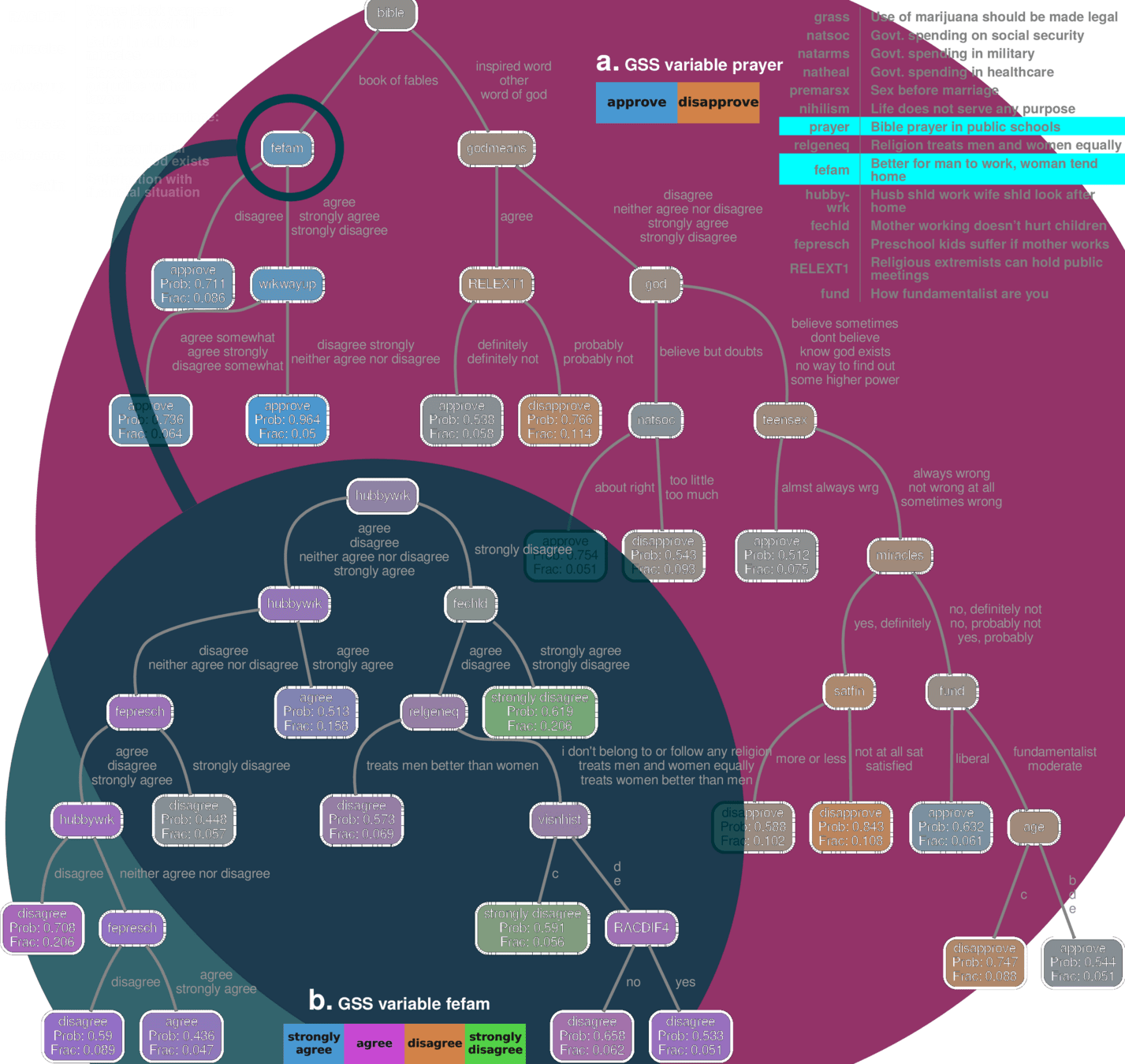
GSS 2018 dataset

  • Set of conditional inference trees (CIT)
    • Strict statistical guarantees: quantifies inference uncertainty
  • Each tree models exactly one variable as a function of potentially all other variables
  • Non-leaf nodes are "hyperlinked" to other trees

Large Science Models

1. How will proposer form and maintain a computationally tractable LSM tree structure given, as proposed, hundreds to thousands of observable variables?

\(\checkmark\)

GSS 2018 dataset

  • Each predictor is inferred independently
  • Can scale up to thousands of variables in Python implementation
  • Further scale-up \(10^6 - 10^8\) needs C/C++ implementation

https://34.66.189.202/data/trees2018/

Full Example  of Hyperlinked Trees

Large Science Models: Mathematical Framework

\begin{aligned} \text{Observables:} \quad & \color{yellow}X = \{x^1, \ldots, x^N\}, \overbrace{x^i \in \Sigma^i}^{\text{finite alphabet}} \\ {\color{gray}\text{Notation:} }\quad & \color{gray} x^{-i} = \{x^j : j \ne i\}\\ \text{Crosstalk:} \quad & \forall i \ P(x^i) = \color{red} f_i(x^{-i}) \\ \text{System state:} \quad & \color{Cyan} \psi = \bigotimes_{i=1}^N \psi^i, \quad \psi^i \in \mathscr{D}(\Sigma^i) \cup \varnothing \\ %\textbf{Degenerate case:} \quad & \psi^i \text{ is a delta distribution (fully observed)} \\ {\color{gray}\text{Notation:} }\quad & \color{gray}\psi^{-i} = \bigotimes_{j \ne i} \psi^j \end{aligned}
reliten  gunlaw abany --- grass
Person 1
Person 2
---
Person m

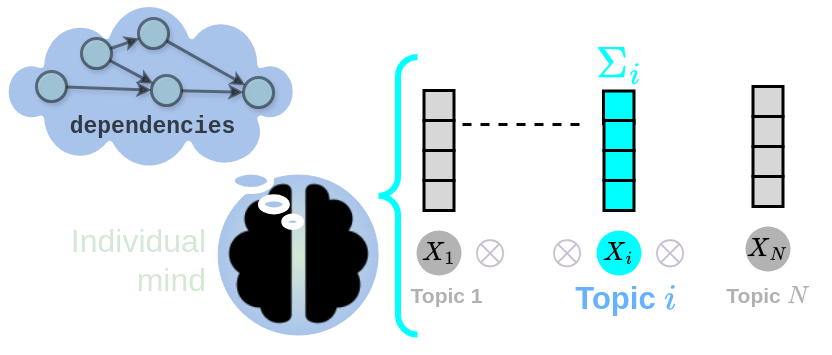
observables

samples

Distributions over alphabet \(\Sigma^i\)

\phi = \bigotimes_{i=1}^N \phi^i, \quad \phi^i(\psi^{-i}) \in \mathscr{D}(\Sigma^i) \\

Individual Predictor (CIT)

cross-talk

\phi(\psi) \vert \vert \psi

Tension between predicted and observed distribution drives change

Example

GSS topic: There should be more gun-control

\(\psi^i\)

strongly agree agree neutral disagree strongly disagree
\Sigma^i

Digital Twin

\phi^i(\psi^{-i}) \sim \widetilde{\psi}^i

\(\phi\) estimates \(\psi\)

Examples: GSS, ANES, WVS, ESS, Eurobarometer, Afrobarometer, Asian Barometer etc

group

individual

estimate is always a non-empty non-degenerate distribution

missing observation

Large Science Models: Properties

LSM-Distance Metric*

\theta(\psi,\psi') \triangleq \frac{1}{N}\sum_{i=1}^{N} \sqrt{D_{JS}\Bigl(\phi^i(\psi^{-i}) \vert \vert \phi^i(\psi'^{-i})\Bigr)}

 where \(D_{JS}(P\vert \vert Q)\) is the Jensen-Shannon divergence.

g_{ij}(\psi) \;=\; \frac{1}{2}\,\frac{\partial^2}{\partial \psi^i\,\partial \psi^j}\,\theta^2(\psi,\psi')\Biggr|_{\psi'=\psi}
\left \lvert \ln \frac{\Pr(\psi\to \psi')}{\Pr(\psi' \rightarrow \psi')}\right \rvert \le \beta\,\theta(\psi,\psi')

Large Deviation Bound*

 Induced  Riemannian metric tensor

This bound connects ``closeness'' of samples to the odds of perturbing from one to the other, bridging geometry to dynamics

Ergodic Projection

\psi_\star \triangleq \bigotimes_{i=1}^N\phi^i\left (\prod_{1}^{N-1}\varnothing\right )

(Sanov's Theorem, Pinkser's Inequality)

\(\psi\)

\(\psi'\)

\(\theta\)

"spatial average":  average of all plausible worldviews or states

* Sizemore, Nicholas, Kaitlyn Oliphant, Ruolin Zheng, Camilia R. Martin, Erika C. Claud, and Ishanu Chattopadhyay. "A digital twin of the infant microbiome to predict neurodevelopmental deficits." Science Advances 10, no. 15 (2024): eadj0400.  https://www.science.org/doi/full/10.1126/sciadv.adj0400

persistence probability

Ergodic dispersion

\Psi_\star = \theta(\psi,\psi_\star)

Central to Model Drift Quantification

Start with opinion vector with all entries missing

This is a standard Physics construct, quantifying curvature of the underlying latent geometry

Pr(\psi \rightarrow \psi')

Easily computable in LSM framework!

Apply \(\phi^i\)

Random variable quantifying dispersion around the spatial average of worlviews

const. scaling as \(N^2\) 

Digital Twin & Fidelity of Simulation

\mathcal{N}_\epsilon(\psi) \triangleq \big\{ \psi': {\color{red}\forall i \ \psi'_i \sim \phi^i\left ( \psi^{-i}\right )} \wedge {\color{yellow} \theta(\psi,\psi') \leqq \epsilon }\big \}

Sample predicted distributions   

perturbed state within \(\epsilon\) of \(\psi\)

Variable Masked Reconstructed
spkcom allowed allowed
colcom not fired not fired
spkmil allowed allowed
colmil allowed not allowed
libmil not remove not remove
libhomo not remove not remove
reliten strong no religion
pray once a day once a day
bible inspired word word of god
abhlth yes yes
abpoor no no
pillok agree agree
intmil very interested very interested
abpoorw always wrong not wrong at all
godchnge believe now, always have believe now, always have
prayfreq several times a week several times a week
religcon strong disagree disagree
religint disagree disagree
Variable Masked Reconstructed
spkcom allowed allowed
colcom not fired not fired
libmil not remove not remove
libhomo not remove not remove
gunlaw favor favor
reliten no religion no religion
prayer approve approve
bible book of fables inspired word
abnomore yes yes
abhlth yes yes
abpoor yes yes
abany yes yes
owngun no no
intmil moderately interested moderately interested
abpoorw not wrong at all not wrong at all
godchnge believe now, didn't used to believe now, always have
prayfreq several times a week several times a week

2018 GSS individual samples

Digital Twin

\(\checkmark\) 8. While you mention digital twins as an end result, please clarify what exactly these twins represent (agents, systems, etc.).\(\dag\)

-Neighborhood of state \(\psi\)

\epsilon

Definition

Sample neighborhood to impute missing data

\psi
\epsilon
}

\(\checkmark\) 5. Provide more details on how you will measure "fidelity of forward simulation" as mentioned in your metrics.**

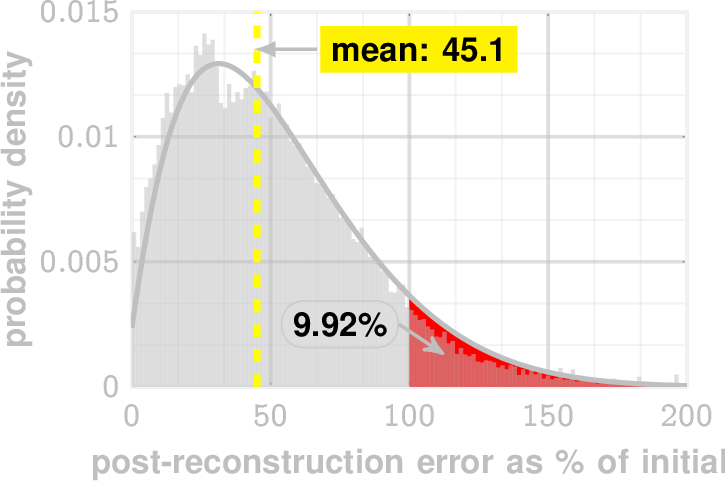
2018 GSS  out-of-sample reconstruction

post-reconstruction error ratio (%)

LSM sampling: sampling the \(\epsilon\)-neighborhood of a state or worldview allows reconstruction of censored opinions

examples

Predictive ability of LSM quantified as ability to reconstruct censored out-of-sample opinions**

{\color{Tomato}\psi_\star }\rightarrow \psi \rightarrow \cdots \rightarrow \psi'

Null state (all missing observations)

Valid perturbations/ simulations

LSM sampling allows simulating opinion perturbations

Both Individuals and groups maybe modeled as digital twins\(\dag\)

Global Emergent Structure via Clusters & Poles

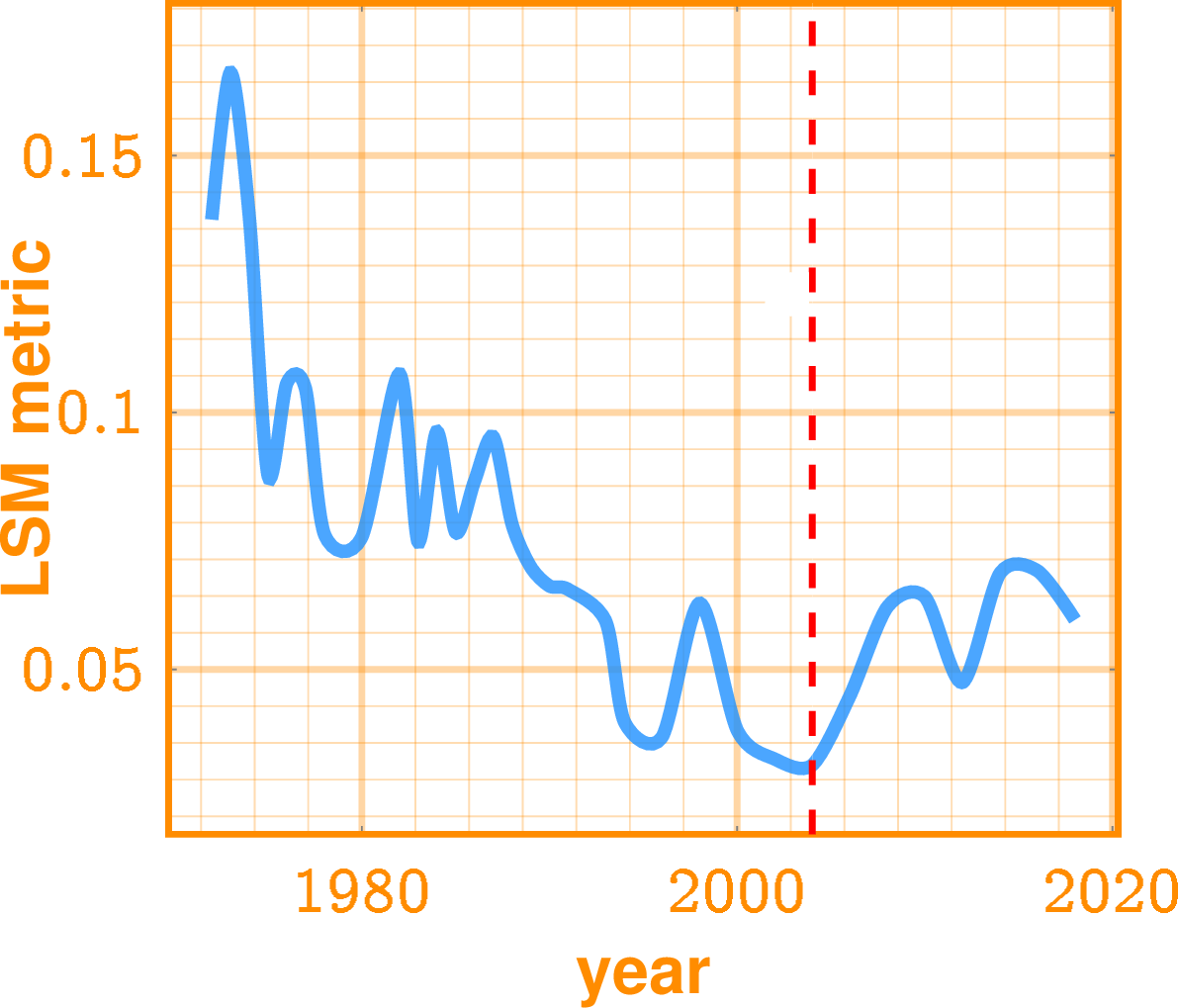
2018 GSS

\theta_t(\psi_+,\psi_-)

Polar separation over time

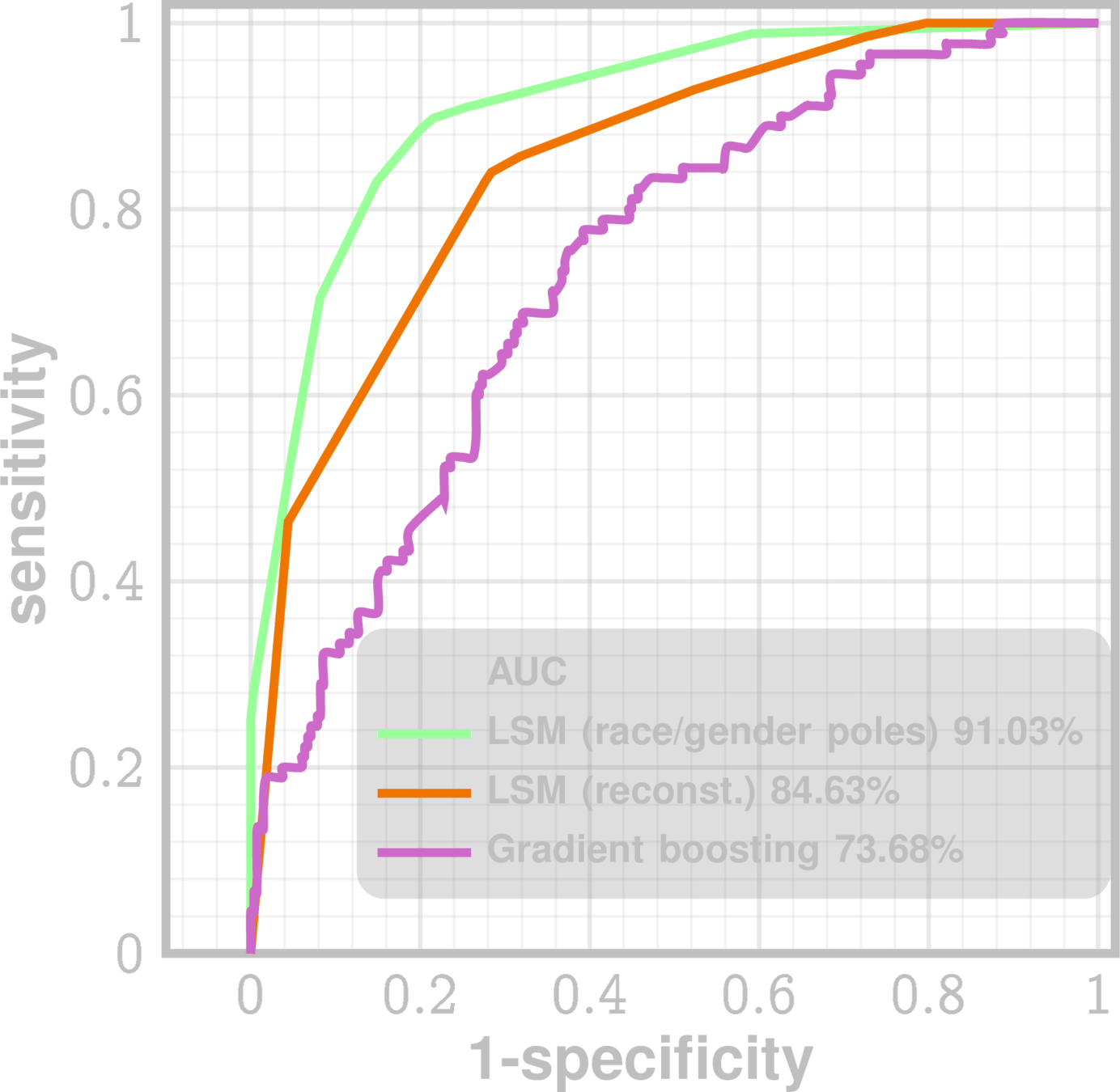
2016 Presidential Election Vote Prediction

2004

abany no yes
abdefctw always wrong not wrong at all
abdefect no yes
abhlth no yes
abnomore no yes
abpoor no yes
abpoorw always wrong not wrong at all
abrape no yes
absingle no yes
bible inspired word book of fables
colcom fired not fired
colmil not fired not allowed
comfort strongly agree strongly disagree
conlabor hardly any a great deal
godchnge believe now, always have don't believe now, never have
grass not legal legal
gunlaw oppose favor
intmil very interested not at all interested
libcom remove not remove
libmil not remove remove
maboygrl true false
owngun yes no
pillok agree strongly agree
pilloky strongly disagree strongly agree
polabuse no yes
pray several times a day never
prayer disapprove approve
prayfreq several times a day never
religcon strongly disagree strongly agree
religint strongly disagree strongly agree
reliten strong no religion
rowngun yes no
shotgun yes no
spkcom not allowed allowed
spkmil allowed not allowed
taxrich about right much too low
     

conservative pole

\psi_+

liberal pole

\psi_-

Clustering LSM distance \(\theta(x,y)\) between out-of-sample individuals

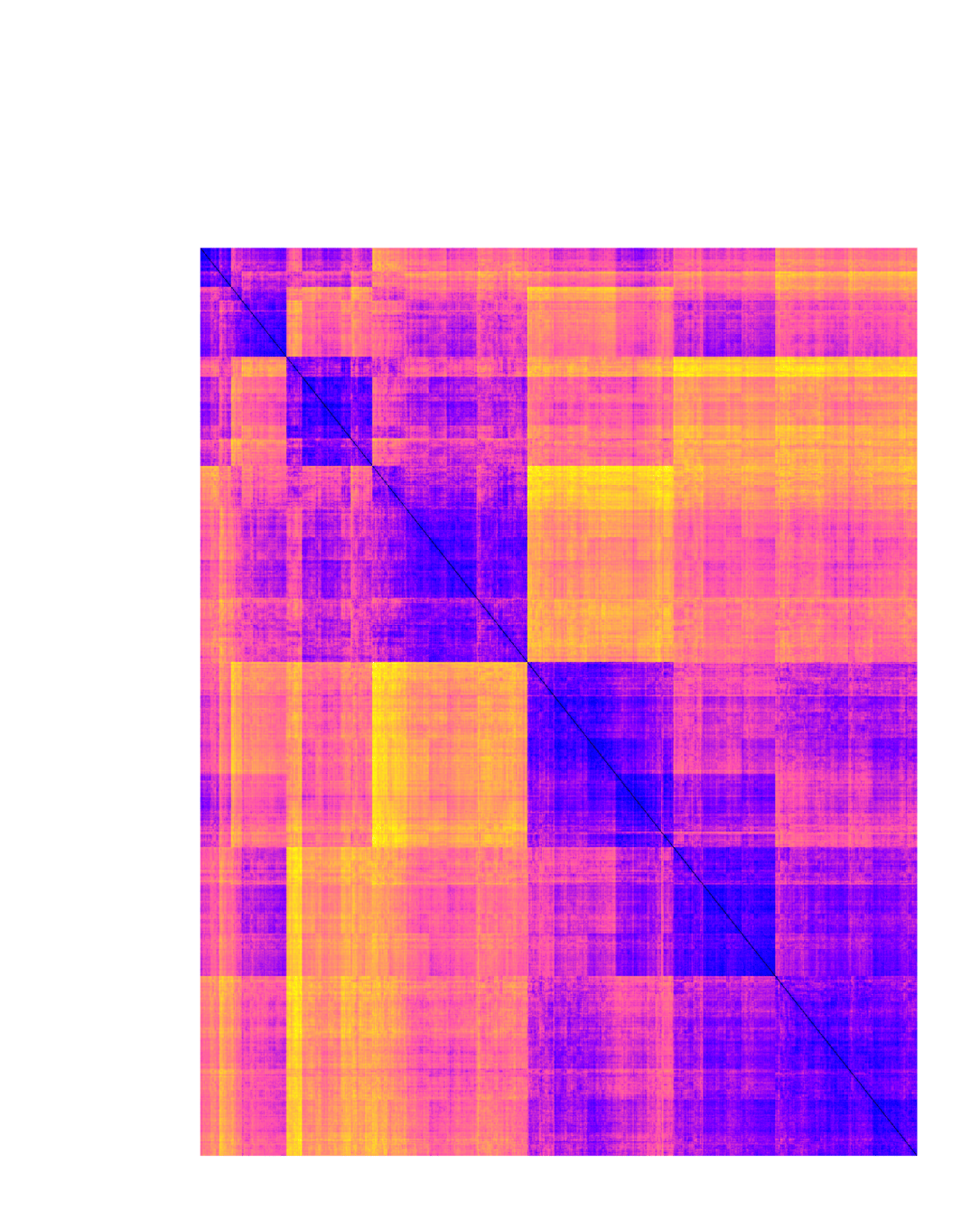
conservative

liberal

poles:

partial states aligning with extreme opposing worldviews

  • Compare across time and different GSS surveys
  • Derived features for individuals (ideology index)
I(x) = \frac{\theta(x,\psi_+) - \theta(x,\psi_-)}{\theta(\psi_+,\psi_-)}

Predict 2016 votes using ideology index

\(\checkmark\) 6. Explain how you will measure the accuracy of predicted structure emergence and data sufficiency.

Emergent global structure

Reflexivity and State Collapse on Observation

Emergent Equations of Motion

L \triangleq \frac{1}{2} \sum_i g_{kl} P^k_p \dot{\psi}^p_i P^l_n \dot{\psi}^n_i - \theta(\psi, \phi)

Define Lagrangian*

\frac{d}{dt} \left( \frac{\partial L}{\partial \dot{\psi}^m_i} \right) - \frac{\partial L}{\partial \psi^m_i} = 0

Via the Euler-Lagrange Equations\(^\dag\):

\ddot{\psi}^m_i = -g^{km} P^k_m \frac{1}{2N} \sum_j \frac{1}{\sqrt{D_{JS}(\psi^m_j \| \phi^m_j)}} \left[ \ln\left( \frac{2e\psi^m_j}{\psi^m_j + \phi^m_j} \right) - \frac{1}{2(\psi^m_j + \phi^m_j)} \right]

Over-damped Gradient flow Equation*

where \(-g^{km}\) is the inverse metric tensor

kinetic energy

state collapse

strongly agree

 agree

neutral

 disagree

strongly disagree

strongly agree

 agree

neutral

 disagree

strongly disagree

Query/

Observation

\(X_i\)

Non-local Influence propagation on measurement/observation (QM-like)

\phi^i(\psi^{-i})

potential energy

* Einstein notation used

Goldstein, Herbert, et al. Classical Mechanics. 3rd ed., Pearson, 2002.

\(^\dag\)

Principle of stationary action

Dynamics

Local potential field eqn

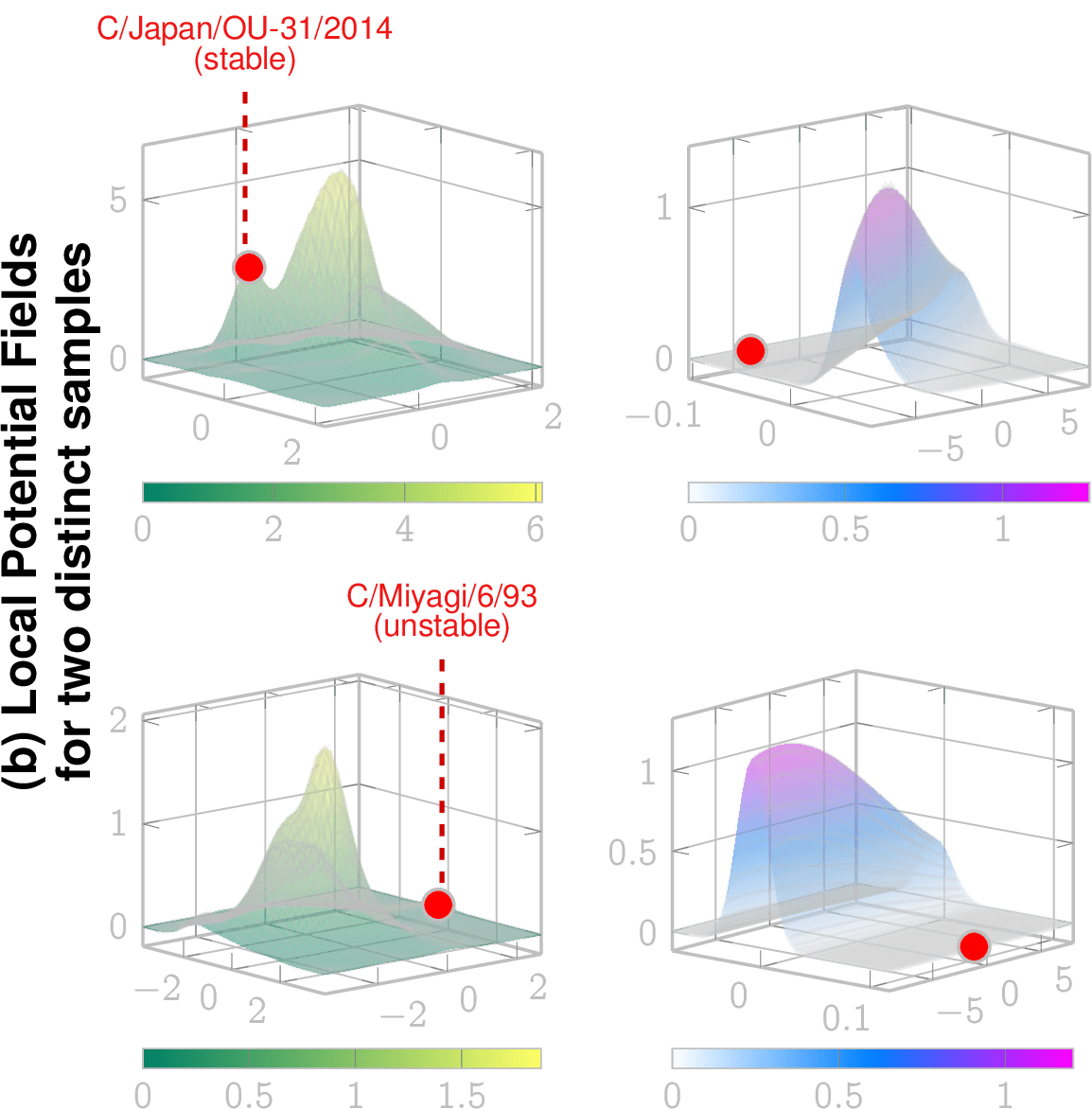
Local Potential Fields

Stable

(captured by local extrema)

Free to move locally towards extrema

Why propaganda works so well

* “Exposure to opposing views on social media can increase political polarization”
by Christopher A. Bail et al., published in PNAS in September 2018 (Vol. 115, No. 37, pp. 9216–9221; DOI: 10.1073/pnas.1804840115)

GSS 2018 individuals and  neighborhoods

Influenza C :  strains and their neighborhoods

Even random perturbations will tend to move individuals towards local extrema increasing polarization

*

  • Polarization is "easy", can occur via random perturbations (falling into the local well)

Hypotheses

Observation: This lineage (Mississippi lineage) is now extinct since 2022/23

stable lineage

Implications on Social Theory

The LSM tells the latent opinion "space-time" how to curve, the curved "space-time" tells opinions how to change.

Local potential fields can be computed given the LSM and dynamical considerations, which reveal future evolution

  • De-polarization is "hard", needs specific communication (climbing up from the well)

Data Sufficiency  via Conservation of Complexity

%K(x) = K(S) + K(x \vert S_\star) + O(1) = K(S') + K(x \vert S'_\star) +O(1) K(x \vert S_\star) = O(1) = K(S \vert x_\star)

The No-cheating Thorem: Generative models cannot cheat on complexity

Kolmogorov Complexity

Optimal Generative Model

compressed data representation

compressed model representation

Theorem

K(\textrm{data}) = K(\textrm{LSM}) +O(1)

Conservation Law arising from the continuous symmetry of typicality*

\mu_0(X) \triangleq \frac{\delta(\vert \langle S(X) \rangle \vert)}{\delta(\vert \langle X \rangle \vert)} \leq 1

Saturation relation:

Data Sufficiency Statistic \(\mu_0\)

We need LSM-sampling to calculate this

*Noether's Theorem

For every continuous symmetry of a physical system, there exists a corresponding conserved quantity

\(\checkmark\) 6. Explain how you will measure the accuracy of predicted structure emergence and data sufficiency.

\vert \langle X' \rangle \vert \approx \max\{1,\mu_0(X)\} \vert \langle X \rangle \vert

How much more data do we need?

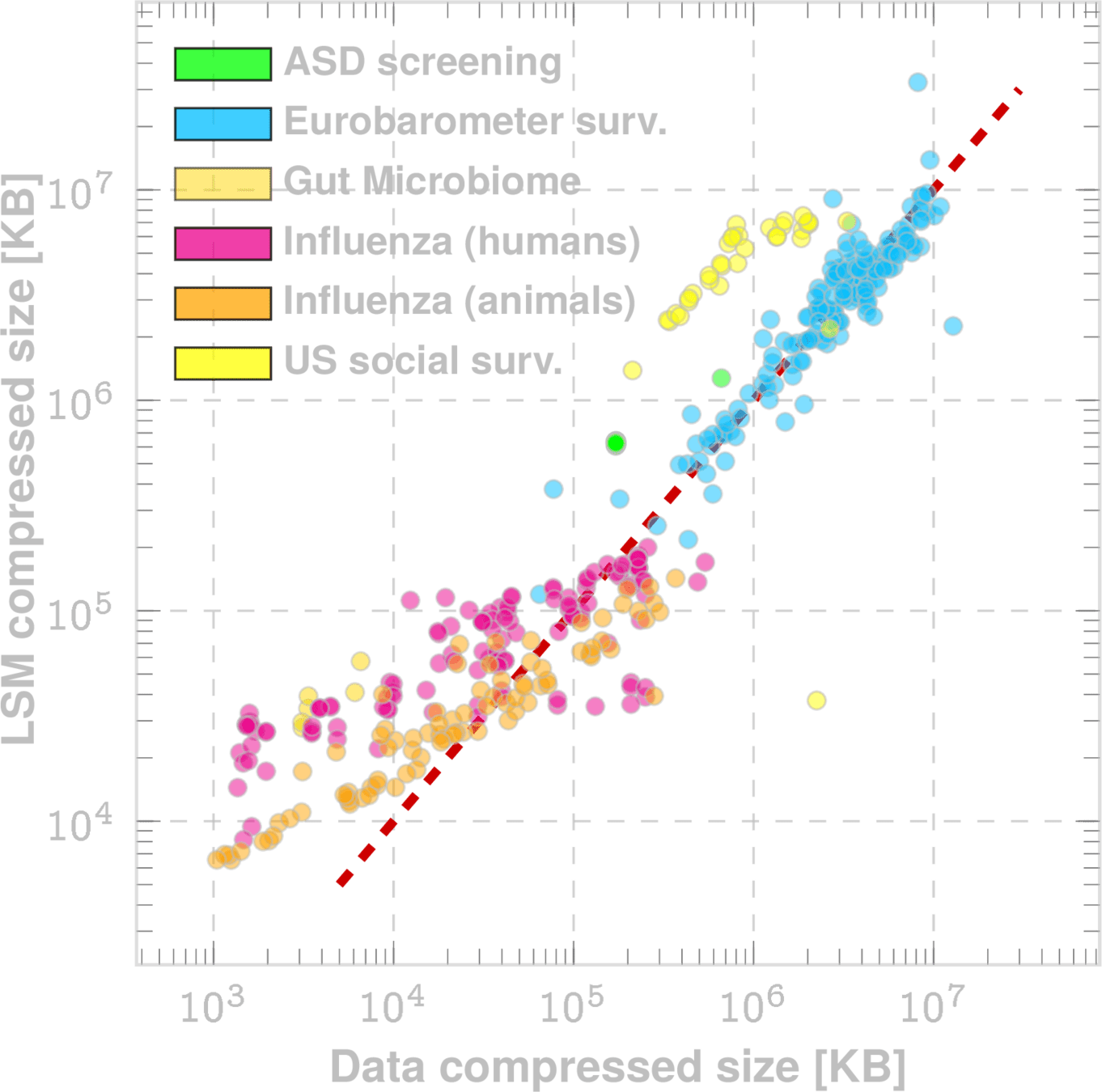
Data saturation

Data deficient

Needed

Current

Empirical Validation

Model Drift Quantification

Ergodic dispersion

\Delta_\star = \theta(\Psi,\psi_\star)
z(\Delta_\star) = \frac{\Delta_\star^{[t]} - \langle \Delta_\star^{[t]} \rangle}{\sigma(\Delta_\star^{[t]} )}

Z-value of dispersion

Do new samples (survey respondents) still conform to the model?

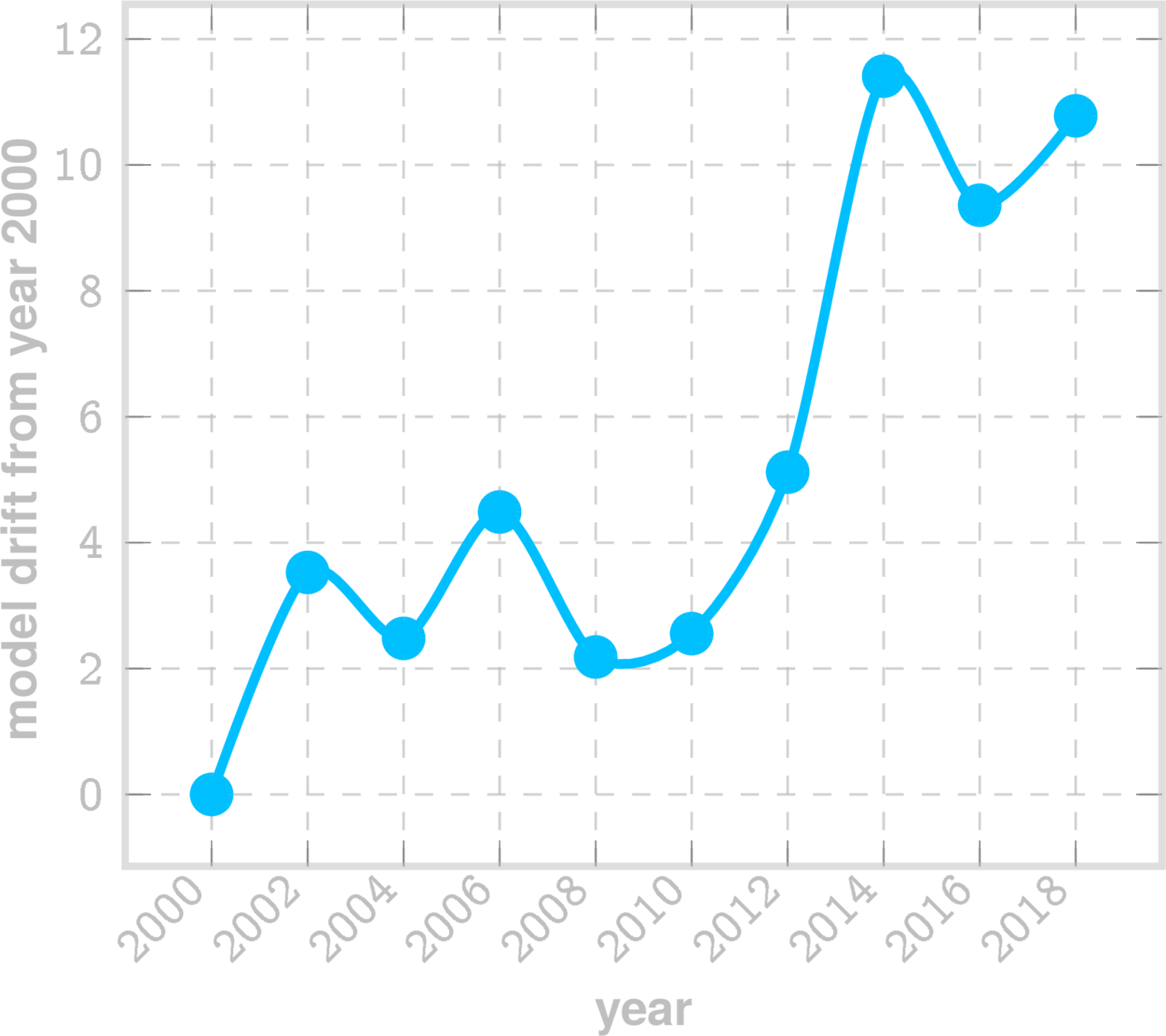
GSS Model drift

\(\checkmark\) 11. Provide more detail on how your model would adapt to or identify significant shifts in system dynamics over time (model drift). 

ergodic projection (all missing values)

A random belief state (with possibly missing entries)

random variable

normal variate

\zeta(M) = \vert z(\Delta_\star^0) - z(\Delta_\star^{[t]}) \vert

Model drift stochastic process (\(\zeta\))

\mathbf{E}(\zeta(M) )

assess if \(\zeta\) is stationary: if not then new samples are not conforming to model

Example for GSS LSM inferred for year 2000

Large Science Models & Ergodicity

\(\checkmark\) 4. Address whether your approach makes assumptions regarding ergodicity, and if so, how these assumptions affect the model's applicability to non-ergodic systems.

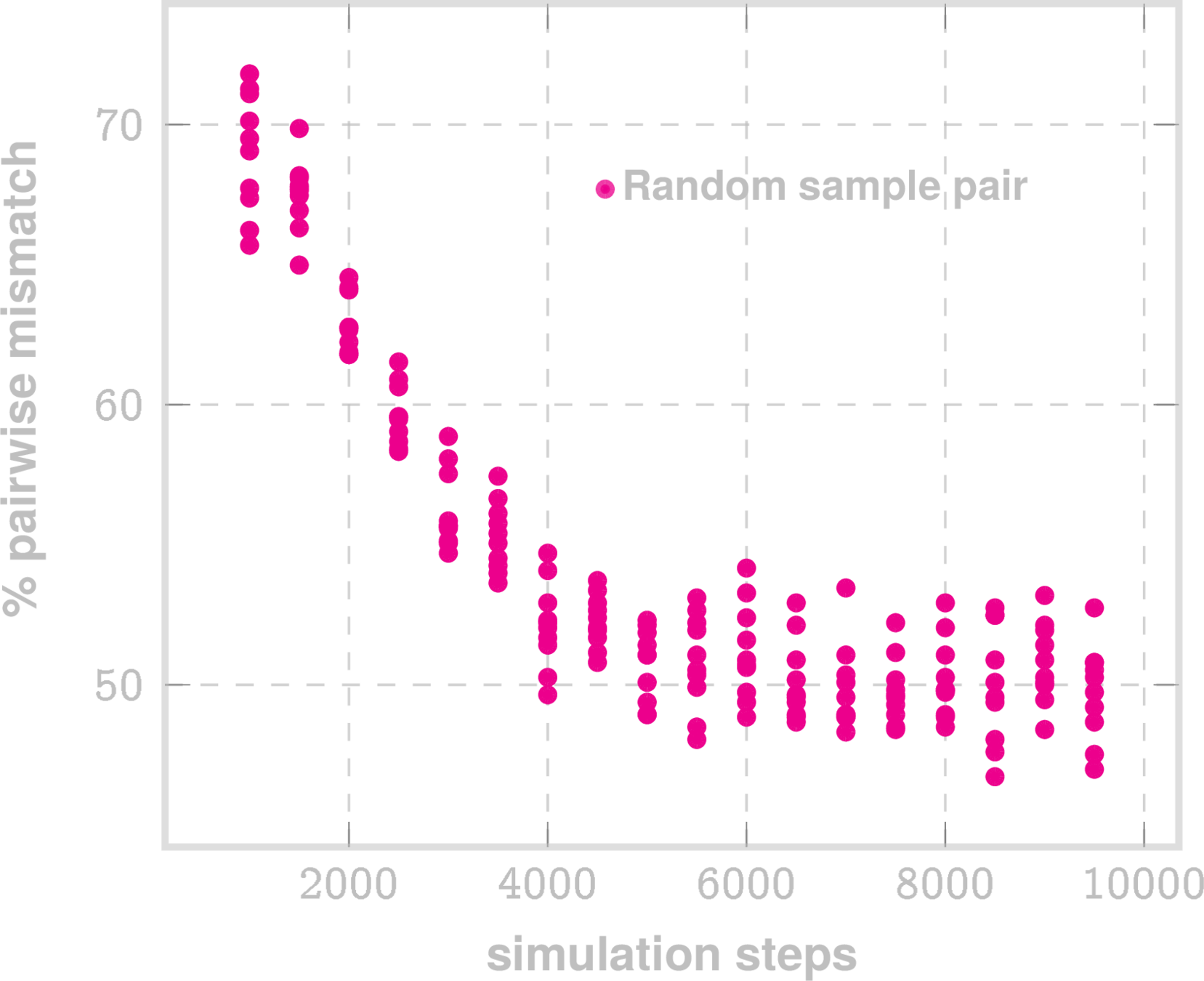
No Convergence

(~50% belief mismatch between pairs)

2018 GSS survey belief vectors simulated via LSM sampling

  • No ergodicity assumption: LSMs are built for non-ergodic systems
  • Sampling and simuation "remembers" the start point (No convergence), demonstrating non-ergodic learned structure
  • Local potential fields vary across the space
  • Potential wells may arise, driven by the dynamics at hand, not via assumptions
  • "change" is driven by non-equilibrium (dissonance)

Embedded Social Theories in LSM

How LSMs reflect and operationalize foundational social-scientific ideas

  • Belief about topic iii is expected to align with beliefs about other topics \(\displaystyle\psi^{-i}\).
    Deviations are exponentially improbable \(\Rightarrow \) people/groups seek internal coherence.

  • Theory Link:

    • Cognitive consistency theory – Abelson et al. (1968)

    • Constraint satisfaction in beliefs – Read & Marcus-Newhall (1993)

  • Beliefs evolve to minimize tension between actual state and “expected” state.
    Reflexive gradient flow — system reduces internal contradiction.

  • Theory Link:

    • Cognitive Dissonance Theory – Festinger (1957)

    • Homeostatic belief adjustment – Gawronski & Strack (2004)

  • Observing a belief changes it and affects all conditionals.
    Direct encoding of feedback loops central to human systems.

  • Theory Link:

    • Reflexivity in social systems – Giddens (1984), Soros (1994)

    • Theory of mind / mutual modeling – Premack & Woodruff (1978)

Validation of Social Theory Questions:

\(\checkmark\) 7. Elaborate on Task 8, particularly how you will test "the ability to adjudicate competing social science theories."

\(\checkmark\) 3. Please clarify how social science theory is integrated into your model. Are theories integrated in some way, or is the model purely data-driven?

  • Perception changes reality, which changes perception
  • The Constitution of Society
  • The Alchemy of Finance
  • Does a chimpanzee have a theory of mind?
  • Our system “wants” to reach a low-energy (low-dissonance) state — a direct computational analog of Festinger’s theory.
  • People strive to align beliefs and attitudes across related domains. Inconsistencies create cognitive discomfort, prompting adjustments across belief clusters to restore harmony.
Exploratory: Belief systems react measurably to exogenous events and shocks

Exploratory: Cross-dependencies between beliefs have observable effects on societal resilience.

Is Polarization an Inevitable Attractor?

Social Identity Theory vs. Belief Proximity

Problem Focus

\(\checkmark\) 2. What specific topic(s) will proposer focus on? E.g. pandemic response hints at DoD-relevant topics but could be more specific.

A General Framework for modeling Complex Systems with Psycho-social Application

Survey Datasets (Public or available at nominal cost)

Survey Waves / Years Avg Participants / Wave Avg Questions / Wave Participants (approx) Data Source / Link
General Social Survey (GSS) ~33 (1972–2024) ~3,000 ~1,500 ~99,000 NORC GSS Data Explorer
ANES ~25 (election-year) ~3,100 ~1,000 ~77,500 ANES Data Portal
Cooperative Election Study (CES) ~18 (2006–2024) ~50,000 ~200 ~900,000 CES Portal
Eurobarometer ~100 (1973–2024, biannual) ~30,000 ~100 ~3,000,000 European Commission Archive
World Values Survey (WVS) 7 waves (1981–2020) ~2,000 / country ~250 ~1,120,000 WVS Website
European Social Survey (ESS) 10 waves (2002–2022) ~2,500 / country ~250 ~750,000 ESS Website
Latinobarómetro ~25 waves (1995–2024) ~18,000 ~110 ~450,000 Latinobarómetro Archive
Afrobarometer 6 rounds (1999–2022) ~1,800 / country ~120 ~220,000 Afrobarometer Archive
Arab Barometer 5 waves (2006–2022) ~1,800 / country ~130 ~135,000 Arab Barometer Site
Asian Barometer 4 waves (2001–2022) ~1,500 / country ~120 ~108,000 Asian Barometer Network

Social Science

Physics

AI

Actionable Validated Theory of Social Dynamics from the individual to groups

DoD Applications: Reliable Forecasts of Human Behavior from Individuals to Collectives|  Communication | De-Radicalization

Psychohistory*

*Asimov, I. (1951). Foundation. New York: Gnome Press.

Future

ARC

Forecast societal opinion shifts

Detect early polarization onset

Map ideological phase transitions

Tailor interventions to subgroups

Optimize persuasion at scale

Digital

Twins of belief systems  /groups

Large Science Models: Broader Applications

\(\checkmark\) 9. Your use case focuses on information transmission through social systems. Could you discuss other potential applications or use cases for your approach? What kind of data would other applications require?

A General Framework for modeling Complex Systems

\(\checkmark\) 10. Discuss any limitations or challenges you anticipate in developing and implementing your LSM framework, and how you plan to address them.

Genomic database: Missing heritability problem

Personalized Clinical Digital Twin, Virtual Patients

Any structured interview, PTSD fabrication

Assess sysmptom data and co-pathologies

Predict future mutations; which animal strain is closest to jumping to humans

Mental health diagnosis

Microbiome Analysis**

Algorithmic lie detector

Viral emergence

Teomims

Opinion Dynamics

Darkome

Generative model of complex microbial ecosystems, and their impact on health and disease

Data requirements

  • Tabular data
  • Potentially large number of features/covariates (\(10^2 - 10^8 \))
  • Sufficient number of samples (\(10^3 - 10^6\))
  • Small number of longitudinal samples (currently, \( < 100\))
Limitation Mitigation / Response
Conventional time series is currently out-of-scope Focus on cross-sectional interdependencies and belief geometry; time handled via drift
LSMs model statistical interdependence, not causal mechanisms Use perturbation-based simulations to infer plausible influence pathways
Limited by observed belief variables Integrate multiple surveys; use latent proxies and test sensitivity of digital twins
Social theory connections and interpretability may be challenging Anchor dynamics with theory-driven constructs (e.g., ToM, cognitive dissonance)

LSMs for complex systems

**preliminary study published (https://www.science.org/doi/10.1126/sciadv.adj0400)

Proposer Overview       

PI: Ishanu Chattopadhyay, PhD

Assistant Professor of Biomedical Informatics & Computer Science

Associate Faculty Sanders-Brown Center of Aging

University of Kentucky

  • PI on 4 past DARPA grants
    • D3M (Data-driven Discovery of Models, I20, PM: Wade Shen)
    • PAI (Physics of AI, DSO, PM: James Gimlett)
    • PREEMPT (PREventing EMerging Pathogenic Threats, BTO, Site-PI, PM: James Gimlett)
    • YFA 2020 (Topic: Cognitive Dissonance, PM: Bartlett Russell)
  • High impact publications (https://scholar.google.com/citations?user=JpUbOmsAAAAJ&hl=en)
    • Nature Human Behavior
    • Science Advances
    • Nature Communication
    • PNAS
    • Nature Medicine
  • Funding from Alzheimer's Association, NIA
  • Advised 3 Postdocs, 2 PhD, over 30 graduate and undergraduate students
  • >40 Invited lectures including at NIH, DoD Facilities, National Labs

Staff Scientist (TBD) w expertise:

  • ML/AI
  • Stochastic processes
  • Software Implementation in C++/Python

Existing PhD Student

(Not funded by ARC)

  • ML/AI                                            
  • Stochastic processes

The computational facilities available to Biomedical informatics, CS at UKy, along with its research infrastructural support will ensure smooth execution.

Current members of the Chattopadhyay Lab (ZeDlab) will contribute to program success, while not being directly funded:

Other Support

Cost & Schedule               

Estimated costs USD
Labor cost 157,227.86
Other direct costs 9,993.00
Total (direct+indirects for 12 months) 257,520.12

Validation Plan Outline

Gantt Chart*

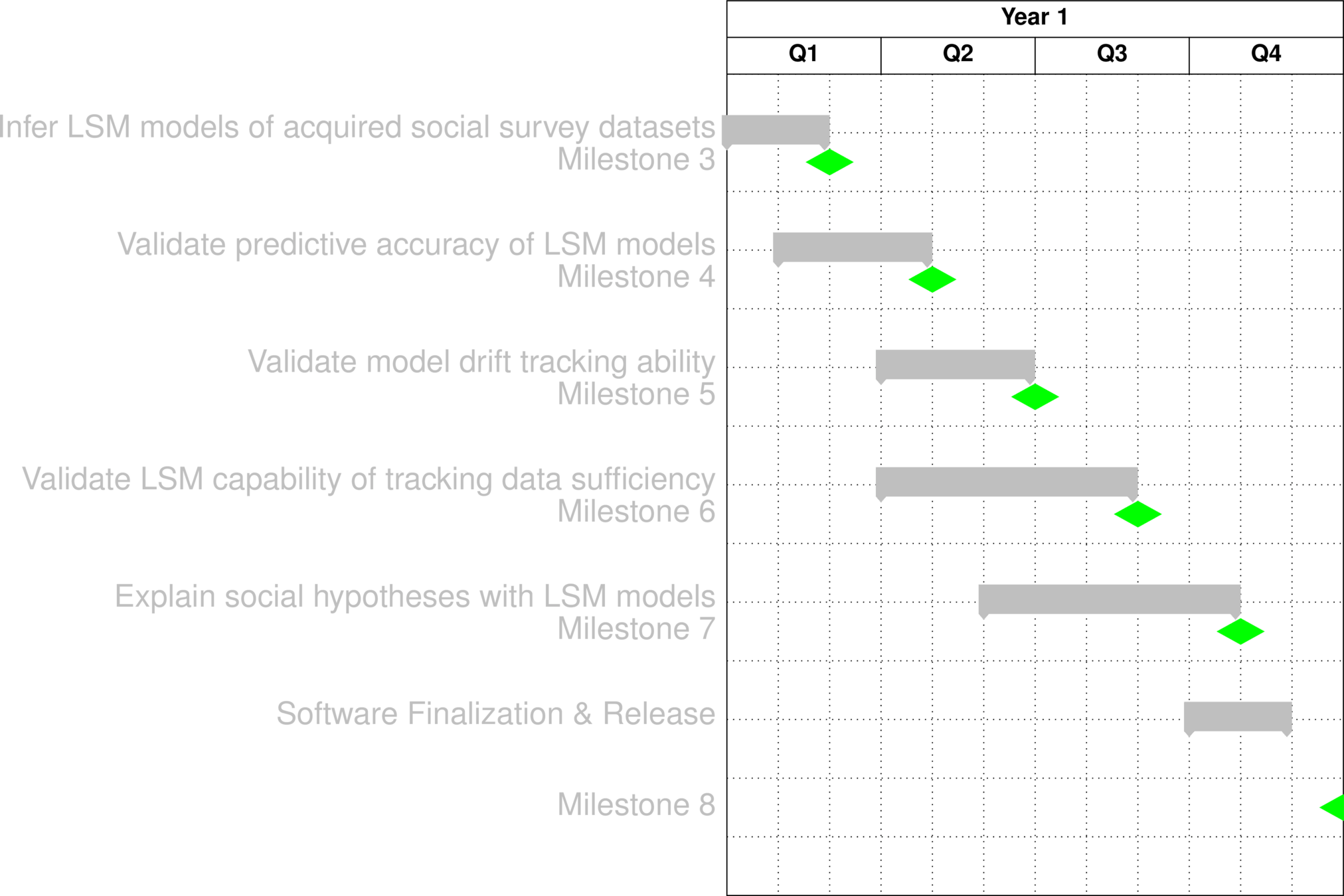
*Milestone definitions in next slide

Dataset Acquisition (10 survey datasets)

LSM inference

LSM predictive ability validation

LSM model drift sense validation

LSM data sufficiency tracking validation

LSM mediated social theory analysis

Milestones                           

1 Kickoff Meeting: A briefing on the technical plan for the effort to include milestone schedule and path to accomplish the objectives of the agreement. Government acceptance / Kickoff meeting briefing slides Month 1 after award start
2 Validation plan: Detailed validation plan, including description,acquisition plan, and justification for the ground truth data, and description of the metricsand benchmarks to be used to measure performance. Government acceptance / Technical report as described. Month 1
3

Milestone Title: Dataset Acquisition and LSM Inference

Technical goal: a) Dataset acquisition (10 social survey datasets acquired: GSS, ANES, CES, Eurobarometer etc) b) Infer LSM models for each dataset using 50% random samples, multiple LSMs trained with different random splits for each dataset.

 Government acceptance / Technical report detailing figure/code/data/etc. and all underlying materials generated in support of milestone, regardless of success Month 2
4

Milestone Title: Masked sample reconstruction

Technical goal: LSM predictive accuracy validation via censored sample reconstruction validation on out of sample data from each dataset, Demonstrate statistically significant reduction of LSM distance post reconstruction relative to post-masking. Target: Reconstruction metric error at least 50% improvement over 1) random imputation 2) median imputation

 Government acceptance / Technical report detailing figure/code/data/etc. and all underlying materials generated in support of milestone, regardless of success Month 4
5

Milestone Title: Model drift sensing validation

Technical goal: Demonstrate that LSM framework can reliably sense when underlying model drifts. Assess if the model drift statistic is stationary from samples drawn from the same survey wave of our datasets, and reliably indicates non-stationary drift for samples from different survey waves. Target: Model drift statistic must have statistical significance at 5% level for survey waves 5 years apart for at least GSS, CES and Eurobarometer Deliverable are detailed documentation on all 10 datasets

 Government acceptance / Technical report detailing figure/code/data/etc. and all underlying materials generated in support of milestone, regardless of success Month 6
6

Milestone Title: Data sufficiency assessment capability

Technical goal: Use the conservation of complexity principle to show that LSM framework can sense data deficiency and sufficiency.

 Government acceptance / Technical report detailing figure/code/data/etc. and all underlying materials generated in support of milestone, regardless of success.Analysis results on all 10 datasets Month 8
7

Milestone Title: Social Theory and Competing Hypotheses Adjudication

Technical goal: a) Social Theory Hypothesis Assessment: Polarization is an inevitable attractor b) Investigate the competing hypotheses that socio-economic identity vs belief proximity and latent opinion space geometry is more predictive of specific opinion / belief outcomes

 Government acceptance / Technical report detailing figure/code/data/etc. and all underlying materials generated in support of milestone, regardless of success Month 10
8

Final milestone meeting and report (one month prior to award end date): The final briefing and final report should summarize all work completed on the project, highlighting accomplishments, lessons learned, unexpected outcomes, and challenges requiring further Research.

Technical artifact delivery (Software release, evaluation results, source code, models, etc.)

 Government acceptance / Technical report as described.For software: Github repository with deployable code complete with example notebooks Month 11

Milestone Title / Detailed Description

Exit Criteria /Deliverable

Due Date (nlt)

Milestone #