From zero to generative

From Zero to Generative

IAIFI Fellow, MIT

Carolina Cuesta-Lazaro

Art: "The art of painting" by Johannes Vermeer

Learning Generative Modelling from scratch

p(\mathrm{World}|\mathrm{Prompt})

["Genie 2: A large-scale foundation model" Parker-Holder et al]

p(\mathrm{Drug}|\mathrm{Properties})

["Generative AI for designing and validating easily synthesizable and structurally novel antibiotics" Swanson et al]

Probabilistic ML has made high dimensional inference tractable

1024x1024xTime

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

https://parti.research.google

A portrait photo of a kangaroo wearing an orange hoodie and blue sunglasses standing on the grass in front of the Sydney Opera House holding a sign on the chest that says Welcome Friends!

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

BEFORE

Artificial General Intelligence?

AFTER

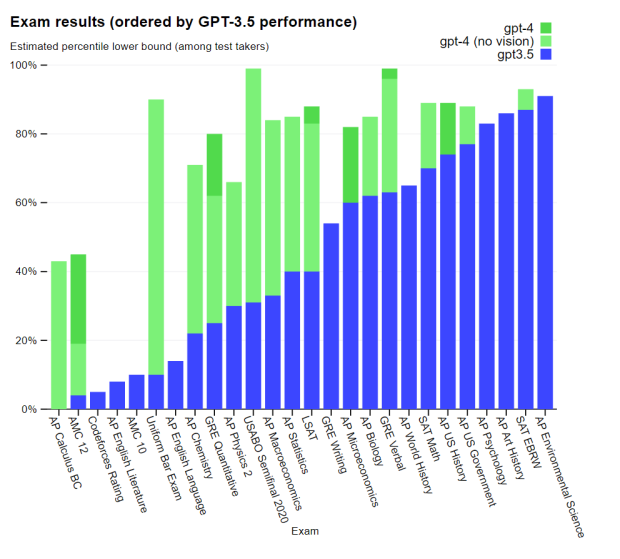
Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Scaling laws and emergent abilities

"Scaling Laws for Neural Language Models" Kaplan et al

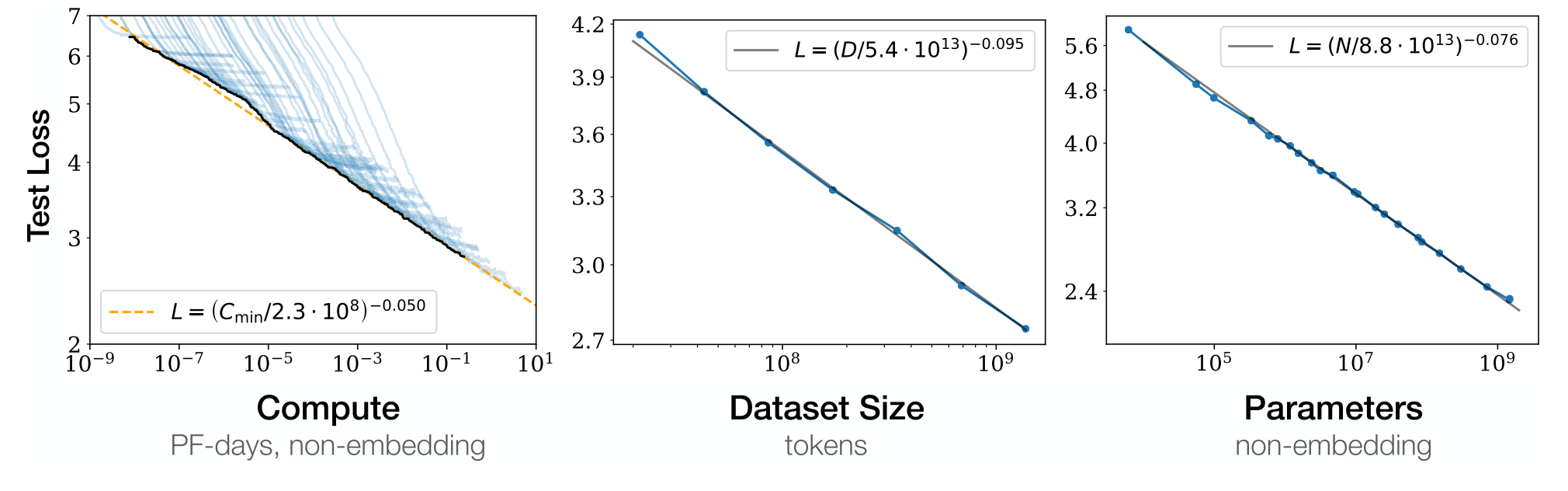
Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

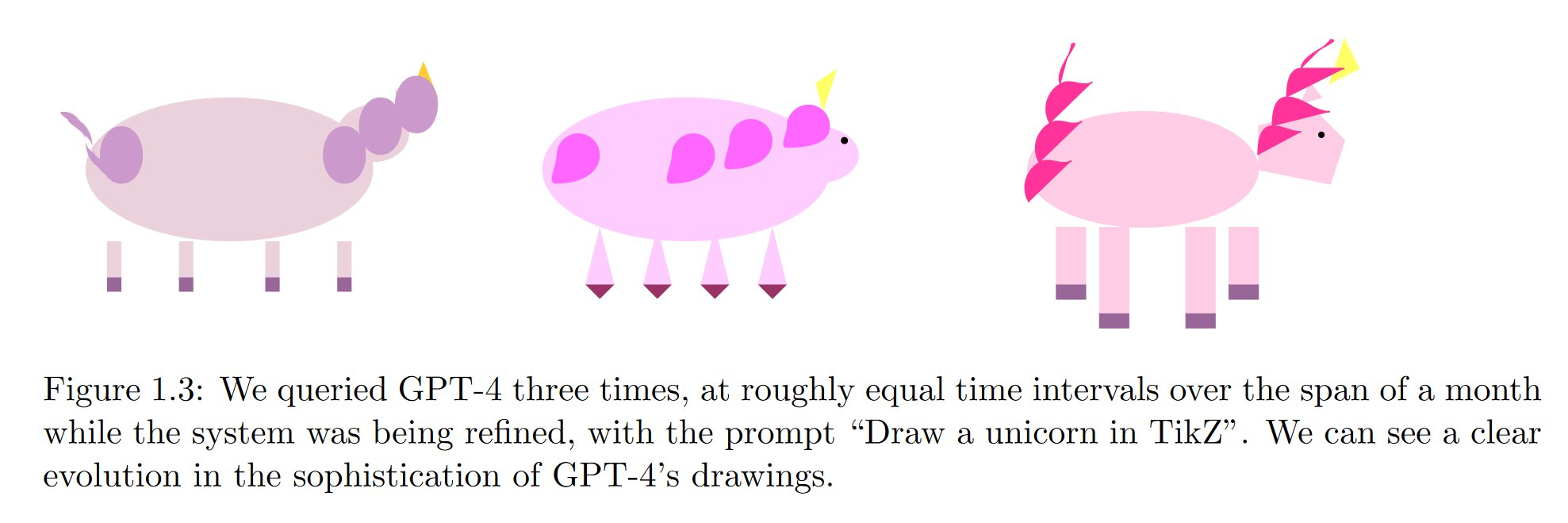
"Sparks of Artificial General Intelligence: Early experiments with GPT-4" Bubeck et al

Produce Javascript code that creates a random graphical image that looks like a painting of Kandinsky

Draw a unicorn in TikZ

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Today's Plan

1. Machine Learning building blocks

2. Tutorial: Build your first classifier

BREAK

4. Introduction to Generative Models

5. Tutorial: Build your first generative model

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

The building blocks: 1. Data

Cosmic Cartography

(Pointclouds)

MNIST

(Images)

Wikipedia

(Text)

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

1024x1024

The curse of dimensionality

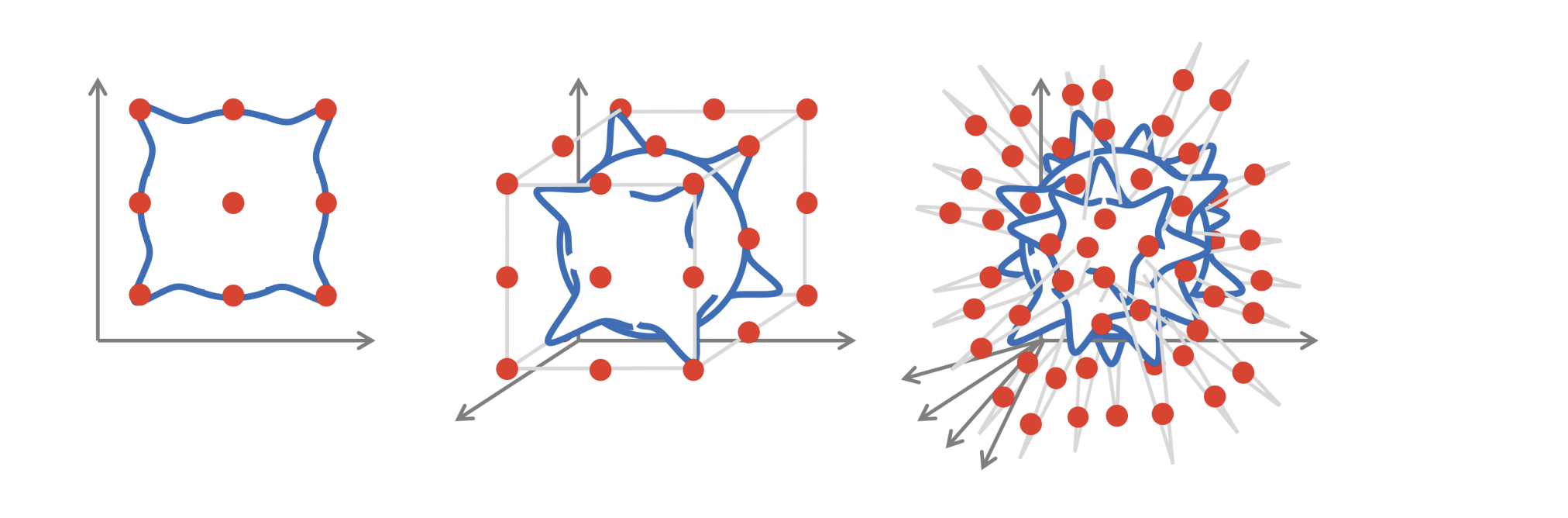
Inductive biases!

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

The building blocks: 2. Architectures

"Geometric Deep Learning Grids, Groups, Graphs, Geodesics, and Gauges" Bronstein et al

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Image Credit: CS231n Convolutional Neural Networks for Visual Recognition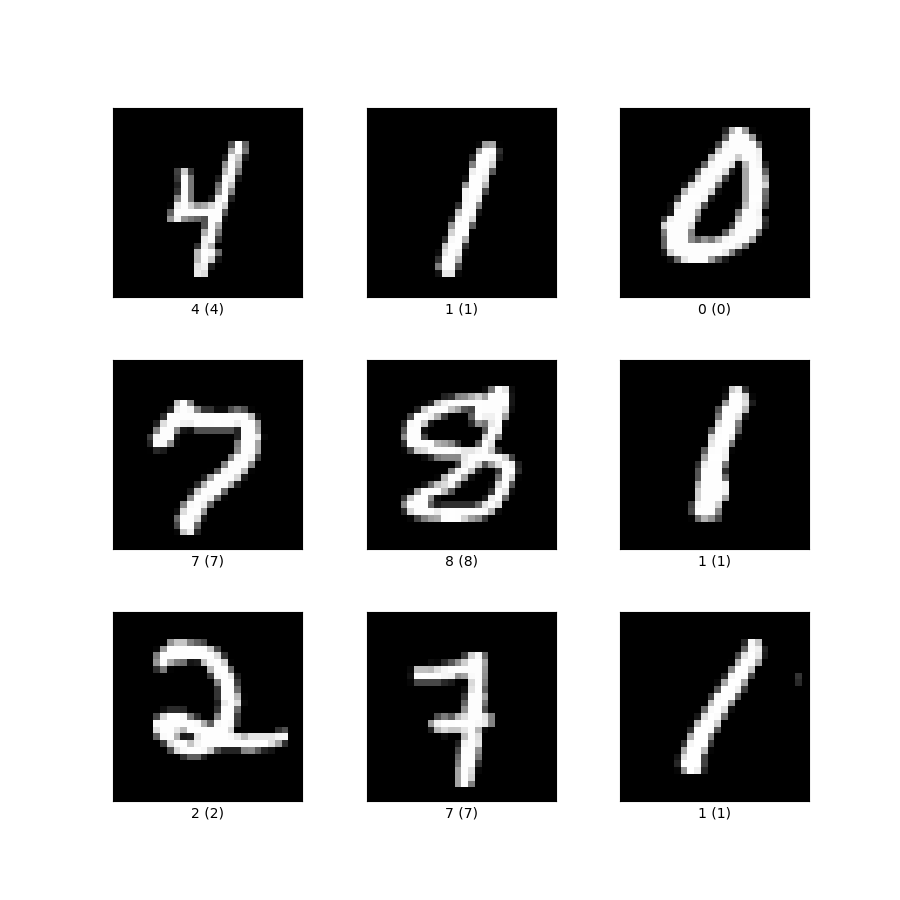

Pixel 1

Pixel 2

Pixel N

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

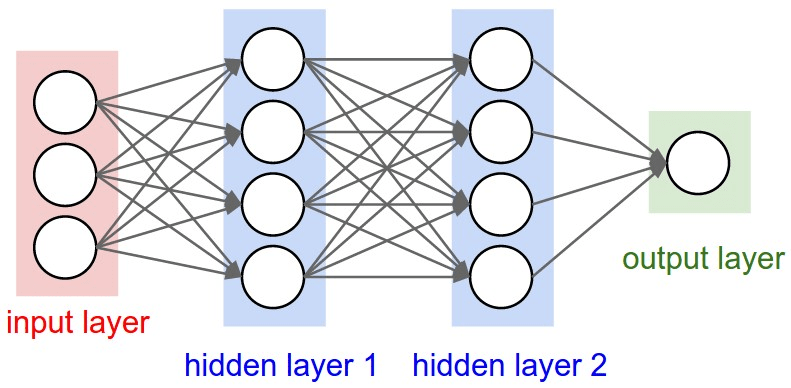
Multilayer Perceptron (MLP)

a^{(l)} = f^{(l)}(W^{(l)}a^{(l-1)} + b^{(l)})

Inductive bias: Translation Invariance

Data Representation: Images

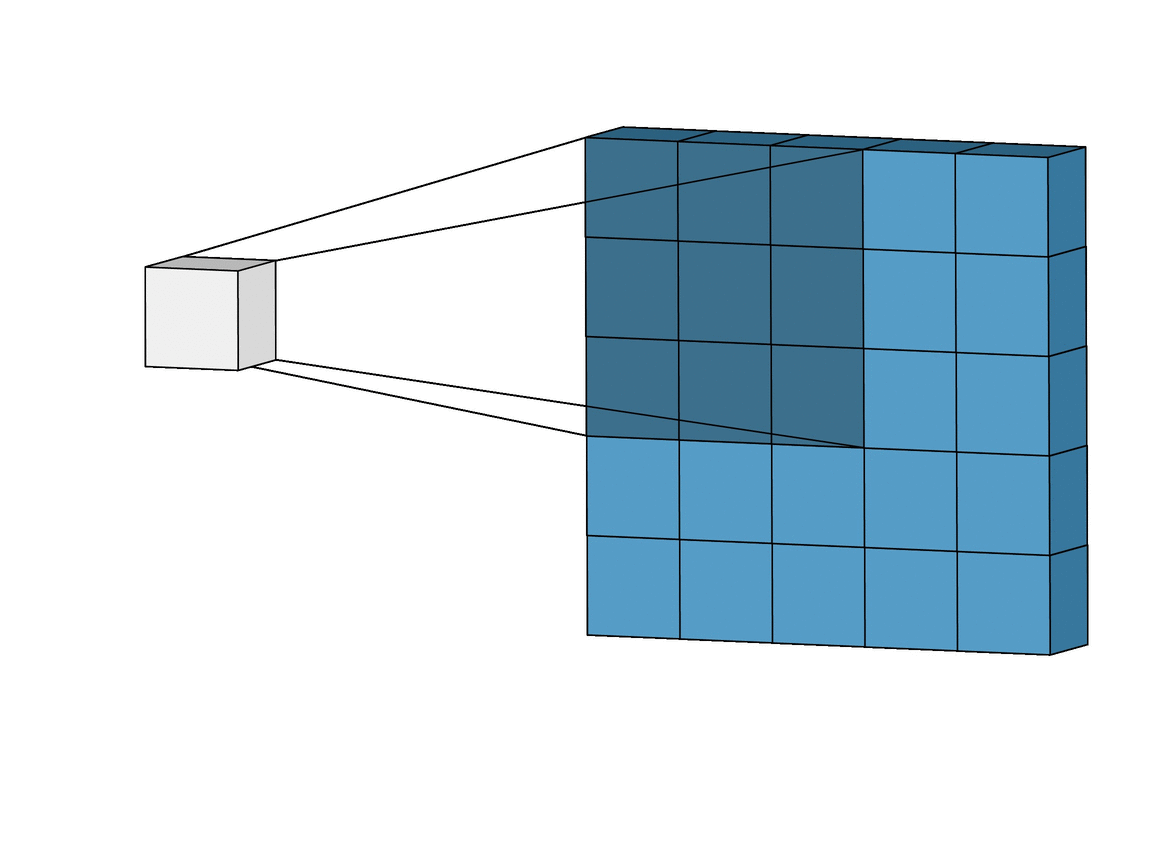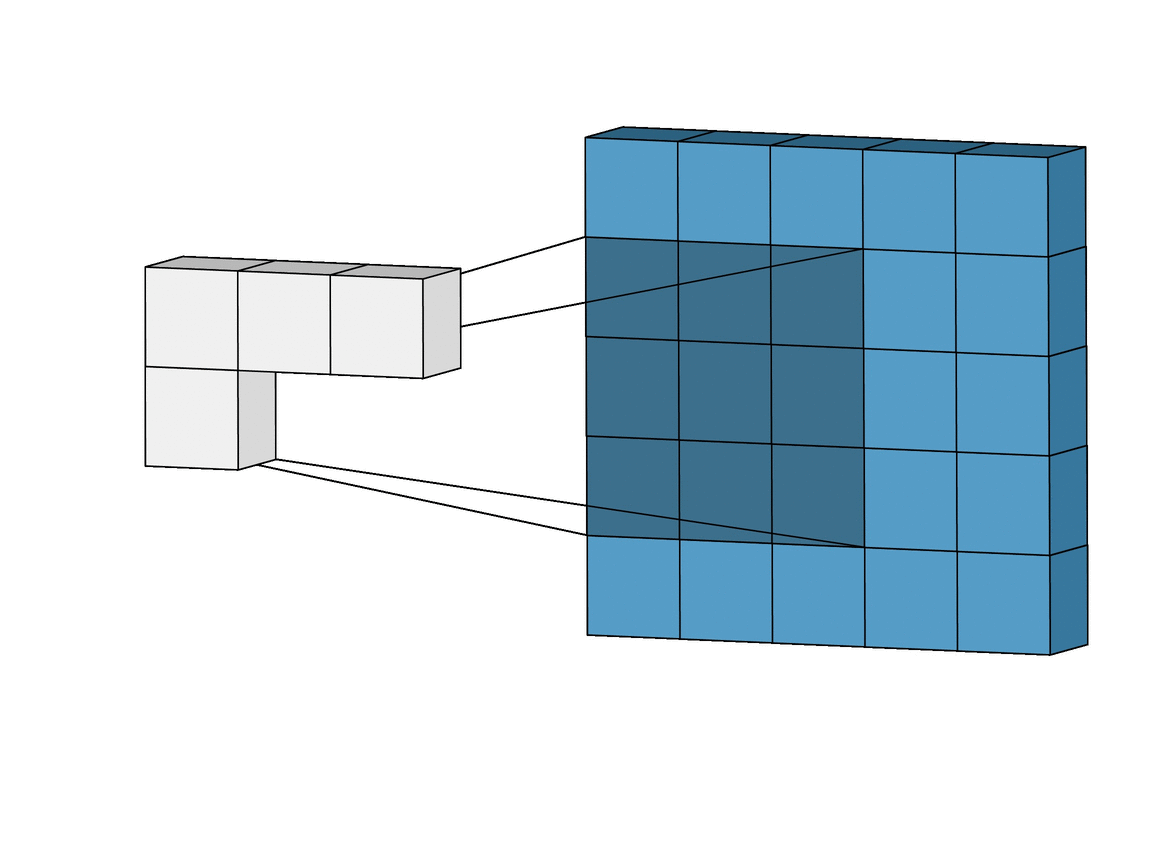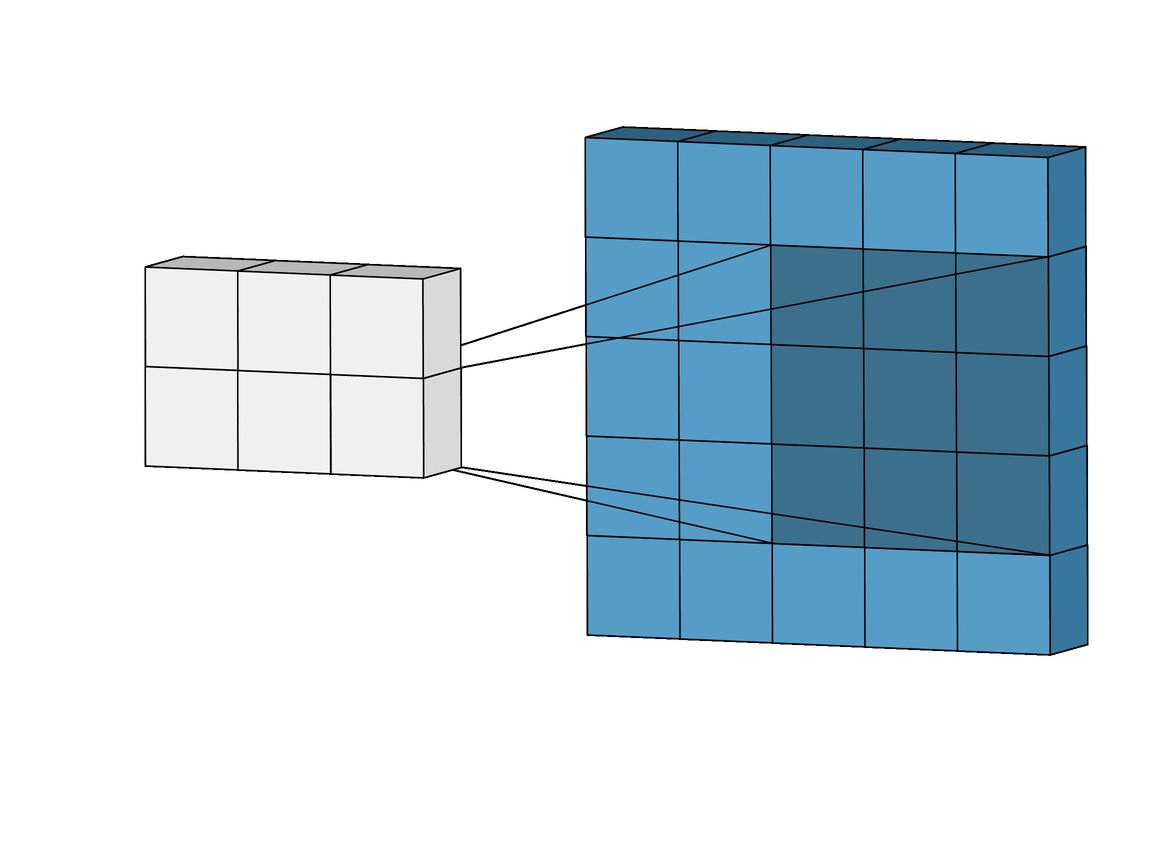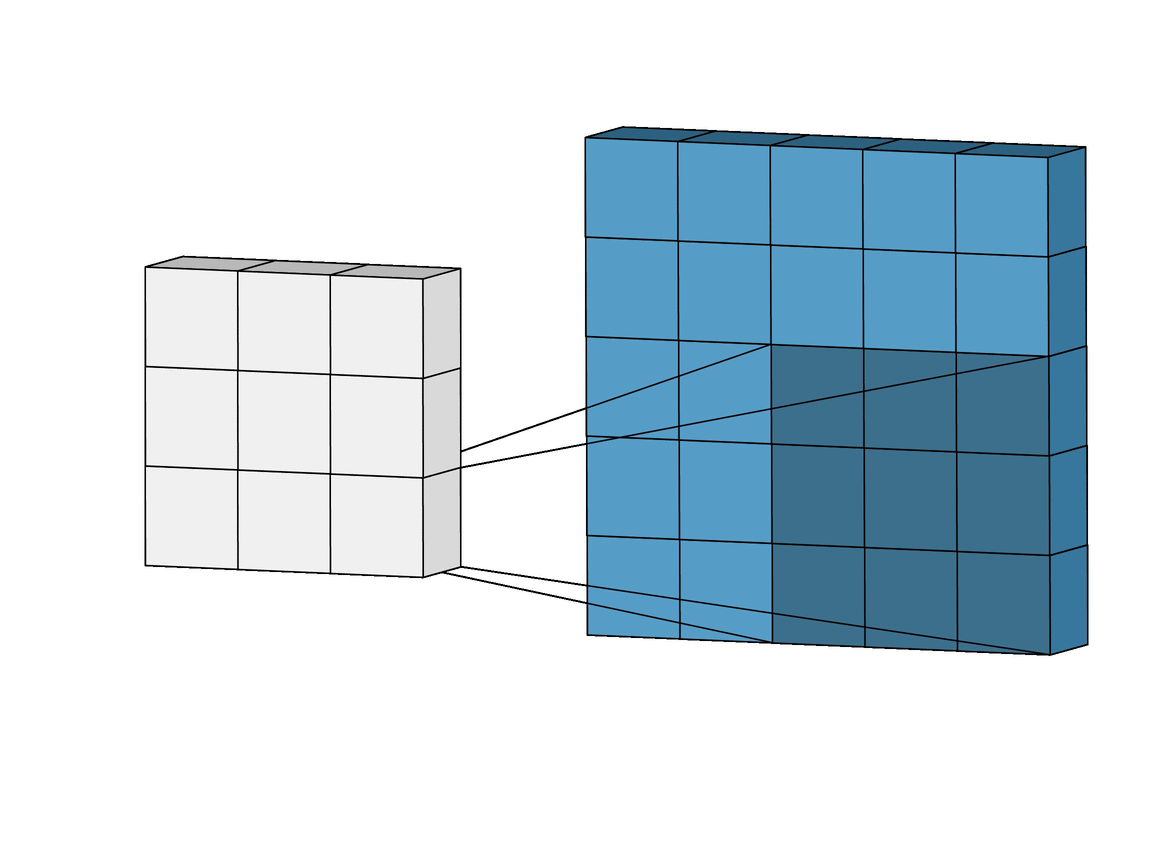
Image Credit: Irhum Shakfat "Intuitively Understanding Convolutions for Deep Learning"

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Convolutional Neural Network (CNN)

Inductive bias: Permutation Invariance

Data Representation: Sets, Pointclouds

= 4

f(x) = f(P(x))

f(x) = \oplus_{i=0}^N h_\theta(x_i)

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

= 4

Deep Sets

Text

Images

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

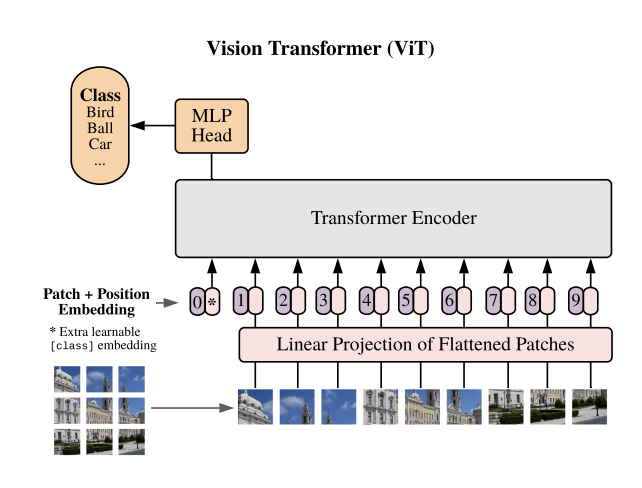
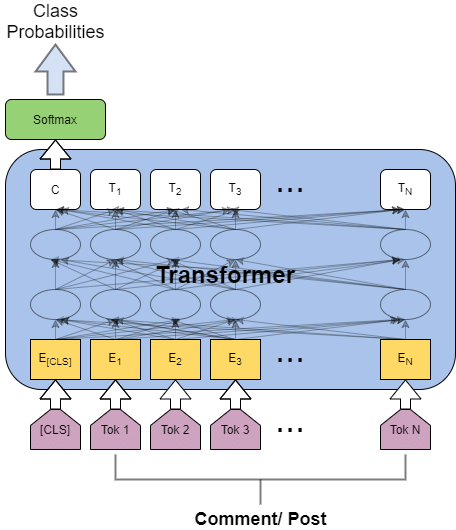
Transformers

The Unifying architecture?

Inductive bias: Permutation Invariance

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V

Input token

QUERY: What is X looking for?

KEY: What token X contains

VALUE: What token X will provide

"The dog chased the cat because it was playful."

W_Q

W_K

W_V

Q = W_Q \times x

K = W_K \times x

V = W_V \times x

But, we decide to break permutation invariance!

Positional Encodings

"Dog bites man"

"Man bites dog"

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

PE_{(\text{pos}, 2i)} = \sin\left(\frac{\text{pos}}{10000^{2i/d_{\text{model}}}}\right)

PE_{(\text{pos}, 2i+1)} = \cos\left(\frac{\text{pos}}{10000^{2i/d_{\text{model}}}}\right)

The building blocks: 3. Loss function

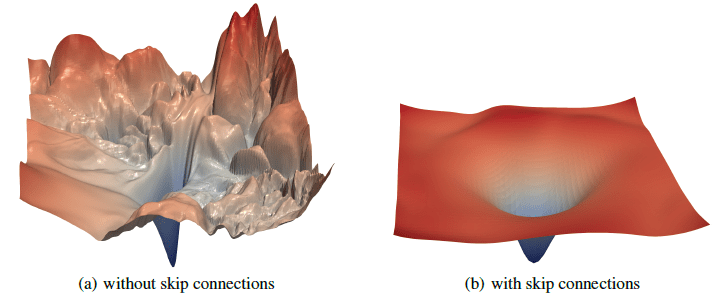
Image Credit: "Visualizing the loss landscape of neural networks" Hao Li et al

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

The building blocks: 4. The Optimizer

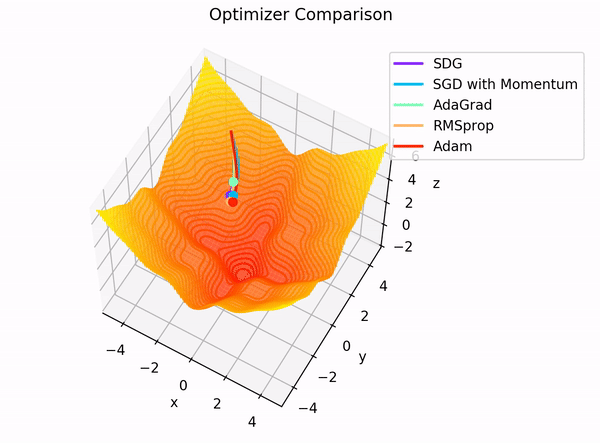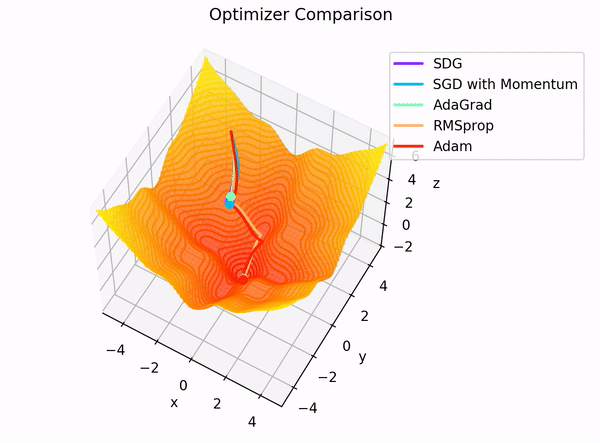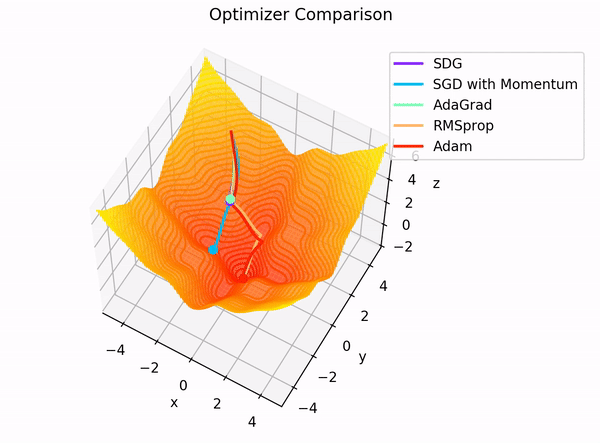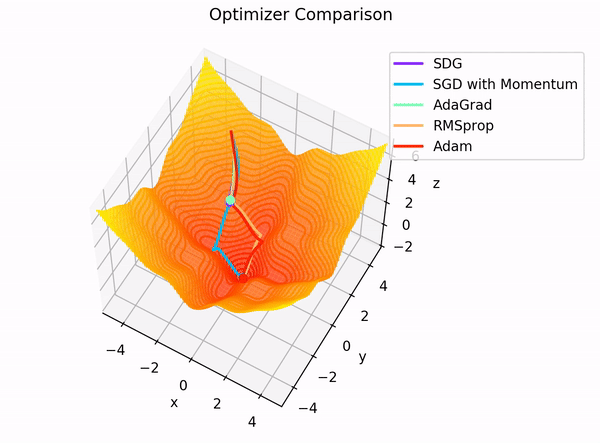
Image Credit: "Complete guide to Adam optimization" Hao Li et al

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Tutorial 1: Learning to classify

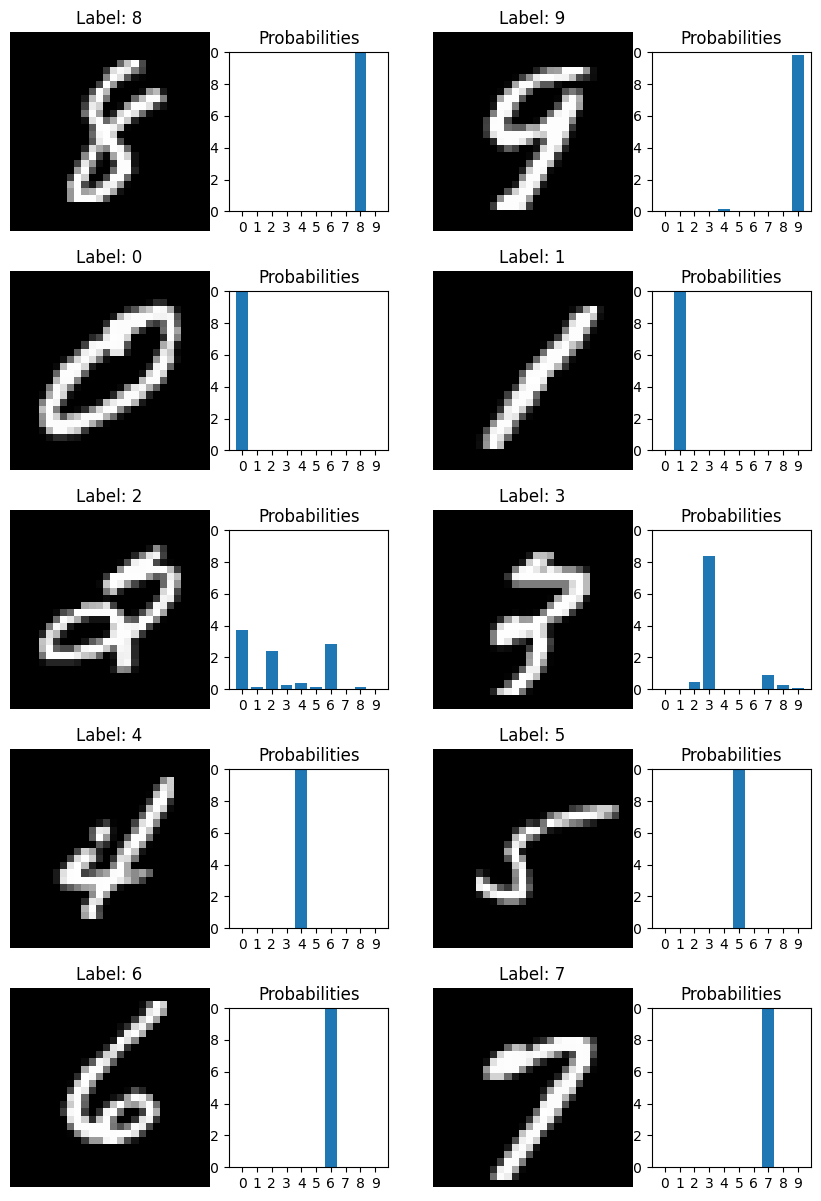
Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

How do we output a probability?

0 \leq p_i(x) \leq 1

\sum_i^C p(x_i) = 1

\text{softmax}(z_i) = \frac{e^{z_i}}{\sum_{j=1}^K e^{z_j}}

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

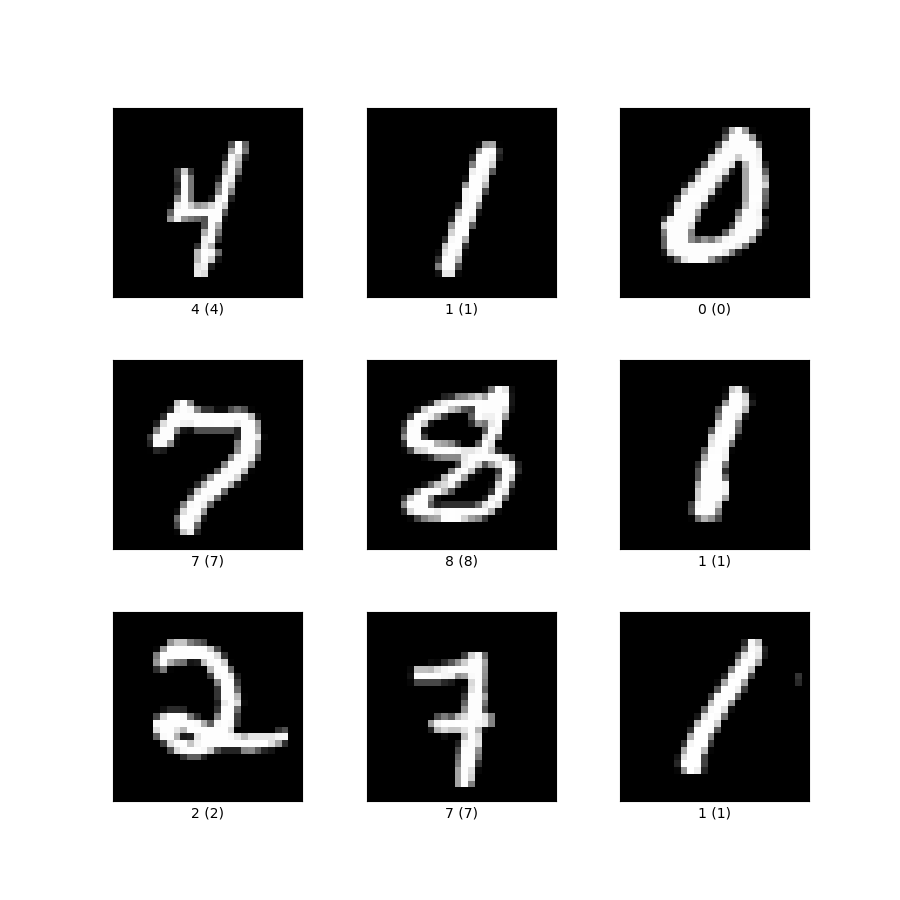
Pixel 1

Pixel 2

Pixel N

p Class 1

p Class 2

p Class 10

Loss function: Cross entropy

How different are two probability distributions?

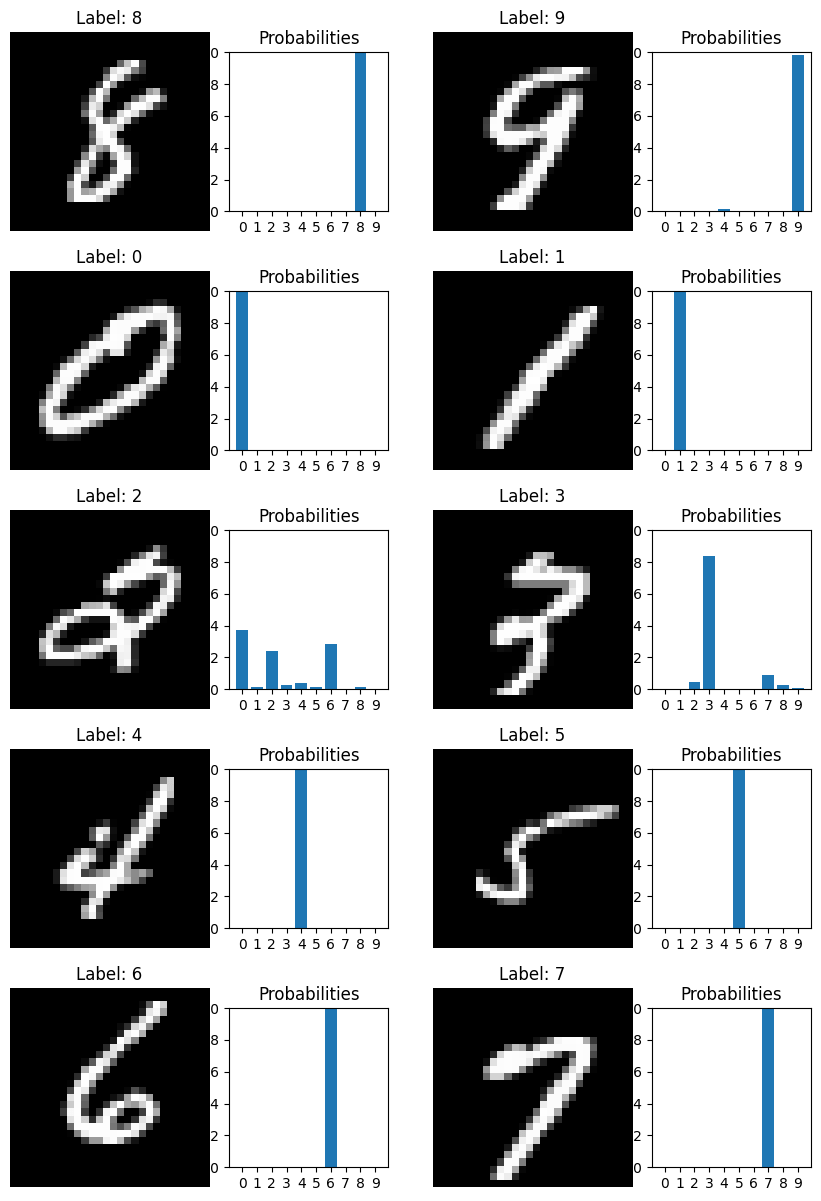
Model Prediction

if True class is for i

y_{i} = 1

y_{i} = 0

otherwise

L = - \sum_{i=1}^{C} y_{i} \log(p(\hat{y}_{i}))

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Truth: Class = 0

True class

Predicted probability

import flax.linen as nn

class MLP(nn.Module):
    @nn.compact
    def __call__(self, x):
      	# Linear
        x = nn.Dense(features=64)(x)
        # Non-linearity
        x = nn.silu(x)
        # Linear
        x = nn.Dense(features=64)(x)
        # Non-linearity
        x = nn.silu(x)
        # Linear
        x = nn.Dense(features=2)(x)
        return x

model = MLP()

Jax Models

import jax.numpy as jnp

example_input = jnp.ones((1,4))
params = model.init(jax.random.PRNGKey(0), example_input)

y = model.apply(params, example_input)

Architecture

Parameters

Call

p(x)

p(y|x)

p(x|y) = \frac{p(y|x)p(x)}{p(y)}

p(x|y)

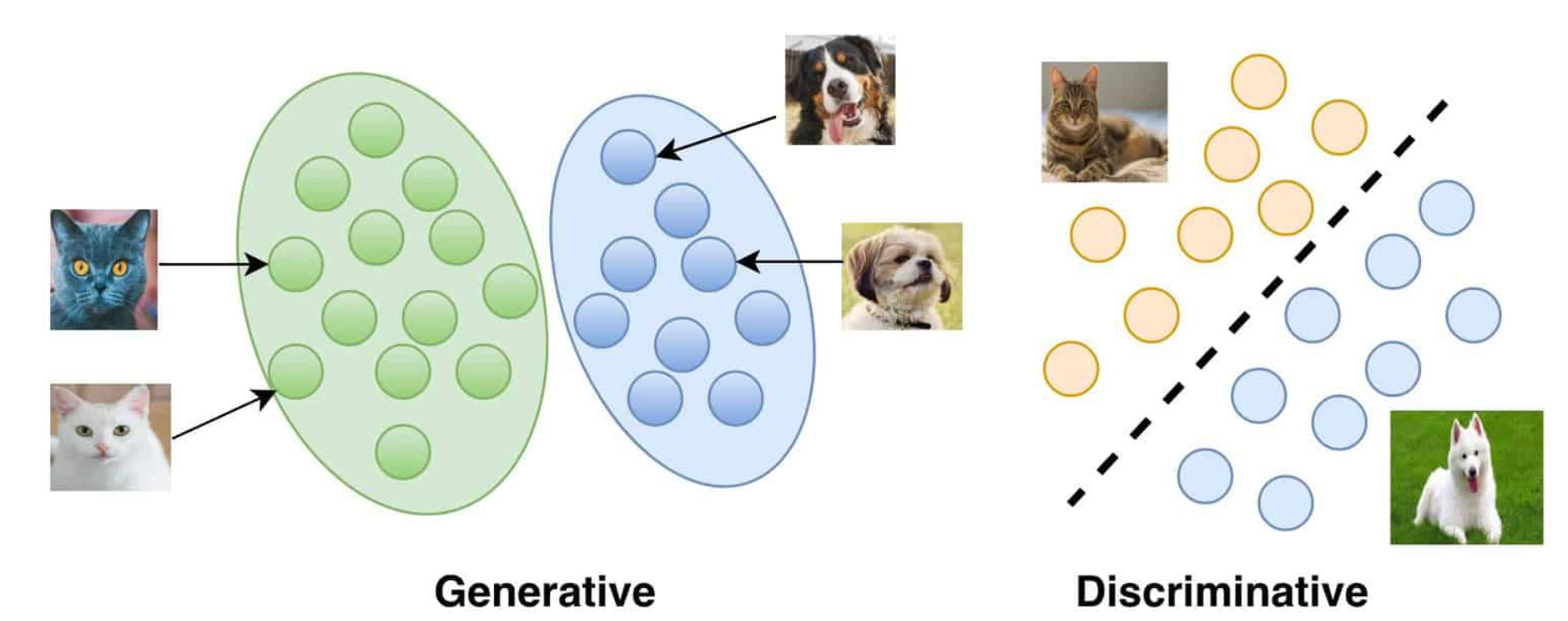
Generation vs Discrimination

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

p_\phi(x)

Data

A PDF that we can optimize

Maximize the likelihood of the data

Generative Models

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Generative Models 101

Maximize the likelihood of the training samples

\hat \phi = \argmax \left[ \log p_\phi (x_\mathrm{train}) \right]

x_1

x_2

Parametric Model

p_\phi(x)

Training Samples

x_\mathrm{train}

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

x_1

x_2

Trained Model

p_\phi(x)

Evaluate probabilities

Low Probability

High Probability

Generate Novel Samples

Simulator

Generative Model

Simulator

Generative Models: Simulate and Analyze

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

The Generative Zoo

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

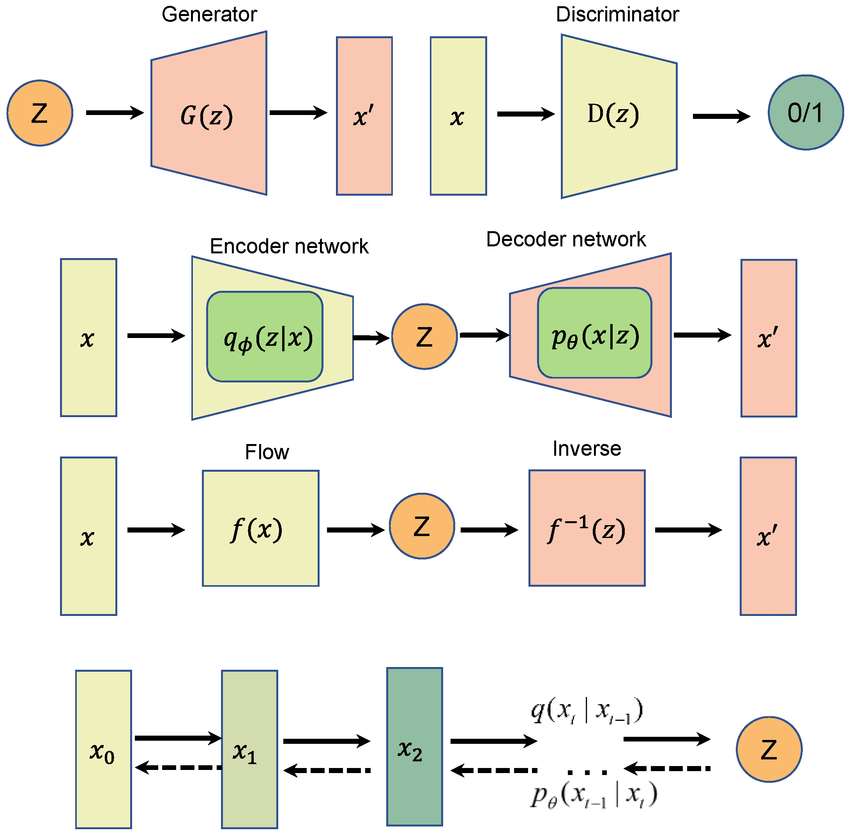
GANS

VAEs

Normalizing

Flows

Diffusion Models

[Image Credit: https://lilianweng.github.io/posts/2018-10-13-flow-models/]

Bridging two distributions

x_1

x_0

Base

Data

How is the bridge constrained?

Normalizing flows: Reverse = Forward inverse

Diffusion: Forward = Gaussian noising

Flow Matching: Forward = Interpolant

is p(x0) restricted?

Diffusion: p(x0) is Gaussian

Normalising flows: p(x0) can be evaluated

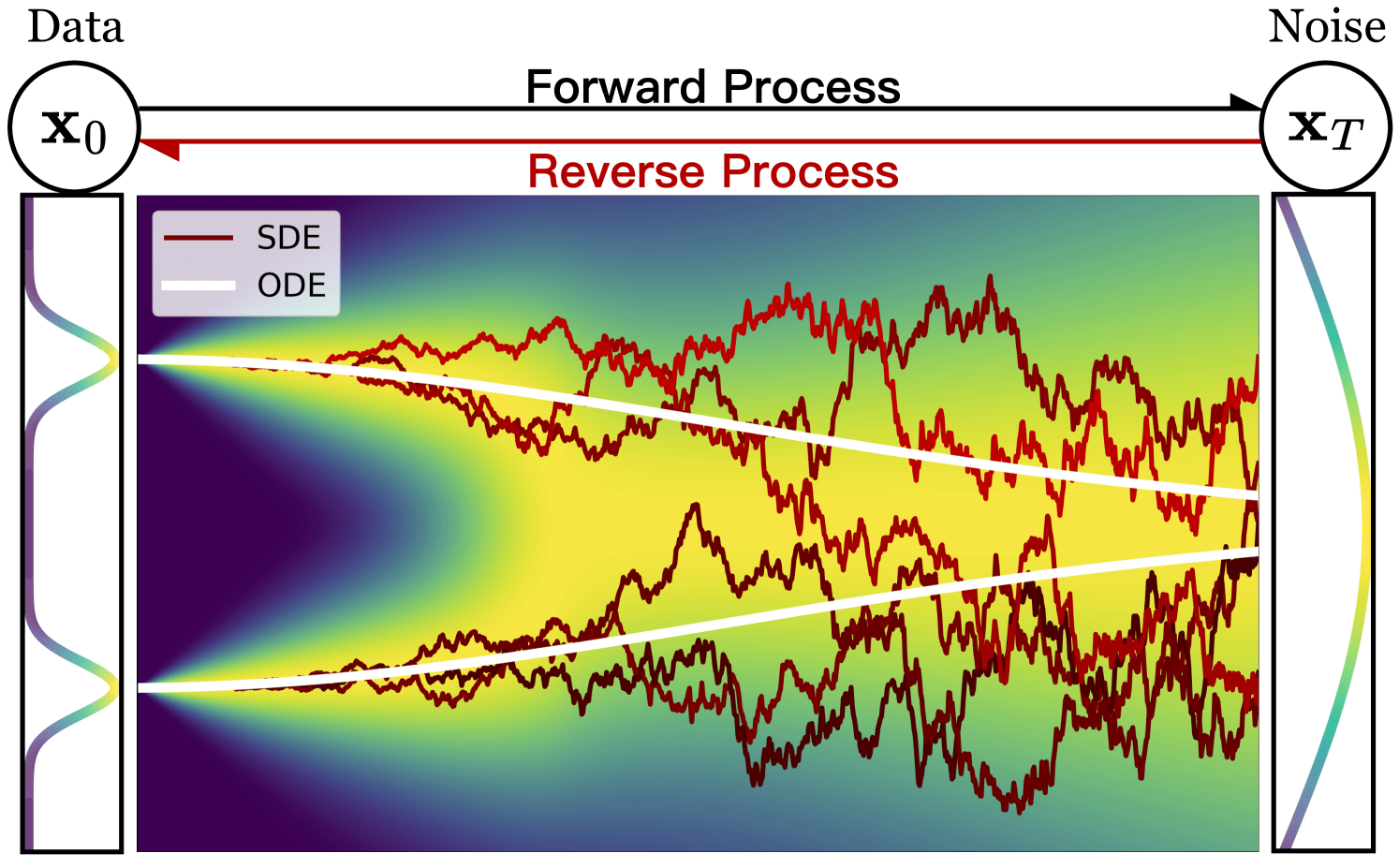
Is bridge stochastic (SDE) or deterministic (ODE)?

Diffusion: Stochastic (SDE)

Normalising flows: Deterministic (ODE)

Change of variables

X \sim \mathcal{N}(0,1)

sampled from a Gaussian distribution with mean 0 and variance 1

Y = g(X) = a X + b

How is

distributed?

p_Y(y) = p_X(g^{-1}(y)) \left| \frac{dg^{-1}(y)}{dy}\right|

P(Y\le y) = P(g(X)\le y) = P(X\le g^{-1}(y))

\mathrm{CDF}_Y = \mathrm{CDF}_{X}(g^{-1}(y))

Base distribution

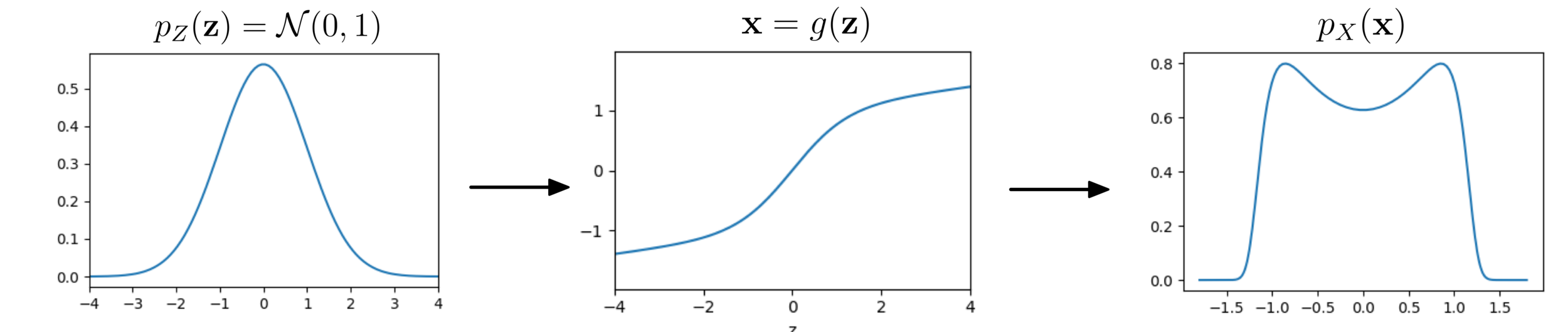
Target distribution

p_X(x) = p_Z(z) \left| \frac{dz}{dx}\right|

Z \sim \mathcal{N} (0,1) \rightarrow g(z) \rightarrow X

Invertible transformation

z \sim p_Z(z)

p_Z(z)

Normalizing flows

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

\mathrm{Uniform(0,1)} \rightarrow U_1, U_2

Z_0 = \sqrt{-2 \ln U_1} \cos(2 \pi U_2)

Z_1 = \sqrt{-2 \ln U_1} \sin(2 \pi U_2)

Z_0, Z_2 \leftarrow N(0,1)

Box-Muller transform

Normalizing flows in 1934

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Normalizing flows

[Image Credit: "Understanding Deep Learning" Simon J.D. Prince]

z \sim p(z)

x \sim p(x)

x = f(z)

p(x) = p(z = f^{-1}(x)) \left| \det J_{f^{-1}}(x) \right|

Bijective

Sample

Evaluate probabilities

Probability mass conserved locally

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

z_0 \sim p(z)

z_k = f_k(z_{k-1})

\log p(x) = \log p(z_0) - \sum_{k=1}^{K} \log \left| \det J_{f_k} (z_{k-1}) \right|

Image Credit: "Understanding Deep Learning" Simon J.D. Prince

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

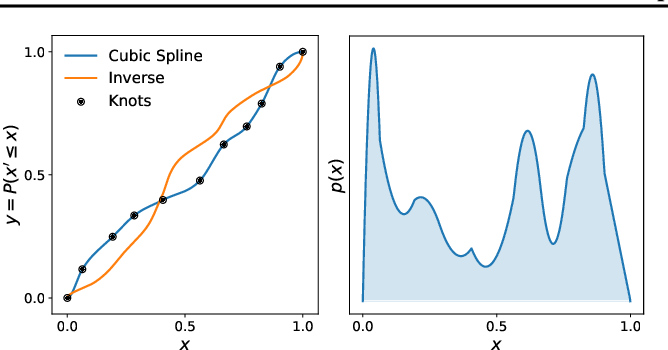
Invertible functions aren't that common!

Splines

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Issues NFs: Lack of flexibility

Invertible functions
Tractable Jacobians

Masked Autoregressive Flows

p(x) = \prod_i{p(x_i \,|\, x_{1:i-1})}

p(x_i \,|\, x_{1:i-1}) = \mathcal{N}(x_i \,|\,\mu_i, (\exp\alpha_i)^2)

\mu_i, \alpha_i = f_{\phi_i}(x_{1:i-1})

Neural Network

x_i = z_i \exp(\alpha_i) + \mu_i

z_i = (x_i - \mu_i) \exp(-\alpha_i)

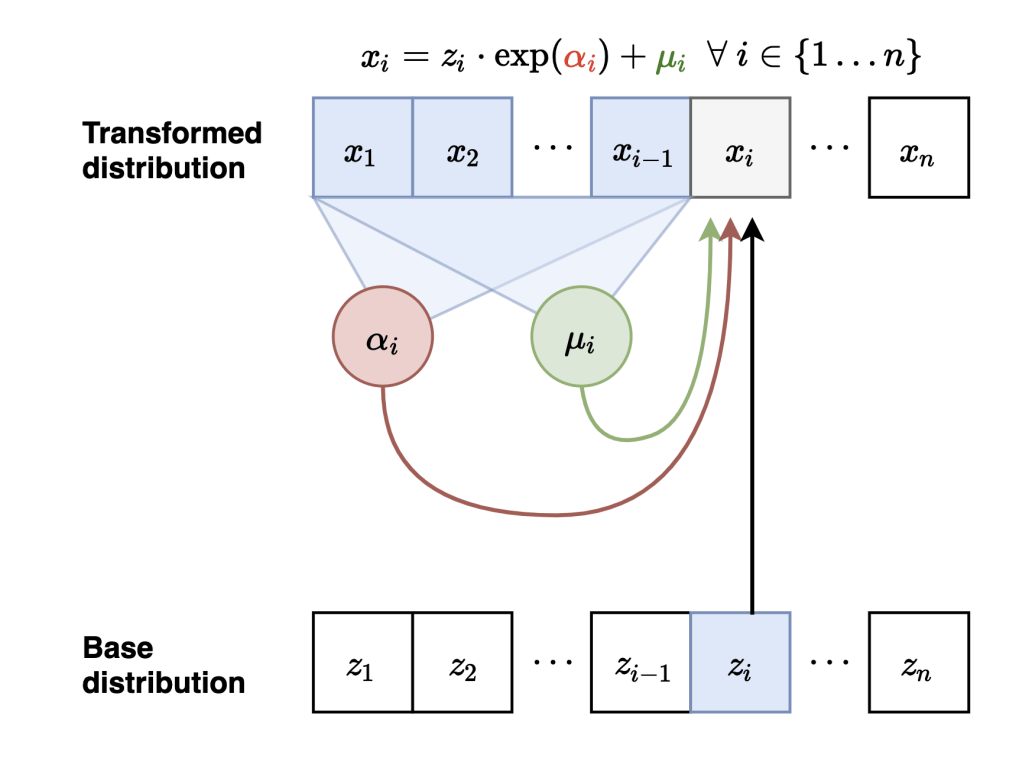
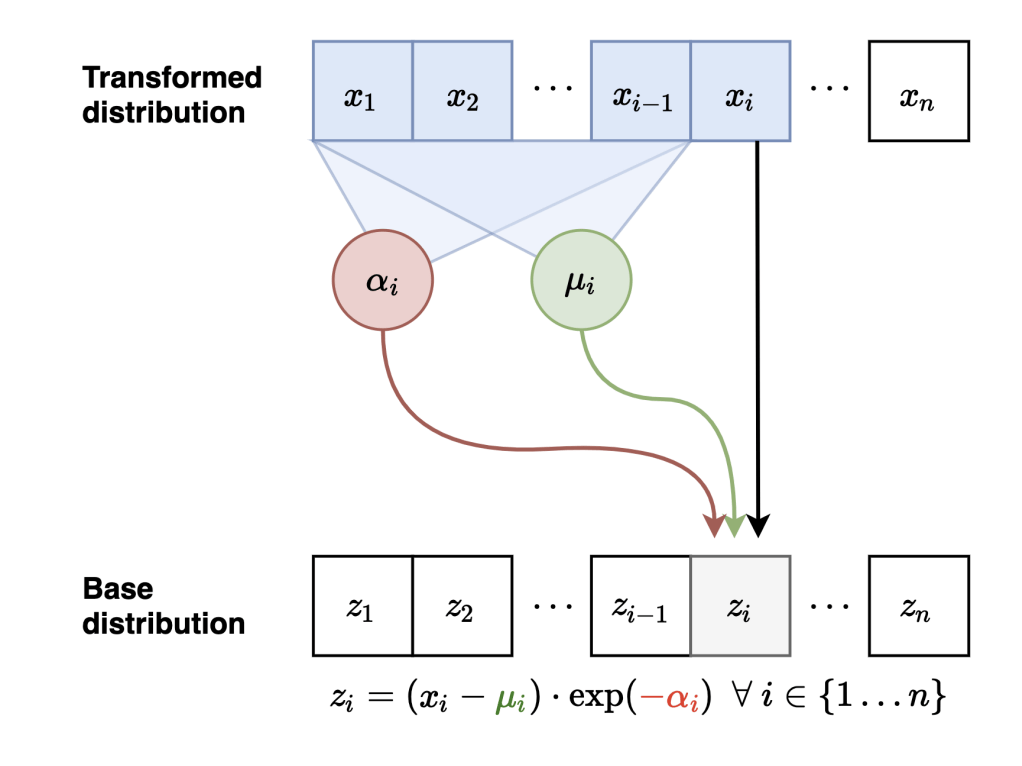
Sample

Evaluate probabilities

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

\theta

Forward Model

Observable

\color{darkgray}{\Omega_m}, \color{darkgreen}{w_0, w_a},\color{purple}{f_\mathrm{NL}}\, ...

Dark matter

Dark energy

Inflation

Predict

Infer

Parameters

Inverse mapping

\color{darkgray}{\sigma}, \color{darkgreen}{v}, ...

Fault line stress

Plate velocity

p(\theta|x)

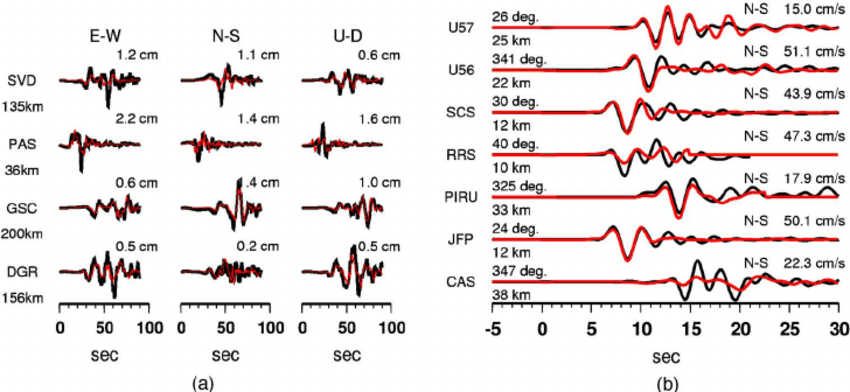
Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

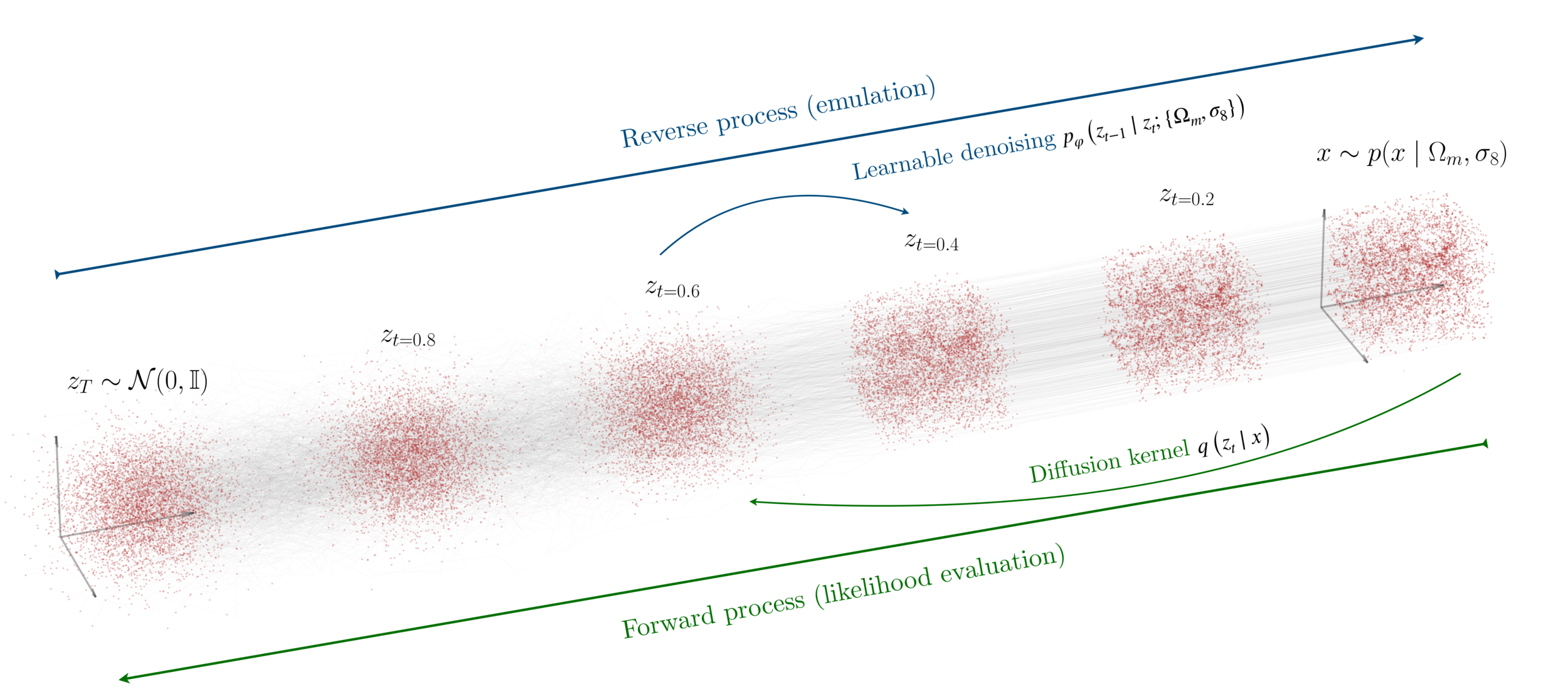
Simulation-based Inference

Normalizing flow

\frac{dx_t}{dt} = v^\phi_t(x_t)

x_1 = x_0 + \int_0^1 v^\phi_t(x_t) dt

\frac{d p(x_t)}{dt} = - \nabla \left( v^\phi_t(x_t) p(x_t) \right)

In continuous time

Continuity Equation

[Image Credit: "Understanding Deep Learning" Simon J.D. Prince]

x_0 = x_1 + \int_1^0 v^\phi_t(x_t) dt

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Chen et al. (2018), Grathwohl et al. (2018)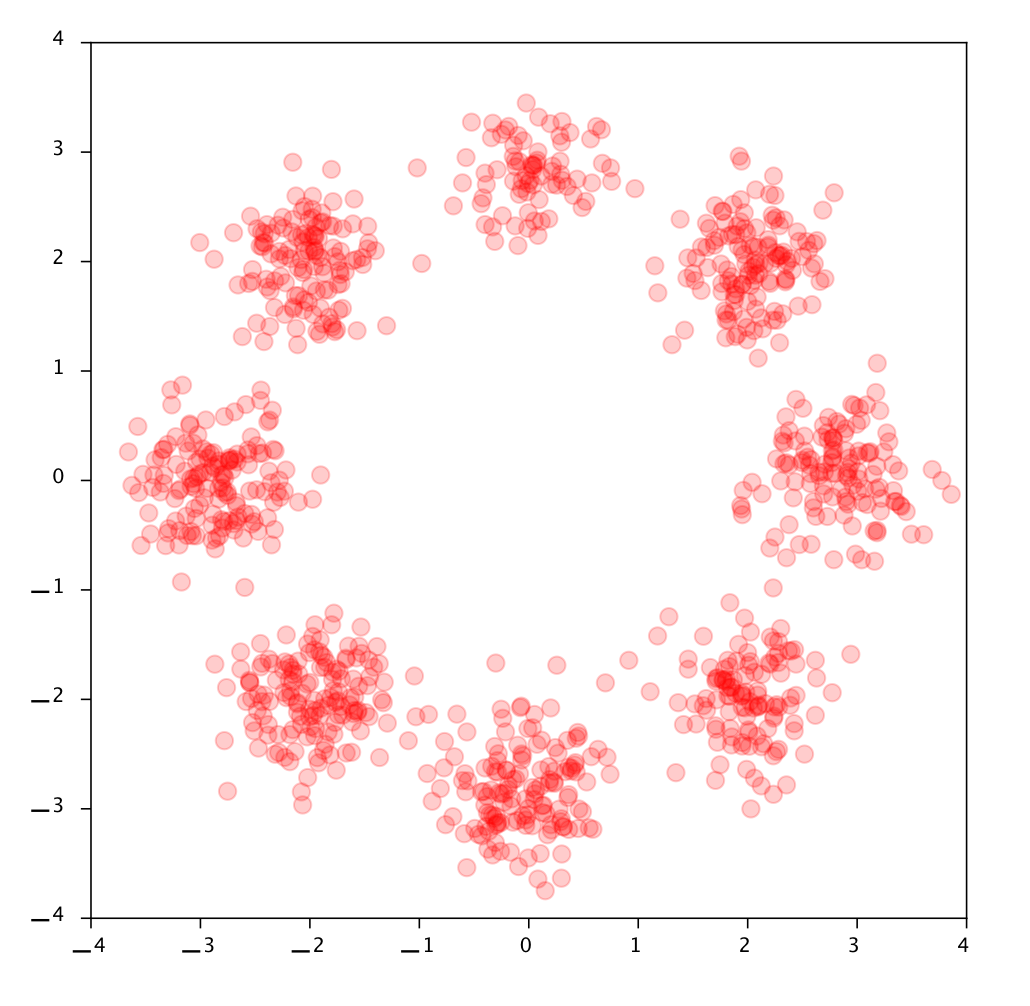

x_1 = x_0 + \int_0^1 v_\theta (x(t),t) dt

Generate

x_0

x_1

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Evaluate Probability

\log p_X(x) = \log p_Z(z) + \int_0^1 \mathrm{Tr} J_v (x(t)) dt

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Loss requires solving an ODE!

Diffusion, Flow matching, Interpolants... All ways to avoid this at training time

Conditional Flow matching

x_t = (1-t) x_0 + t x_1

\mathcal{L}_\mathrm{conditional} = \mathbb{E}_{t,x_0,x_1}\left[\| u_t^\phi(x_t) - u_t(x_0,x_1) \|^2 \right]

Assume a conditional vector field (known at training time)

The loss that we can compute

The gradients of the losses are the same!

\nabla_\phi \mathcal{L}_\mathrm{conditional} = \nabla_\phi \mathcal{L}

x_0

x_1

["Flow Matching for Generative Modeling" Lipman et al]

["Stochastic Interpolants: A Unifying framework for Flows and Diffusions" Albergo et al]

u_t(x) = \int u_t(x|x_1) \frac{p_t(x|x_1) p_1(x_1)}{p_t(x)} \, dx_1

p_t(x) = \int p_t(x|x_1) q(x_1) \, dx_1

Intractable

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Flow Matching

\frac{dz_t}{dt} = u^\phi_t(z_t)

x = z_0 + \int_0^1 u^\phi_t(z_t) dt

Continuity equation

\frac{d p(z_t)}{dt} = - \nabla \left( u^\phi_t(z_t) p(z_t) \right)

[Image Credit: "Understanding Deep Learning" Simon J.D. Prince]

Sample

Evaluate probabilities

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

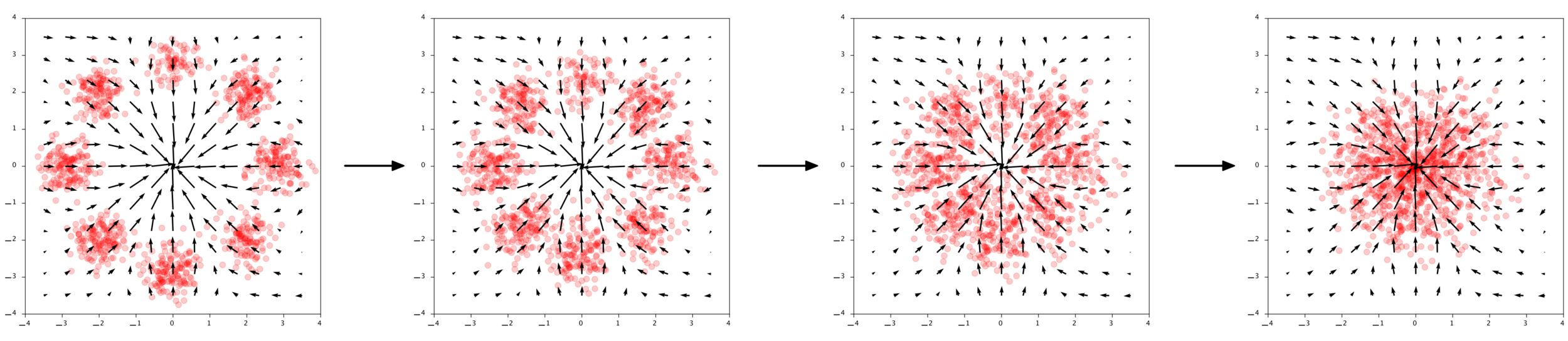
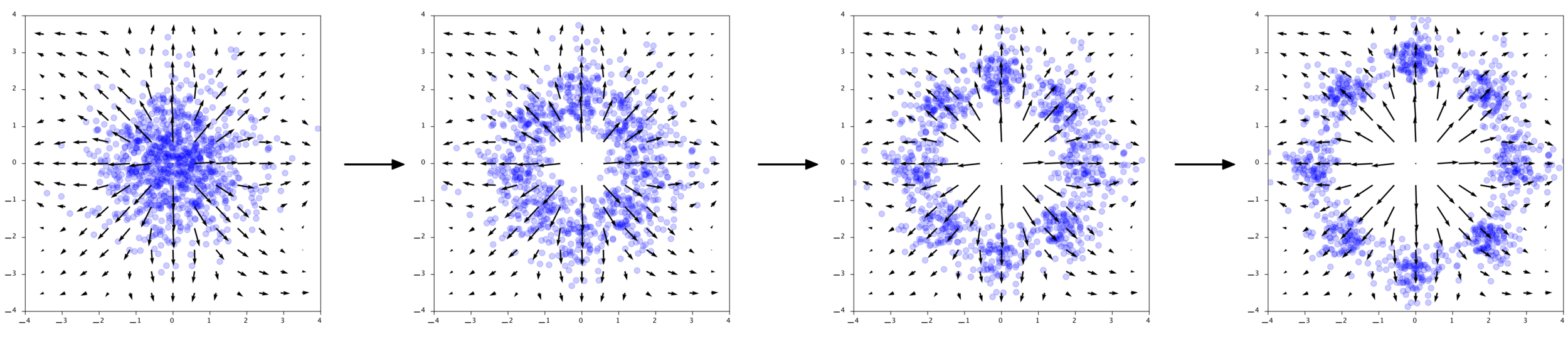
Diffusion Models

Reverse diffusion: Denoise previous step

Forward diffusion: Add Gaussian noise (fixed)

Prompt

A person half Yoda half Gandalf

Denoising = Regression

Fixed base distribution:

Gaussian

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

["A point cloud approach to generative modeling for galaxy surveys at the field level"

Cuesta-Lazaro and Mishra-Sharma
International Conference on Machine Learning ICML AI4Astro 2023, Spotlight talk, arXiv:2311.17141]

Base Distribution

Target Distribution

Simulated Galaxy 3d Map

Prompt:

\Omega_m, \sigma_8

Prompt: A person half Yoda half Gandalf

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Tutorial 2

x_0

Gaussian

MNIST

x_1

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Students at MIT are

Pre-trained on next word prediction

...

OVER-CAFFEINATED

NERDS

SMART

ATHLETIC

Large Language Models

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

https://www.astralcodexten.com/p/janus-simulators

How do we encode "helpful" in the loss function?

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Step 1

Human teaches desired output

Explain RLHF

After training the model...

Step 2

Human scores outputs

+ teaches Reward model to score

it is the method by which ...

Explain means to tell someone...

Explain RLHF

Step 3

Tune the Language Model to produce high rewards!

RLHF: Reinforcement Learning from Human Feedback

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

BEFORE RLHF

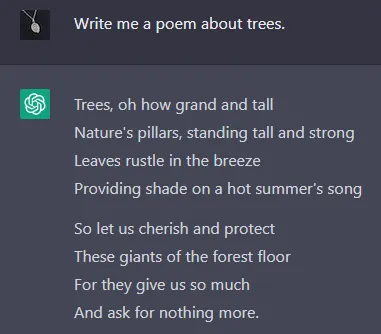
AFTER RLHF

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Reasoning

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Reasoning

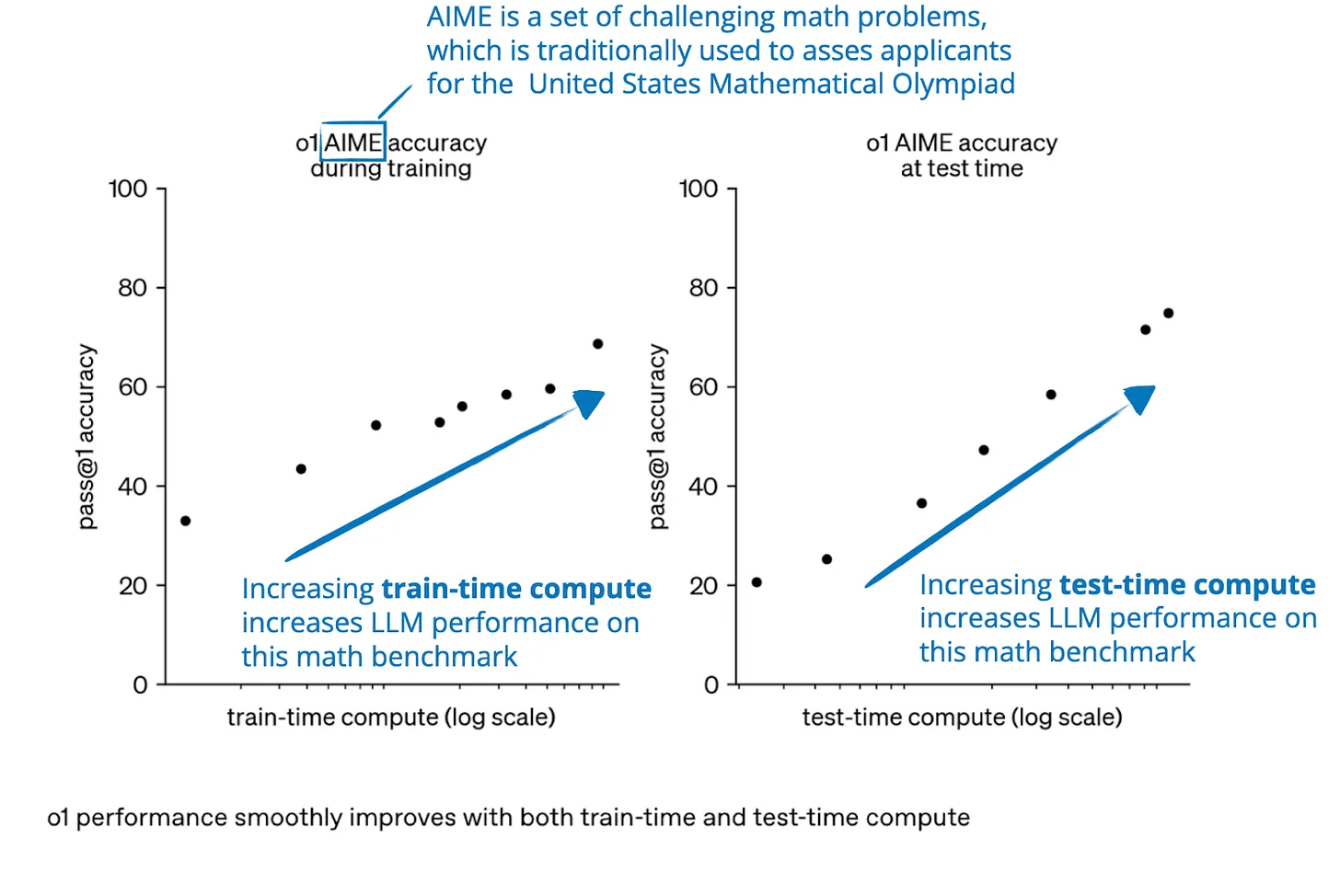
Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

RLVR (Verifiable Rewards)

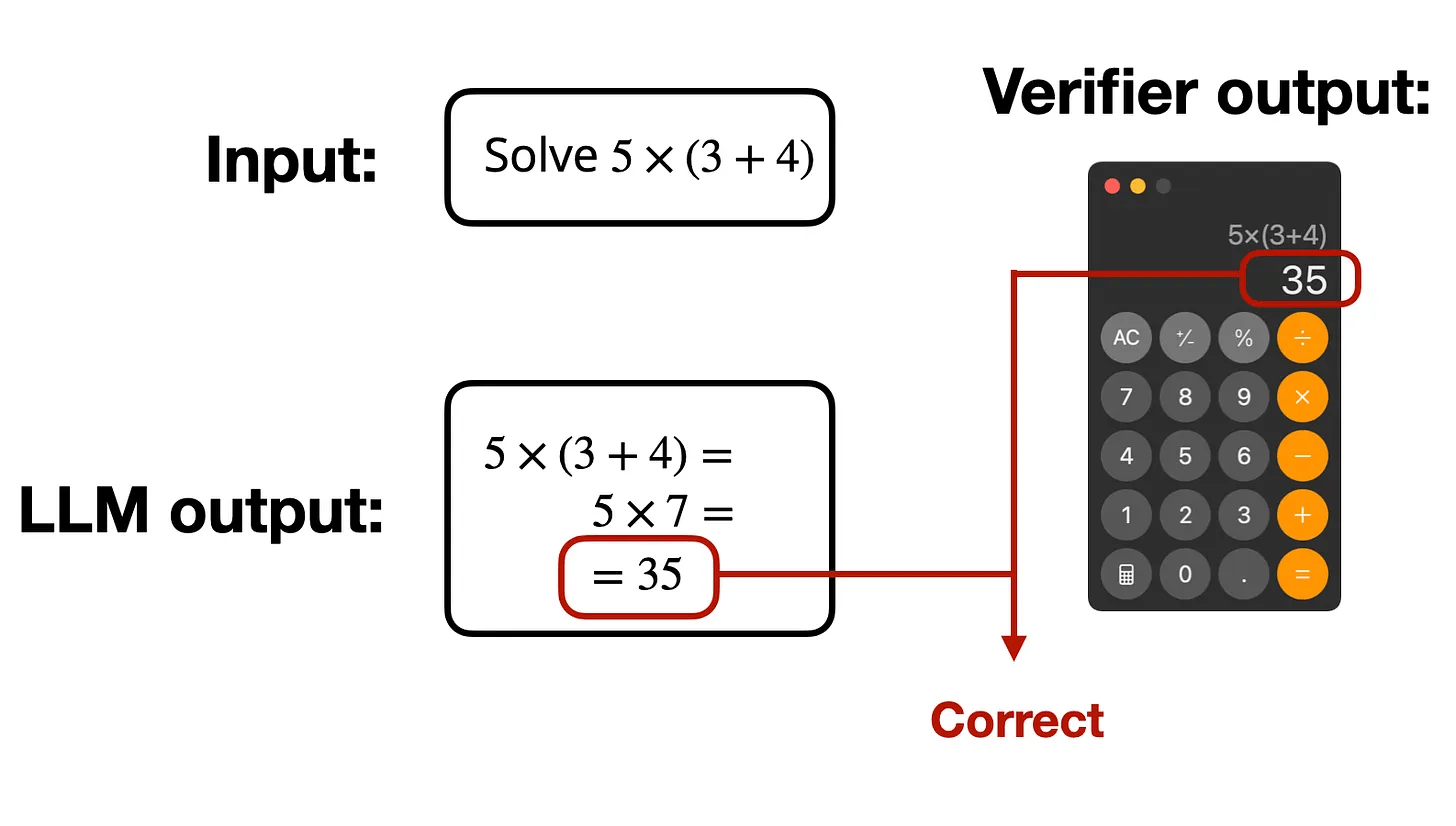
Examples: Code execution, game playing, instruction following ....

[Image Credit: AgentBench https://arxiv.org/abs/2308.03688]

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Agents

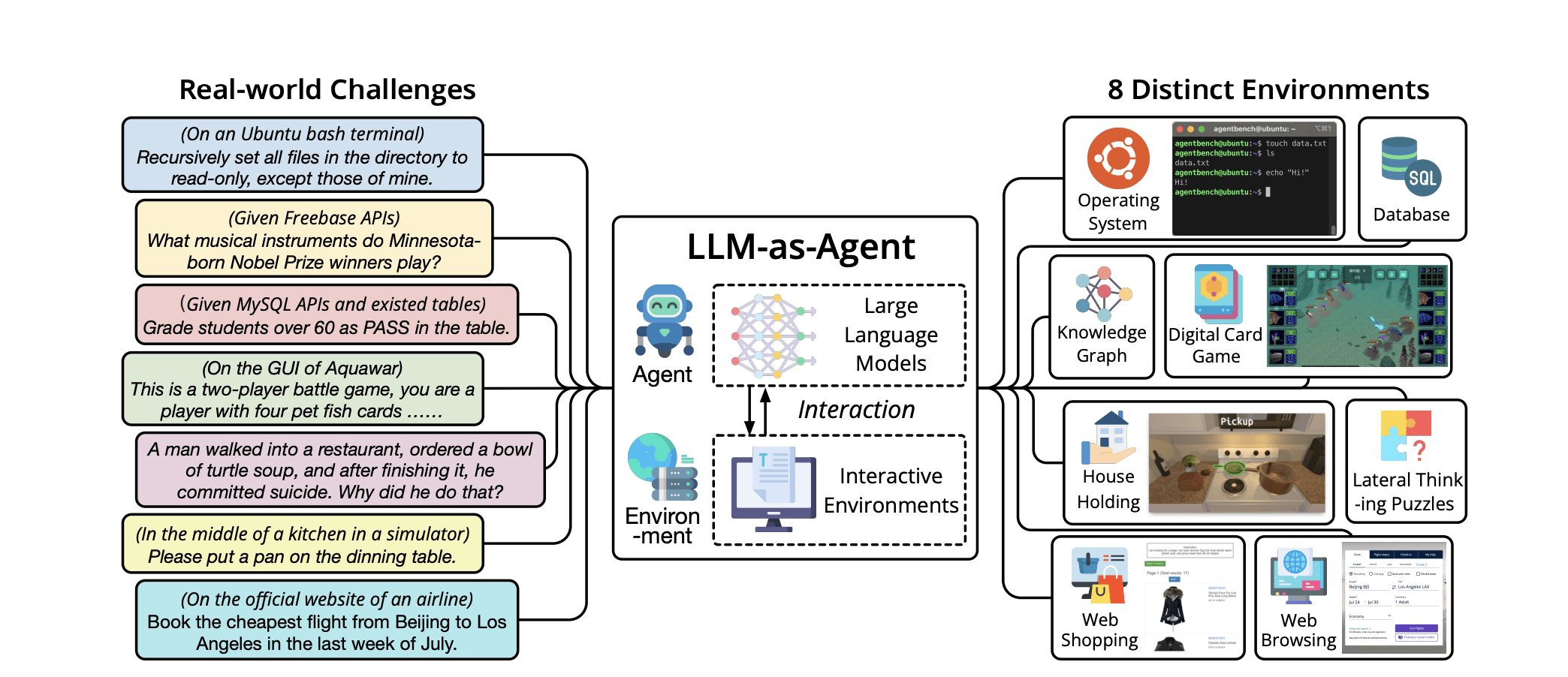
Books by Kevin P. Murphy
- Machine learning, a probabilistic perspective
- Probabilistic Machine Learning: advanced topics
ML4Astro workshop https://ml4astro.github.io/icml2023/
ProbAI summer school https://github.com/probabilisticai/probai-2023
IAIFI Summer school
- https://github.com/iaifi/summer-school-2023
- Tutorials https://github.com/florpi/summer_school_generative
Blogposts

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

References

cuestalz@mit.edu