From Zero to Generative

IAIFI Fellow, MIT

Carolina Cuesta-Lazaro

Art: "The art of painting" by Johannes Vermeer

Learning Generative Modelling from scratch

p(\mathrm{World}|\mathrm{Prompt})
["Genie 2: A large-scale foundation model" Parker-Holder et al]
p(\mathrm{Drug}|\mathrm{Properties})
["Generative AI for designing and validating easily synthesizable and structurally novel antibiotics" Swanson et al]

Probabilistic ML has made high dimensional inference tractable

1024x1024xTime

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

https://parti.research.google​​​​​​​

A portrait photo of  a kangaroo wearing an orange hoodie and blue sunglasses standing on the grass in front of the Sydney Opera House holding a sign on the chest that says Welcome Friends!

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

BEFORE

Artificial General Intelligence?

AFTER

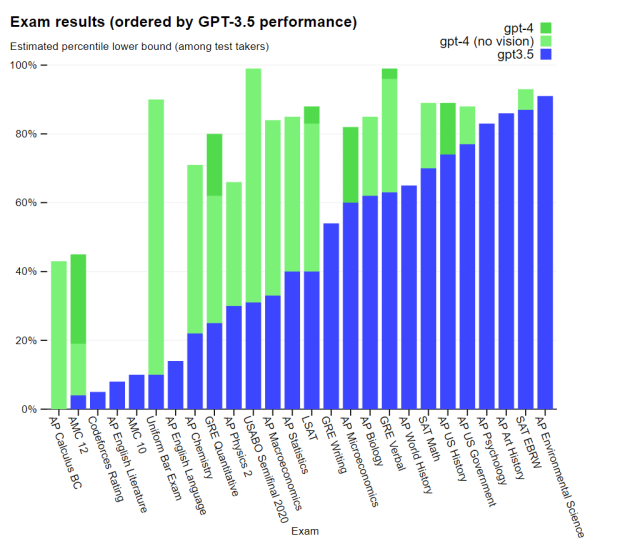
Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

p(x)
p(y|x)
p(x|y) = \frac{p(y|x)p(x)}{p(y)}
p(x|y)

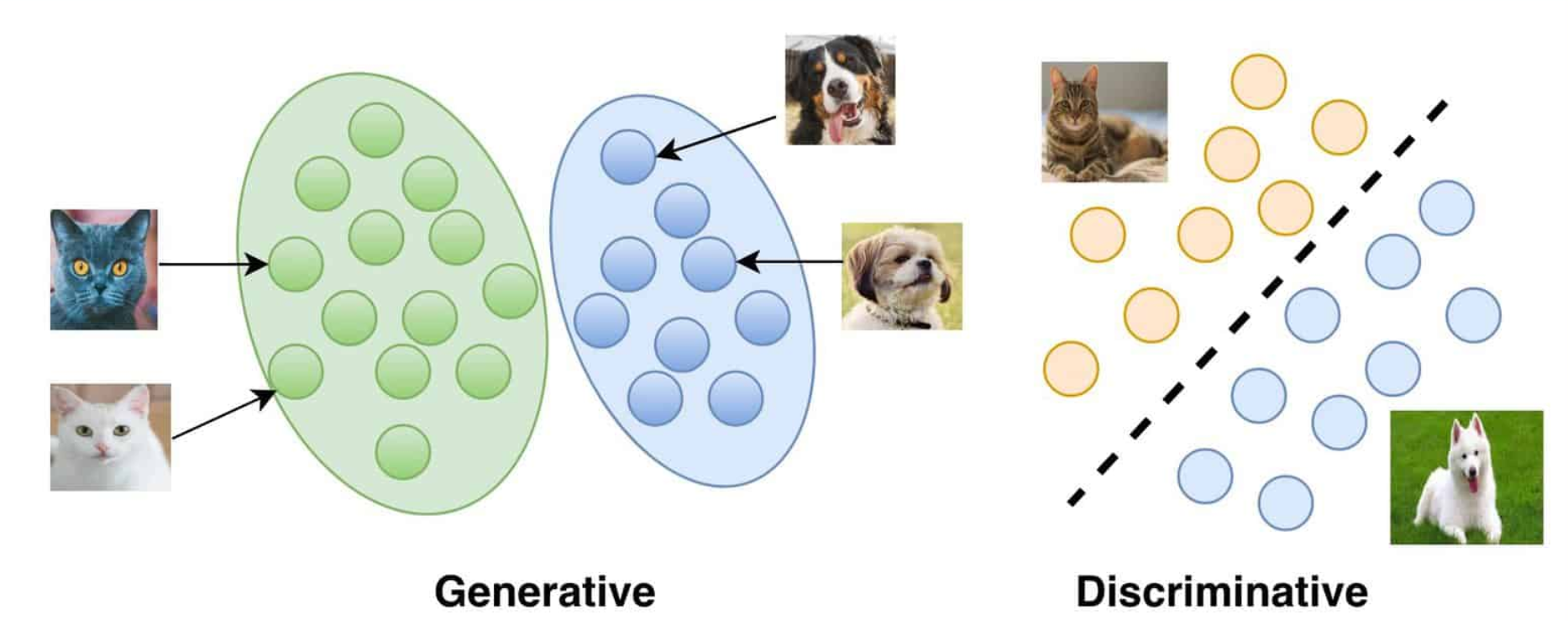
Generation vs Discrimination

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

p_\phi(x)

Data

A PDF that we can optimize

Maximize the likelihood of the data

Generative Models

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Generative Models 101

Maximize the likelihood of the training samples

\hat \phi = \argmax \left[ \log p_\phi (x_\mathrm{train}) \right]
x_1
x_2

Parametric Model

p_\phi(x)

Training Samples

x_\mathrm{train}

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

x_1
x_2

Trained Model

p_\phi(x)

Evaluate probabilities

Low Probability

High Probability

Generate Novel Samples

Simulator

Generative Model

Generative Model

Simulator

Generative Models: Simulate and Analyze

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

The Generative Zoo

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

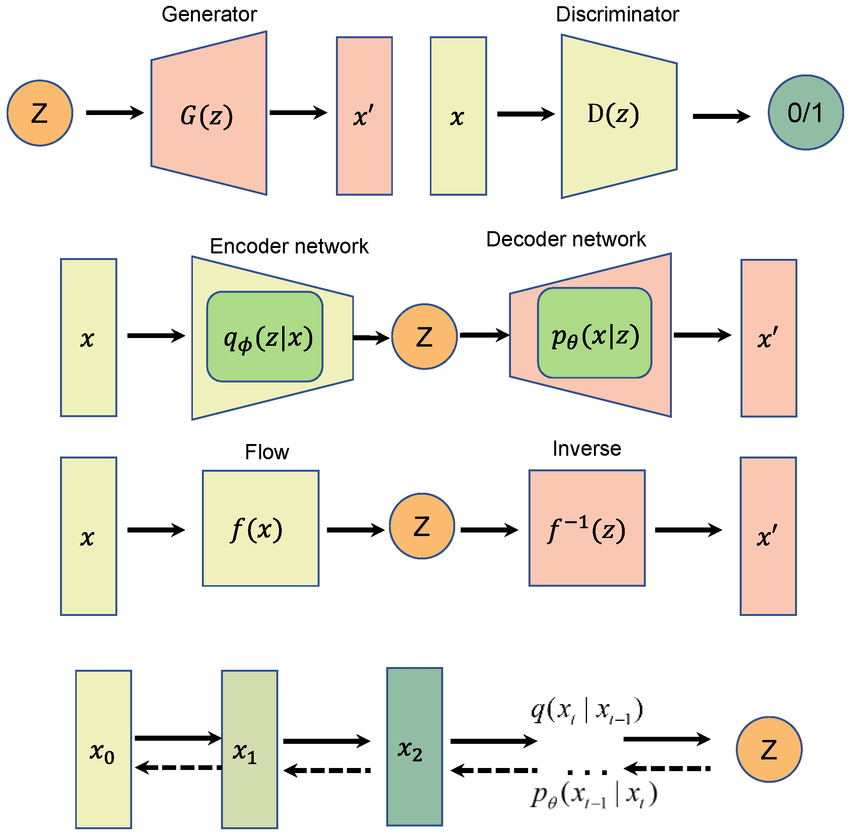
GANS

VAEs

Normalizing

Flows

Diffusion Models

[Image Credit: https://lilianweng.github.io/posts/2018-10-13-flow-models/]

Bridging two distributions

x_1
x_0

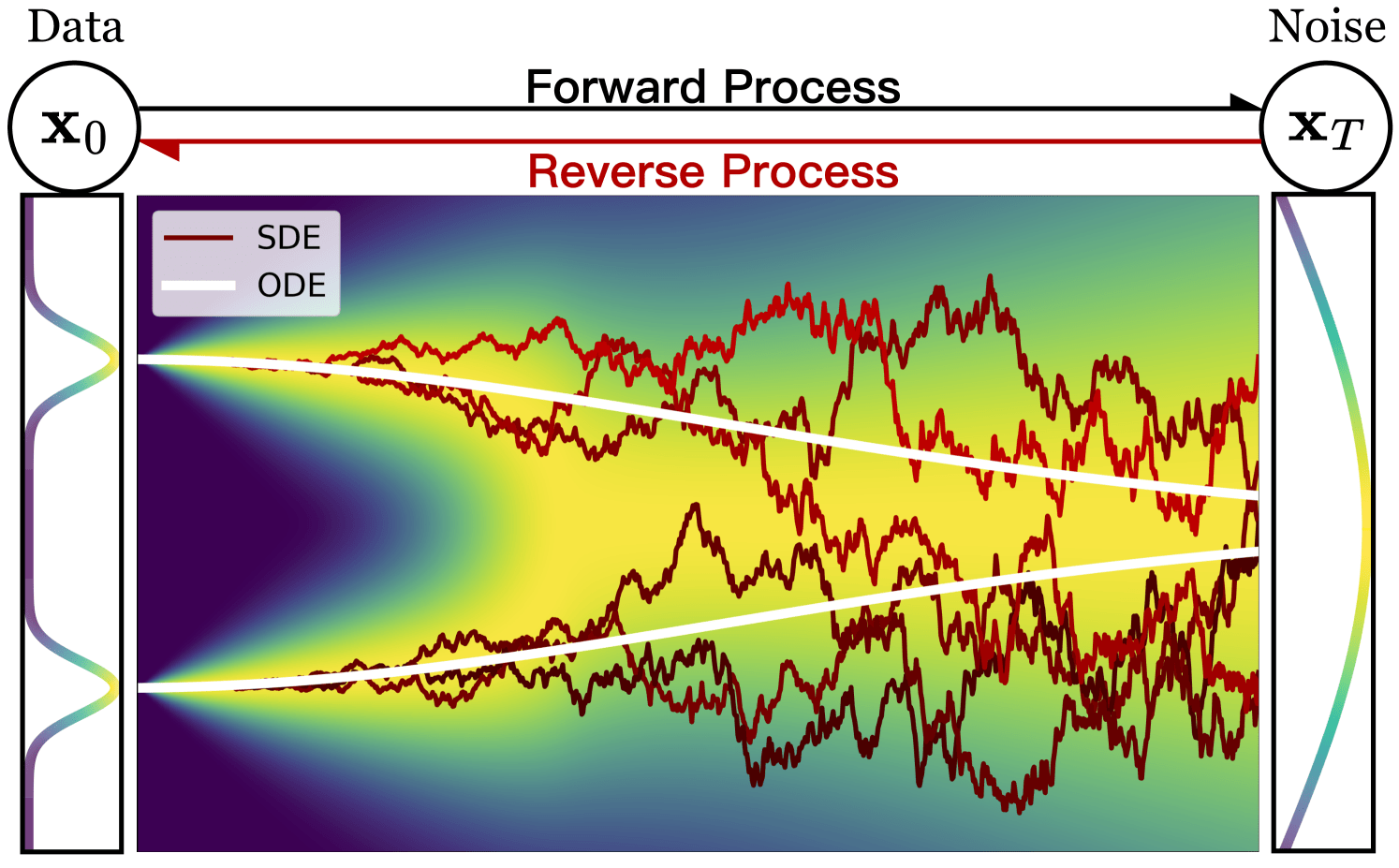
Base

Data

How is the bridge constrained?

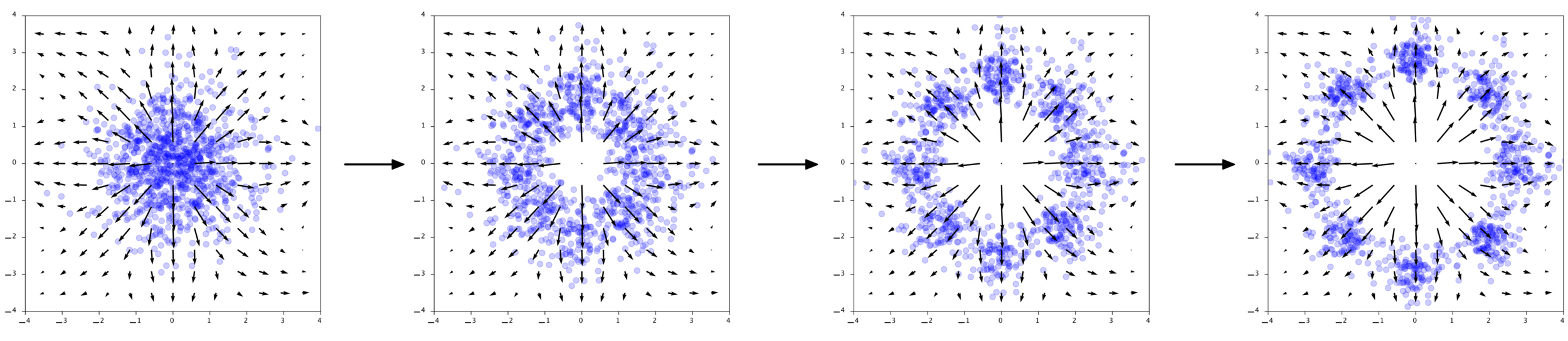
Normalizing flows: Reverse = Forward inverse

Diffusion: Forward = Gaussian noising

Flow Matching: Forward = Interpolant

is p(x0) restricted?

Diffusion: p(x0) is Gaussian

Normalising flows: p(x0) can be evaluated

Is bridge stochastic (SDE) or deterministic (ODE)?

Diffusion: Stochastic (SDE)

Normalising flows: Deterministic (ODE)

(Exact likelihood evaluation)

Change of variables

X \sim \mathcal{N}(0,1)

sampled from a Gaussian distribution with mean 0 and variance 1

Y = g(X) = a X + b

How is 

Y

distributed?

p_Y(y) = p_X(g^{-1}(y)) \left| \frac{dg^{-1}(y)}{dy}\right|
P(Y\le y) = P(g(X)\le y) = P(X\le g^{-1}(y))
\mathrm{CDF}_Y = \mathrm{CDF}_{X}(g^{-1}(y))

Base distribution

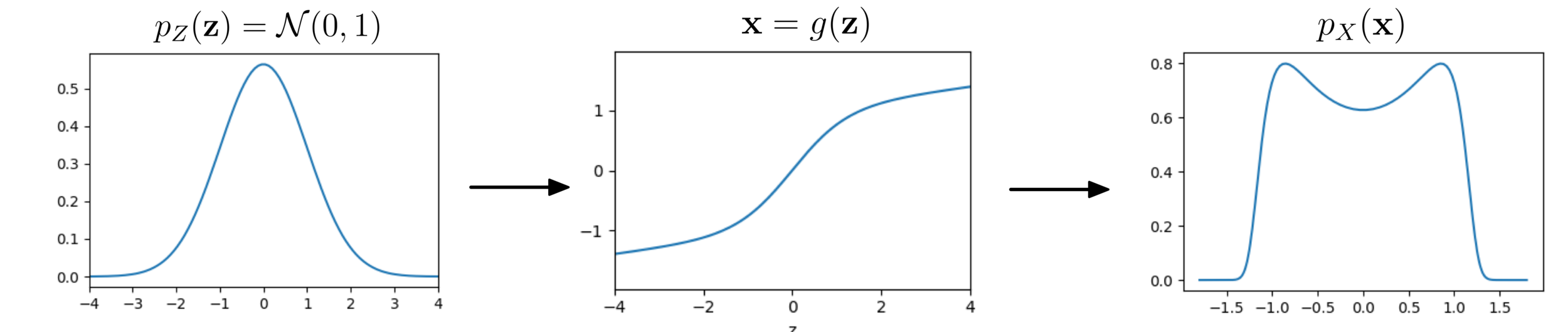
Target distribution

p_X(x) = p_Z(z) \left| \frac{dz}{dx}\right|
Z \sim \mathcal{N} (0,1) \rightarrow g(z) \rightarrow X

Invertible transformation

z \sim p_Z(z)
p_Z(z)

Normalizing flows

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

\mathrm{Uniform(0,1)} \rightarrow U_1, U_2
Z_0 = \sqrt{-2 \ln U_1} \cos(2 \pi U_2)
Z_1 = \sqrt{-2 \ln U_1} \sin(2 \pi U_2)
Z_0, Z_2 \leftarrow N(0,1)

Box-Muller transform

Normalizing flows in 1934

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Normalizing flows

[Image Credit: "Understanding Deep Learning" Simon J.D. Prince]
z \sim p(z)
x \sim p(x)
x = f(z)
p(x) = p(z = f^{-1}(x)) \left| \det J_{f^{-1}}(x) \right|

Bijective

Sample

Evaluate probabilities

Probability mass conserved locally

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

z_0 \sim p(z)
z_k = f_k(z_{k-1})
\log p(x) = \log p(z_0) - \sum_{k=1}^{K} \log \left| \det J_{f_k} (z_{k-1}) \right|
Image Credit: "Understanding Deep Learning" Simon J.D. Prince

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

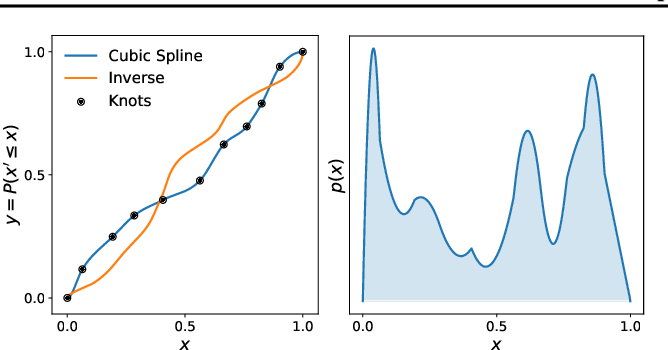
Invertible functions aren't that common!

Splines

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Issues NFs: Lack of flexibility

  • Invertible functions
  • Tractable Jacobians

 

Masked Autoregressive Flows

p(x) = \prod_i{p(x_i \,|\, x_{1:i-1})}
p(x_i \,|\, x_{1:i-1}) = \mathcal{N}(x_i \,|\,\mu_i, (\exp\alpha_i)^2)
\mu_i, \alpha_i = f_{\phi_i}(x_{1:i-1})

Neural Network

x_i = z_i \exp(\alpha_i) + \mu_i
z_i = (x_i - \mu_i) \exp(-\alpha_i)

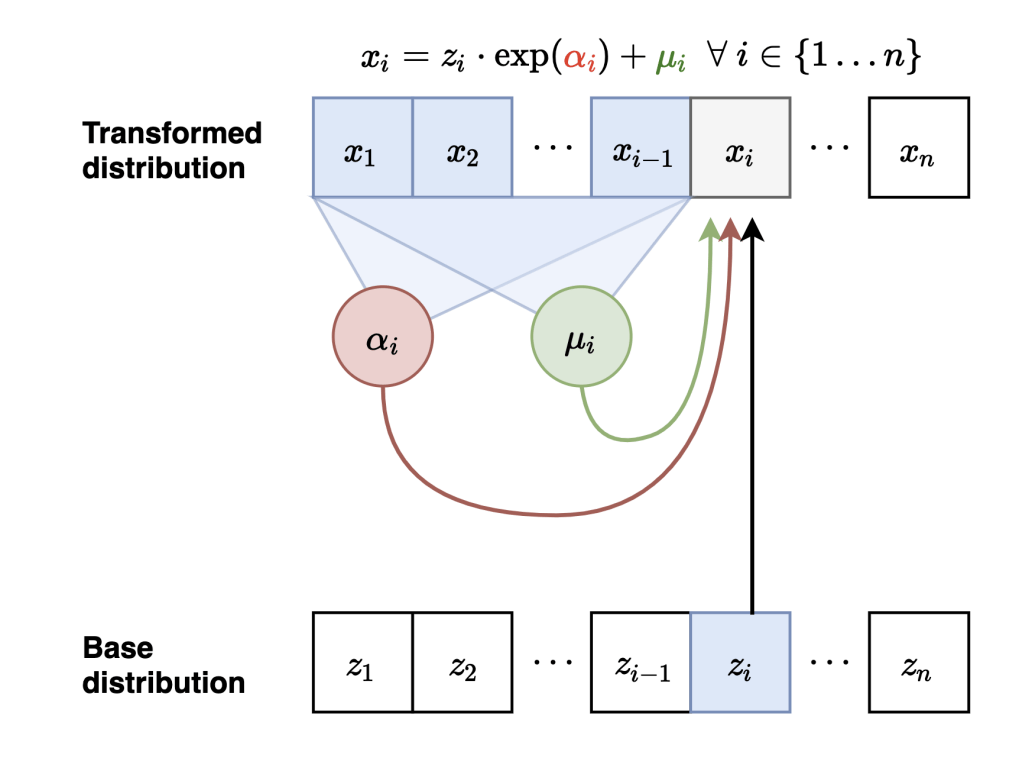
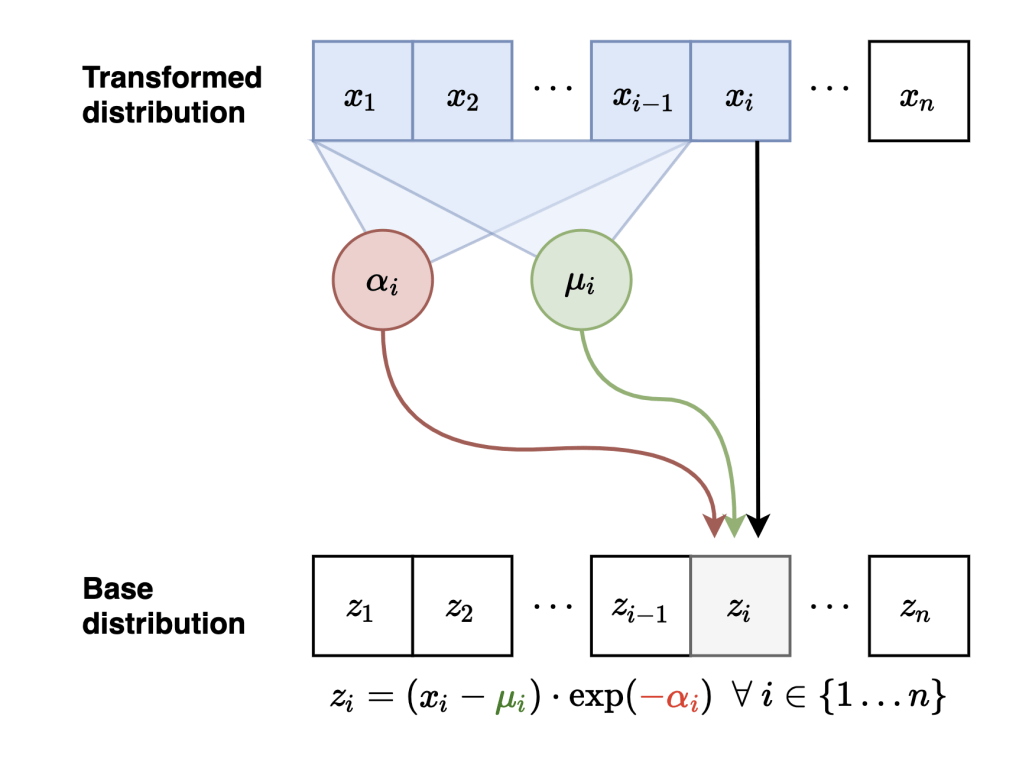
Sample

Evaluate probabilities

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

\theta

Forward Model

Observable

x
\color{darkgray}{\Omega_m}, \color{darkgreen}{w_0, w_a},\color{purple}{f_\mathrm{NL}}\, ...

Dark matter

Dark energy

Inflation

Predict

Infer

Parameters

Inverse mapping

\color{darkgray}{\sigma}, \color{darkgreen}{v}, ...

Fault line stress

Plate velocity

p(\theta|x)

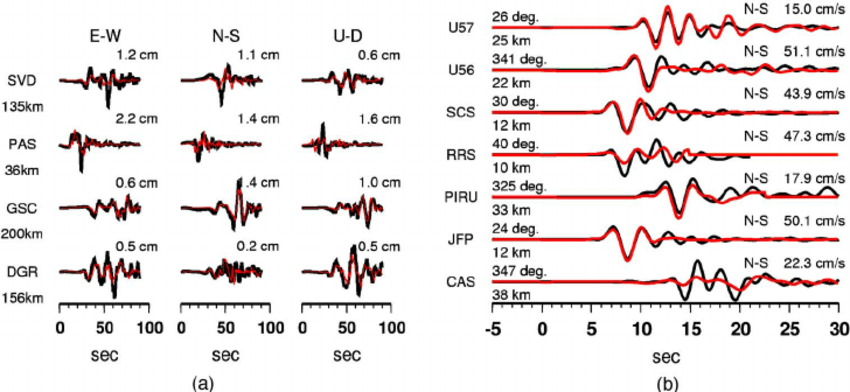
Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Simulation-based Inference

Normalizing flow

\frac{dx_t}{dt} = v^\phi_t(x_t)
x_1 = x_0 + \int_0^1 v^\phi_t(x_t) dt
\frac{d p(x_t)}{dt} = - \nabla \left( v^\phi_t(x_t) p(x_t) \right)

In continuous time

Continuity Equation

[Image Credit: "Understanding Deep Learning" Simon J.D. Prince]
x_0 = x_1 + \int_1^0 v^\phi_t(x_t) dt

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Chen et al. (2018), Grathwohl et al. (2018)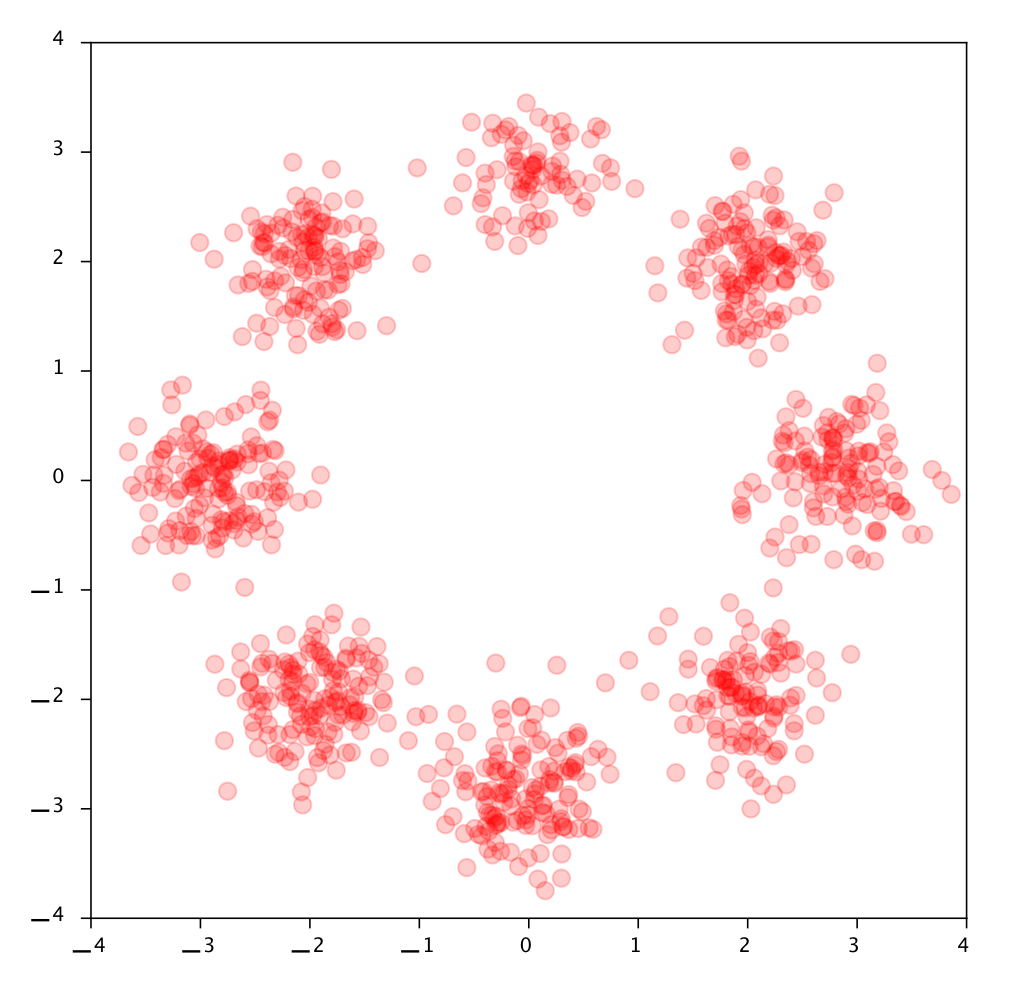
x_1 = x_0 + \int_0^1 v_\theta (x(t),t) dt

Generate

x_0
x_1

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

t

Evaluate Probability

\log p_X(x) = \log p_Z(z) + \int_0^1 \mathrm{Tr} J_v (x(t)) dt

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Loss requires solving an ODE!

Diffusion, Flow matching, Interpolants... All ways to avoid this at training time

Conditional Flow matching

x_t = (1-t) x_0 + t x_1
\mathcal{L}_\mathrm{conditional} = \mathbb{E}_{t,x_0,x_1}\left[\| u_t^\phi(x_t) - u_t(x_0,x_1) \|^2 \right]

Assume a conditional vector field (known at training time)

The loss that we can compute

The gradients of the losses are the same!

\nabla_\phi \mathcal{L}_\mathrm{conditional} = \nabla_\phi \mathcal{L}
x_0
x_1
["Flow Matching for Generative Modeling" Lipman et al]

["Stochastic Interpolants: A Unifying framework for Flows and Diffusions" Albergo et al]
u_t(x) = \int u_t(x|x_1) \frac{p_t(x|x_1) p_1(x_1)}{p_t(x)} \, dx_1
p_t(x) = \int p_t(x|x_1) q(x_1) \, dx_1

Intractable

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Flow Matching

\frac{dz_t}{dt} = u^\phi_t(z_t)
x = z_0 + \int_0^1 u^\phi_t(z_t) dt

Continuity equation

\frac{d p(z_t)}{dt} = - \nabla \left( u^\phi_t(z_t) p(z_t) \right)
[Image Credit: "Understanding Deep Learning" Simon J.D. Prince]

Sample

Evaluate probabilities

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

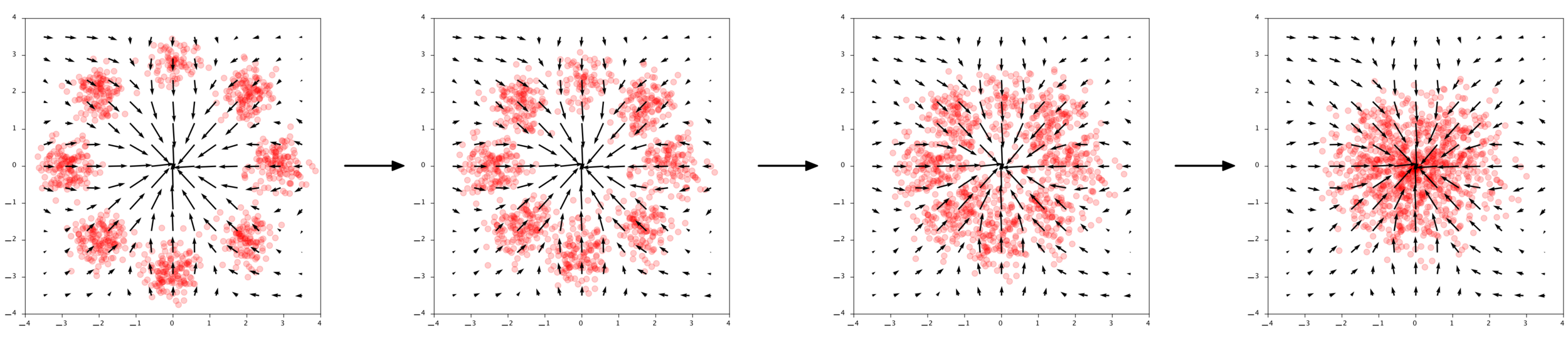
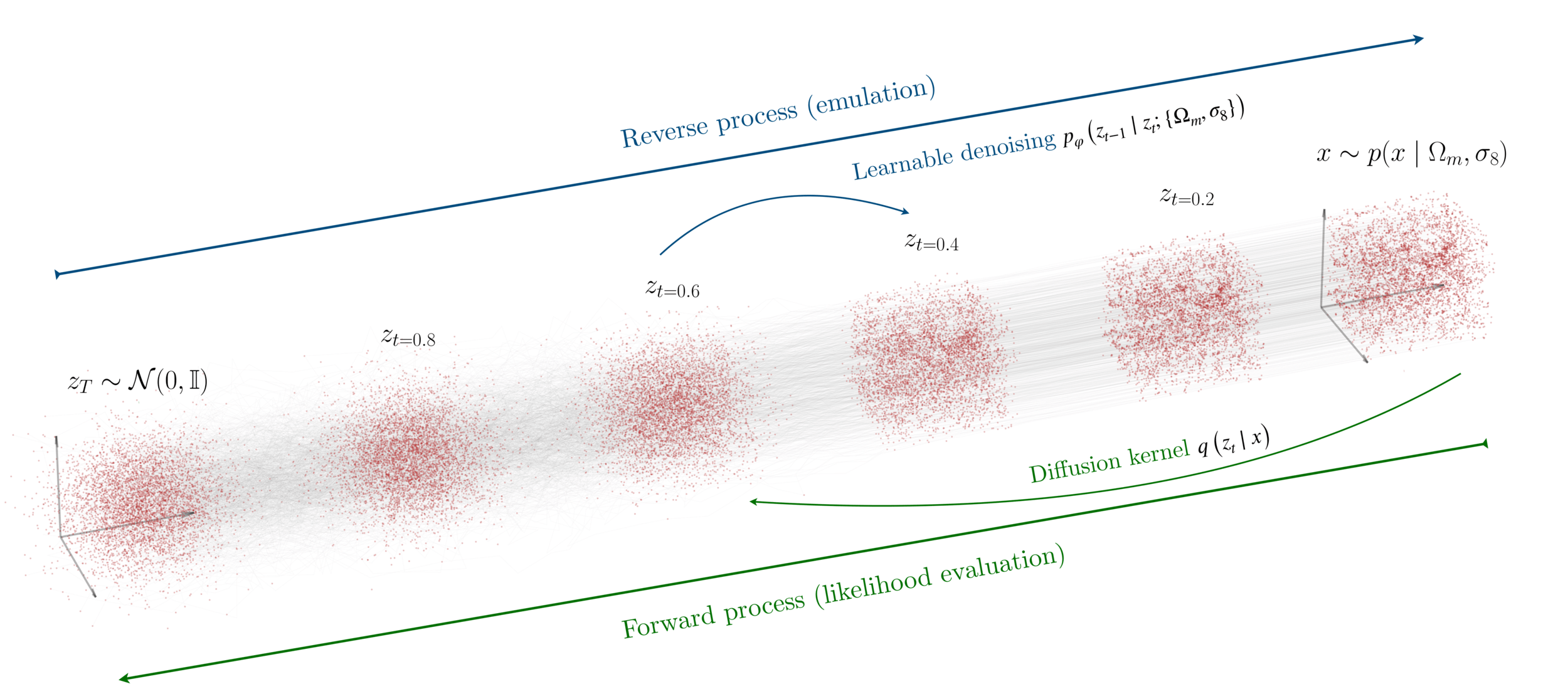
Diffusion Models

Reverse diffusion: Denoise previous step

Forward diffusion: Add Gaussian noise (fixed)

Prompt

A person half Yoda half Gandalf

Denoising = Regression

Fixed base distribution:

Gaussian

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

["A point cloud approach to generative modeling for galaxy surveys at the field level"

Cuesta-Lazaro and Mishra-Sharma
International Conference on Machine Learning ICML AI4Astro 2023, Spotlight talk, arXiv:2311.17141]

Base Distribution

Target Distribution

Simulated Galaxy 3d Map

Prompt:

\Omega_m, \sigma_8

Prompt: A person half Yoda half Gandalf

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Autoregressive in Frequency

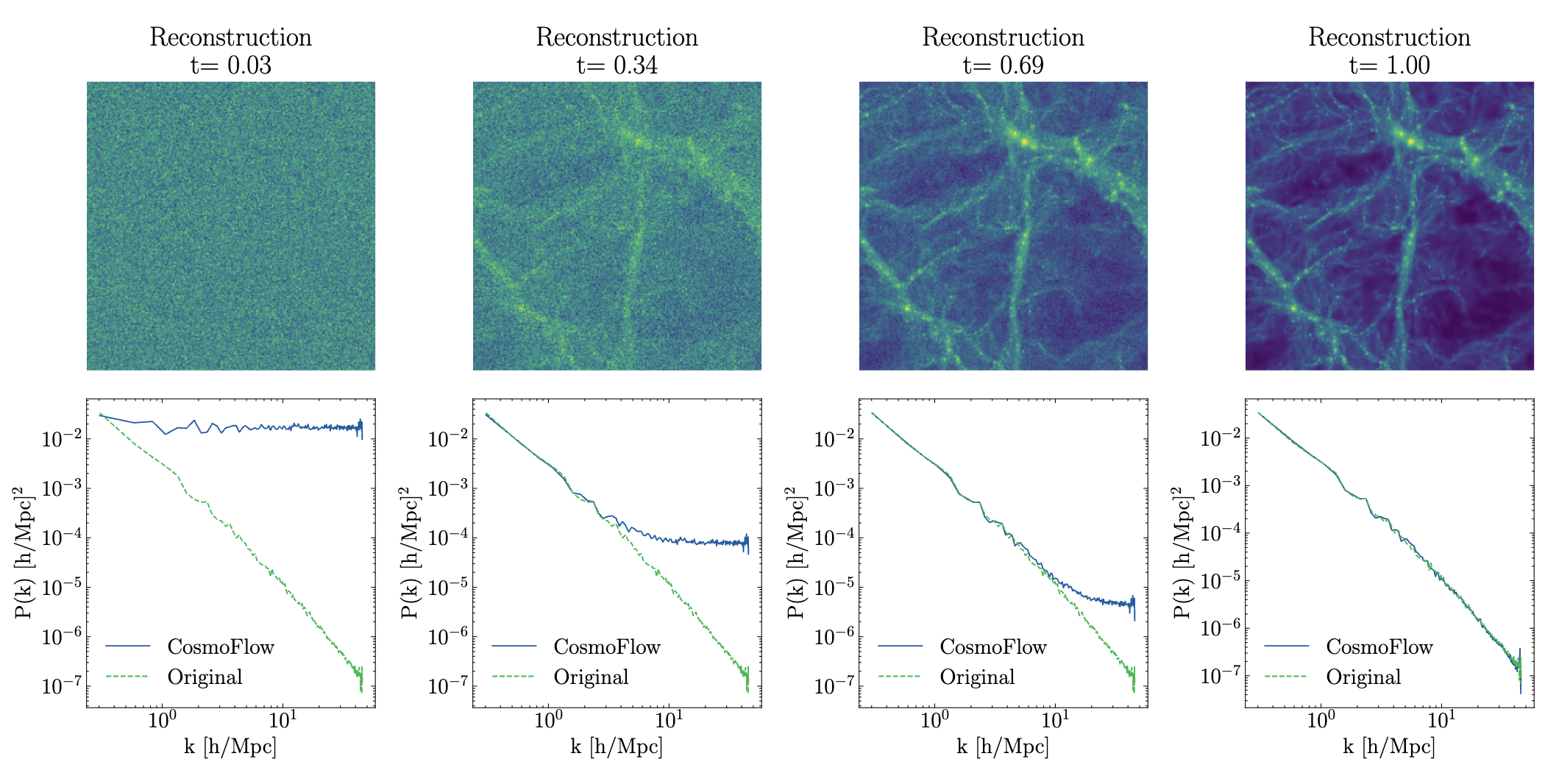
Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

["CosmoFlow: Scale-Aware Representation Learning for Cosmology with Flow Matching" Kannan et al (in prep)]
\mathrm{R} \sim p(\theta|x)
\mathrm{F} \sim \hat{p}(\theta|x)

Real or Fake?

How good is my generative model?

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Mean relative velocity

k Nearest neighbours

Pair separation

Pair separation

Varying cosmological parameters

Physics as a testing ground: Well-understood summary statistics enable rigorous validation of generative models

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Reproducing summary statistics

Has my model learned the underlying density?

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

["Generalization in diffusion models arises from geometry-adaptive harmonic representations" Kadkhodaie et al (2024)]

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

Generate = Understand?

 

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

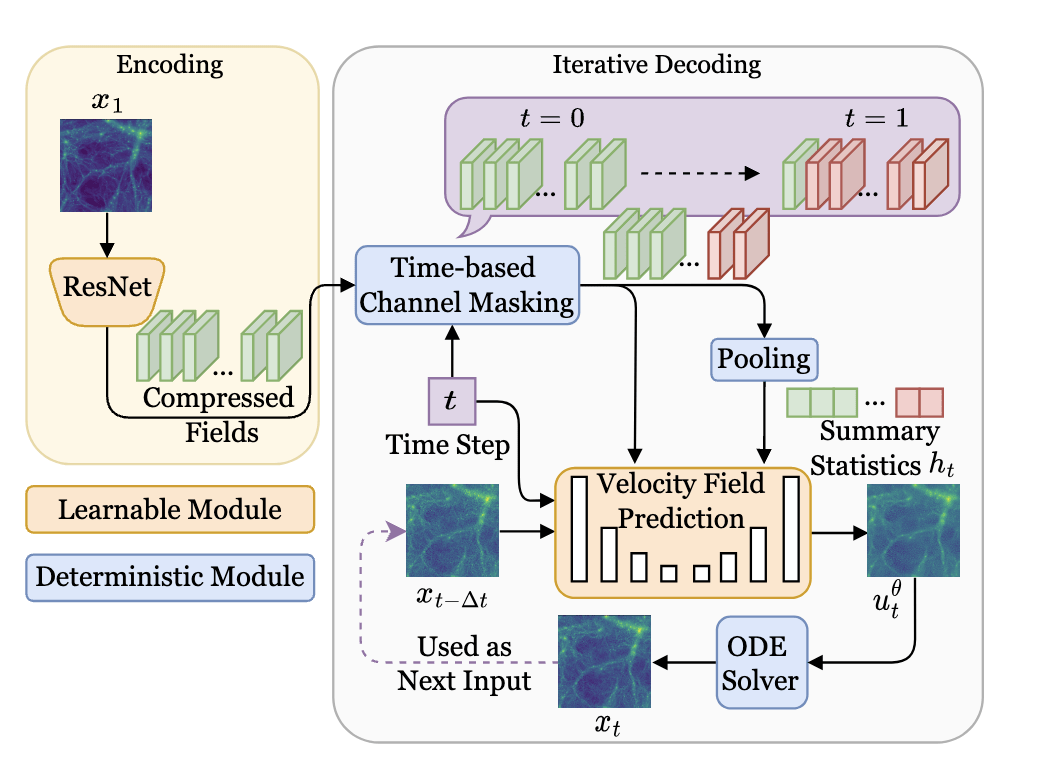
["CosmoFlow: Scale-Aware Representation Learning for Cosmology with Flow Matching" Kannan et al (in prep)]

Generate = Understand?

 

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

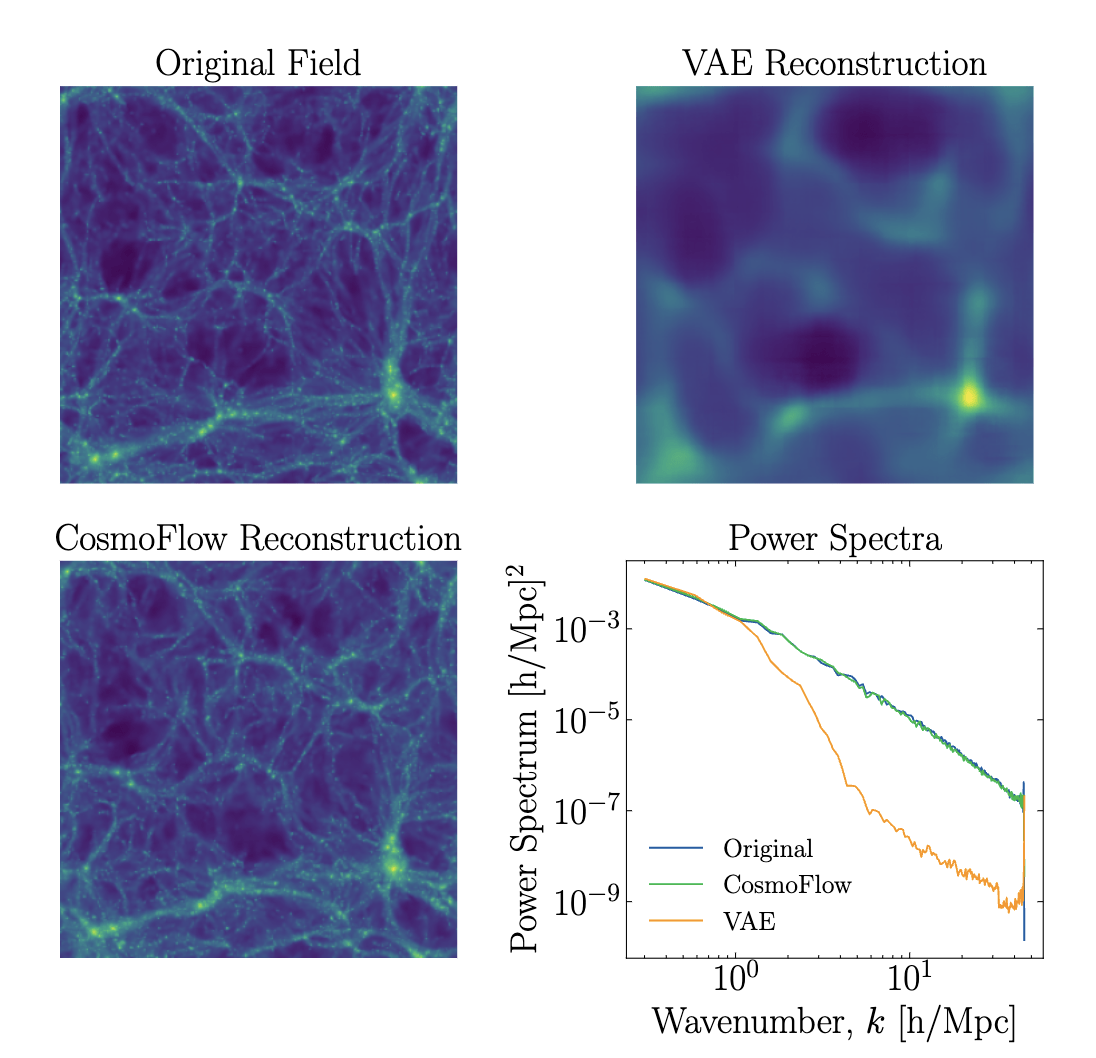
["CosmoFlow: Scale-Aware Representation Learning for Cosmology with Flow Matching" Kannan et al (in prep)]

Tutorial

x_0

Gaussian

MNIST 

x_1

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

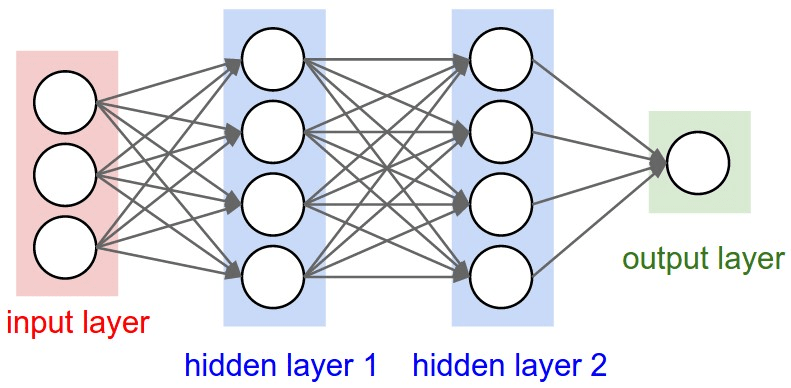
import flax.linen as nn

class MLP(nn.Module):
    @nn.compact
    def __call__(self, x):
      	# Linear
        x = nn.Dense(features=64)(x)
        # Non-linearity
        x = nn.silu(x)
        # Linear
        x = nn.Dense(features=64)(x)
        # Non-linearity
        x = nn.silu(x)
        # Linear
        x = nn.Dense(features=2)(x)
        return x

model = MLP()

Jax Models

import jax.numpy as jnp

example_input = jnp.ones((1,4))
params = model.init(jax.random.PRNGKey(0), example_input) 
y = model.apply(params, example_input)

Architecture

Parameters

Call

Carolina Cuesta-Lazaro IAIFI/MIT - From Zero to Generative

References

cuestalz@mit.edu

From zero to generative - MIT/CfA Summer students - 2025

By carol cuesta

From zero to generative - MIT/CfA Summer students - 2025

  • 57

More from carol cuesta