Haskell
Part 3


Recap
:t <something>
:i <something>
GHC.IO
Defining stuff
let count = 1
let add x y = x + y
let v = 2 :: Int
let h = 3 :: FloatCalling functions
add 1 2
let add10 = add 10Basic Types
'c', False,"123", 1, [1,2,3], (1,True)
Lists
Can only be of single type
(++), (:), (!!)
head, tail, last, init
length, reverse, drop, take
sum, product, minimum, maximum, elem
Ranges
[1..20], ['a'..'z'], ['V'..'Z']
[1,2..20]
cycle, repeat, replicate,
List comprehensions
[x*2 | x <- [1..10], x*2 >= 12] [ x*y | x <- [2,5,10], y <- [8,10,11]] [x*2 | x <- [1..10]] Tuples
fst, snd, zip
In Haskell
Everything has a type
(+1) :: Int -> Int(+) :: Int -> Int -> IntTypeclasses
Things that defines behaviour
Not like classes
Think of them as interfaces
instead.
Example
:t (==)== is actually a function.
So is +, -, /, * and almost all operators.
The Eq Typeclass
for types that support equality testing.
Almost all of the standard types
(==) :: (Eq a) => a -> a -> Bool Everything before => is called a class constraint
The (==) function takes two values of the same type and returns a Bool.
The type of the two types must be a member of the the Eq typeclass,
The elem function
has the type
elem :: (Eq a) => a -> [a] -> Boolbecause it uses the (==) function over a list to check whether it contains the value we are looking for
Example
data Day = Mon | Tue | Wed | Thu | Fri | Sat | Sun
deriving (Eq)Mon == FriFri /= WedThe Ord Typeclass
for types that have ordering
(<) :: (Ord a) => a -> a -> Bool :t (<)Example
data Day = Mon | Tue | Wed | Thu | Fri | Sat | Sun
deriving (Eq, Ord)Mon > FriFri > WedThe Enum Typeclass
for types that are sequentially ordered
allows you to use them in list ranges
Example
data Day = Mon | Tue | Wed | Thu | Fri | Sat | Sun
deriving (Enum)[Mon..Fri]succ Fripred FriThe Show Typeclass
Example
data Day = Mon | Tue | Wed | Thu | Fri | Sat | Sun
deriving (Show)show FriThe Read Typeclass
Example
data Day = Mon | Tue | Wed | Thu | Fri | Sat | Sun
deriving (Read)read "Fri"The Num Typeclass
for types that act like numbers
Type of a number
13 :: (Num t) => t :t 13Whole numbers can act like
any type that's a member of Num
:t 13 :: Int:t 13 :: Float:t 13 :: Double:t (+)(+) :: (Num a) => a -> a -> a So you can add numbers like so:
(1 :: Double) + (3 :: Int)Functor
is just another typeclass
What behaviour does it define?
Context
A value can be wrapped in a context
The Maybe type
data Maybe a = Nothing | Just a2 -- a normal value
Just 2 -- a type of context wrapping a value
Nothing -- an empty type of contextNothing :: Maybe a
Just :: a -> Maybe a
When a value is wrapped in a context (eg a list, or maybe)
You can't apply a normal function to it.
fmap
fmap knows how to apply a function to a value in a context
> fmap (+3) (Just 2)
Just 5> fmap (+3) Nothing
Nothingclass Functor f where
fmap :: (a -> b) -> f a -> f bTo make datatype f a functor
You'll need to implement this function for your data type
Pattern Matching
isOne :: Int -> Bool
isOne 1 = True
isOne _ = Falsepow :: Int -> Int -> Int
pow _ 0 = 1
pow a b = a^binstance Functor Maybe where
fmap function (Just x) = Just (function x)
fmap function Nothing = Nothing 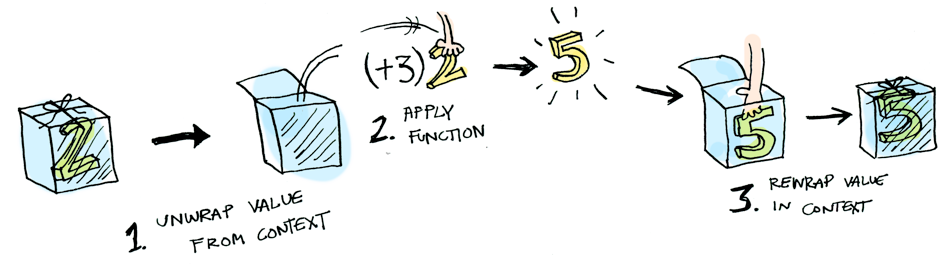
fmap (+3) (Just 2)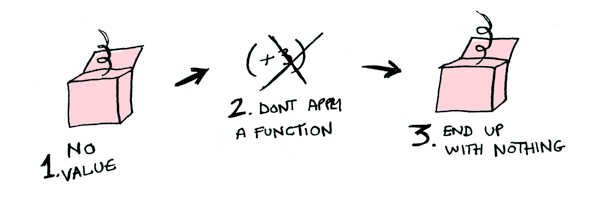
fmap (+3) NothingAnother Example
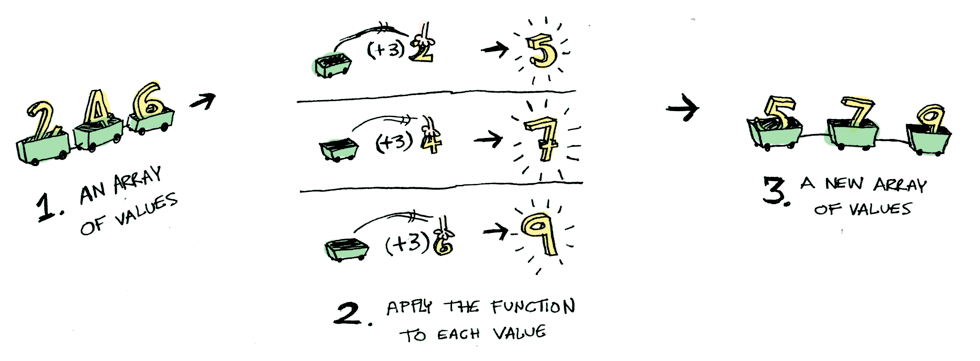
fmap (+3) [2,4,6]instance Functor [] where
fmap = mapThat's all for this week
Questions?
That's all folks